2017-2018学年山西省太原市第五中学高二上学期10月阶段性检测数学（文）试题 8页

太原五中2017-2018学年度第一学期阶段性检测 高 二 数 学（文）‎ 命题人、校对人：吕兆鹏 禹海青（2017.10）‎ ‎ ‎ 一、 选择题(本大题共12小题，每小题3分，共36分)‎ 1. 下列判断错误的是（ ）‎ A. 平行于同一直线的两条直线互相平行；‎ B. 平行于同一平面的两个平面互相平行；‎ C. 经过两条异面直线中的一条，有且仅有一个平面与另一条直线平行；‎ D. 垂直同一平面的两个平面互相平行 2. 分别和两条异面直线都相交的两条直线的位置关系是（ ）‎ A. ‎ 异面 B. 相交 C. 平行 D. 异面或相交 3. 已知正方体ABCD-A1B1C1D1的棱长为，点B1到平面A1C1B的距离为( ) ‎ A. 错误！未指定书签。 B. C. D. ‎ ‎4.如图1-4所示，是某一容器的三视图，现向容器中匀速注水，容器中水面的高度h随时间t变化的可能图象是（ ）‎ A B C D 图1-4‎ 正视图 ‎·‎ ‎ ‎ 侧视图 俯视图 ‎5.一个几何体的三视图如图1-5所示，则该几何体的表面积为（ ）‎ A. 6+8 B. 12+7 C. 12+8 D. 18+2 x¢‎ y¢‎ o¢‎ A¢‎ B¢‎ C¢‎ 图1-7‎ ‎1‎ ‎3‎ ‎2‎ ‎2‎ 正视图 侧视图 俯视图 图1-5‎ ‎6. 在三棱锥S--ABC中，SB ^ AC ，SB= AC=1 ，E、F分别是SC和AB的中点，则EF的长为（ ）‎ A. 1 B. C. D. ‎7. 如图1-7是一水平放置的梯形OABC按“斜二测画法”得到的直观图，其面积为2，则原梯形OABC的面积为( )‎ A. 2 B. 4 C. 6 D. 8 ‎ ‎8. 若一圆锥与一球的体积相等，且此圆锥底面半径与此球的直径相等，则此圆锥侧面积与此球的表面积之比为（ ）‎ A. : 2 B. : 2 C. : 2 D. 3 : 2 ‎ ‎9.在正方体ABCD--A1B1C1D1中，下列结论正确的是（ ）‎ A. 直线A1B与直线AC所成的角是450；B. 直线A1B与平面ABCD所成的角是300；‎ C. 二面角A1--BC--A的大小是600； D. 直线A1B与平面A1B1CD所成的角是300.‎ ‎10. 若两异面直线a,b所成的角为700，过空间内一点P作与直线a ,b 所成角均是700的直线，则所作直线共有（ ）条.‎ A. 1 B. 2 C. 3 D. 4 ‎ ‎11. 已知直线^平面α，直线mÌ平面β，下列四个命题中正确的是（ ）‎ ‎① 若α // β ，则 ^ m ； ② 若α ^ β， 则// m ； ‎ ‎③ 若// m ，则 α ^ β； ④ 若^ m，则 α // β ‎ A. ② B. ①③ C. ①③④ D. ①②③④ ‎ ‎12. 已知球O的直径SC= 4，A 、B是该球面上的两点，且AB=2，ÐASC=300，ÐBSC=450，则三棱锥S-ABC的体积为（ ）‎ A. B. C. D. 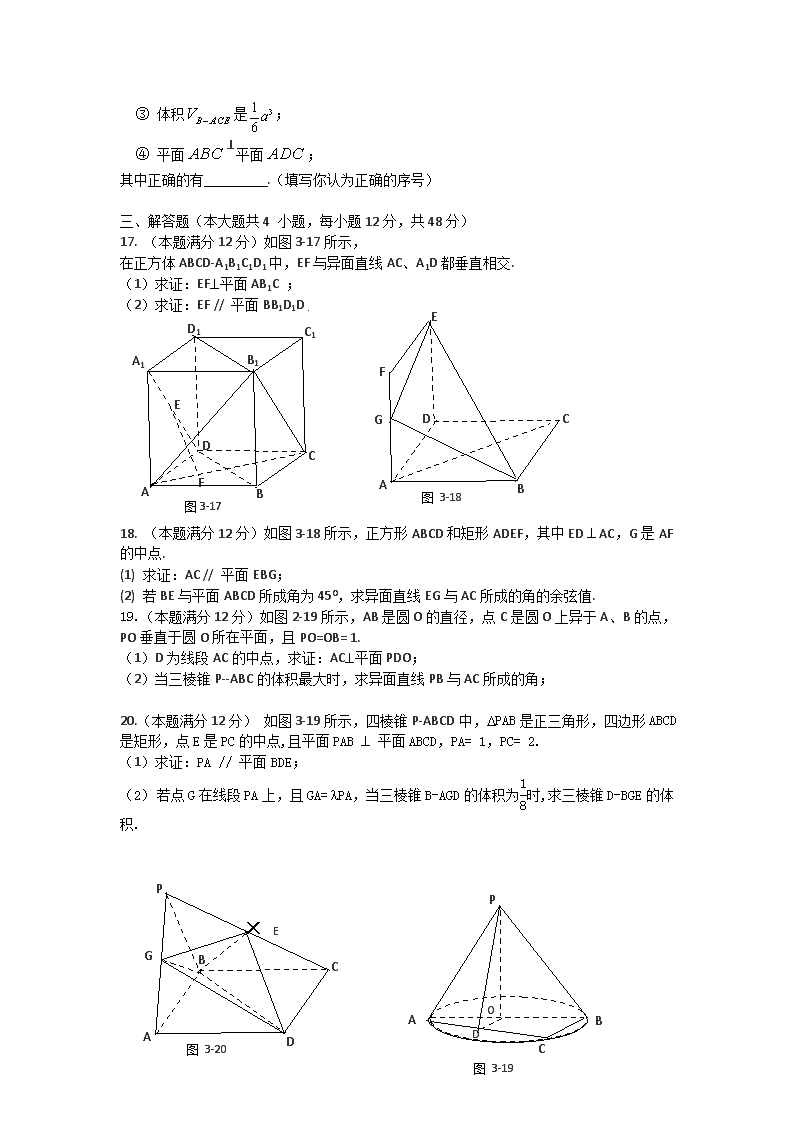‎ 二、填空题（本大题共4 小题，每小题4分，共16分）‎ ‎13.已知底面边长为,各侧面均为直角三角形的正三棱锥P-ABC的四个顶点都在同一球面上，则此球的体积为 ‎ ‎14.半径为R的一个半圆卷成一个圆锥，则其表面积为 ‎ ‎15.已知在正四面体ABCD中，E是AD的中点，则CE与平面BCD所成角的 正弦值为 ‎ A ‎ D ‎ C ‎ B ‎ E ‎ 图2-16 ‎ ‎16..如图，正方形的边长为，已知，‎ 将沿边折起，折起后点在平面上的 射影为点，则翻折后的几何体中有如下描述：‎ ‎① 与所成角的正切值是； ‎ ‎② ∥；‎ ‎③ 体积是； ‎ ‎④ 平面⊥平面；‎ 其中正确的有 .（填写你认为正确的序号）‎ 三、 解答题（本大题共4 小题，每小题12分，共48分）‎ 17. ‎（本题满分12分）如图3-17所示，‎ 在正方体ABCD-A1B1C1D1中，EF与异面直线AC、A1D都垂直相交.‎ （1） 求证：EF^平面AB1C ；‎ B1‎ A B C D A1‎ C1‎ D1‎ E F 图3-17‎ A B C D E F G 图 3-18‎ （2） 求证：EF // 平面BB1D1D . ‎ 18. ‎（本题满分12分）如图3-18所示，正方形ABCD和矩形ADEF，其中ED ^ AC，G是AF的中点.‎ (1) 求证：AC // 平面EBG；‎ (2) 若BE与平面ABCD所成角为450，求异面直线EG与AC所成的角的余弦值. ‎ ‎19.（本题满分12分）如图2-19所示，AB是圆O的直径，点C是圆O上异于A、B的点，PO垂直于圆O所在平面，且PO=OB= 1.‎ ‎（1）D为线段AC的中点，求证：AC^平面PDO；‎ ‎（2）当三棱锥P--ABC的体积最大时，求异面直线PB与AC所成的角；‎ ‎20.（本题满分12分） 如图3-19所示，四棱锥P-ABCD中，DPAB是正三角形，四边形ABCD是矩形，点E是PC的中点,且平面PAB ^ 平面ABCD，PA= 1，PC= 2.‎ ‎（1）求证：PA // 平面BDE；‎ ‎（2） 若点G在线段PA上，且GA= lPA，当三棱锥B-AGD的体积为时,求三棱锥D-BGE的体积.‎ A B C D ‎× E P G 图 3-20‎ P A B O C ‎ D ‎ 图 3-19‎ ‎ （2017--2018年度）高 二 数 学(文) 参考答案 ‎ 一、 DDCAC CBADD BC ‎ 二、 ‎13. ； 14. ； 15. ；16. ①③④ ‎ 三、 解答题 ‎17. 证明：思路提示：‎ （1） EF ^ AC，EF^ B1C ÞEF^平面AB1C；‎ （2） 只证：BD1^平面AB1C ，由（1）知：‎ A B C D E F G 图 3-18‎ H EF^平面AB1C ， EF//BD1 Þ EF//平面BB1D1D . ‎ B1‎ A B C D A1‎ C1‎ D1‎ E F 图3-17‎ ‎18. 解：思路提示：‎ ‎（1）延长EG与DA并交于点H，由于G为AF的中点，不难证明：A为HD的中点，AH 与BC 平行且相等，‎ Þ AC//HB Þ AC // 平面EBG；‎ （2） 令BC= 2 ，因为：DE^DA，DE^AC ，DA与AC相交，Þ DE^平面ABCD Þ BD是BE是平面ABCD内的射影Þ ÐEBD是BE与平面ABCD所成的角，Þ ÐEBD =450 Þ DE= BD= 2,由（1）知：ÐEHB 是异面直线EG与AC所成的角，在DEHB中，由余弦定理P O B C A C¢‎ 图3-19‎ 不难求得：cosÐEBD= .‎ ‎19. P A B O C ‎ D ‎ 图 3-20‎ P A B O C ‎ D ‎ 图 3-20‎ P A B O C ‎ D ‎ 图 3-20‎ P A B O C ‎ D ‎ 图 3-20‎ 解： 思路提示：‎ ‎（1）AC ^ OD，AC ^ PO Þ AC^平面PDO；‎ ‎（2）由题可知：PO=OB= 1. DABC为R tD 令AC= a, BC - b , 则a2+b2 = 4 ‎ VP--ABC = SDABC ×PO = ab ≤ ´ = ´ = 当且仅当a= b= 时，三棱锥P--ABC的体积取到最大值，‎ ‎ A C= BC = , 在圆O内作正方形ACBC¢ ,则AC //BC¢ , ‎ ‎ÐPBC¢就是异面直线PB与AC所成的角,PB= PC¢ = BC¢ = ， DPBC¢为正三角形， ÐPBC¢ = 600 , ‎ ‎ 异面直线直线PB与AC所成的角为600 . ‎ ‎20.解： 思路提示：‎ ‎（1）连AC利用三角形中位线可证明（略）‎ ‎（2）过P作PF^ AB， 垂足为F， ‎ 因为DPAB是正三角形，平面PAB^平面ABCD，‎ 所以：PF^平面ABCD，且F为中点，连FC，‎ P A B C D E G 图 3-20‎ F ‎ PF^ FC，PF= ,令BC = b ,‎ 在RtDPFC中，PC2 = PF2+FC 2 ，‎ 即：22 = ()2 + ( )2 + b2 , ‎ 解得：b= ,‎ 又VB-ADG = VG-ADB , hG = l ,‎ ‎ VG-ADB = SDADB hG = ×(×1×)×l = ,‎ 解得: l = ，G为PA的中点，如图示连PD 方法一：（分割法）则有：VP-ABCD = VG-ABD + VE-BDC + VP-BGE + VD-BGE + VP-DGE VP-ABCD = × 1´´ = , VG-ABD = VE-BDC = 不难证明：CB^平面PAB，E到平面PGB的距离为hE = = ‎ VP-BGE = VE-PBG = ´ ´ ´ = ‎ VP-BGE = VE-PDG = ´VC-PAB = ´ VP-ABCD = ´ ´ = .‎ VP-DGE = VE-PGD = ´VC-PAD = ´ VP-ADC =´ VP-ABCD = ‎ ‎ VD-BGE = VP-ABCD - VG-ABD - VE-BDC - VP-BGE - VP-DGE ‎ P A B C D E G 图 3-20‎ O ‎= - - - - = . ‎ 方法二：设AC与BD相交于O,连GO、EO,‎ 则四边形PGOE为平行四边形，‎ VD-BGE = 2VB-GEO , SDGOE = SDPAC ‎ ‎ VB-GEO = VB-PAC = VP-ABC = ´ VP-ABCD = ´ ´( ´ 1´´ )= ‎, VD-BGE = 2VB-GEO = 2´= . ‎