高中数学：1_3_2《直线的极坐标方程》课件（新人教a版选修4-4） 16页

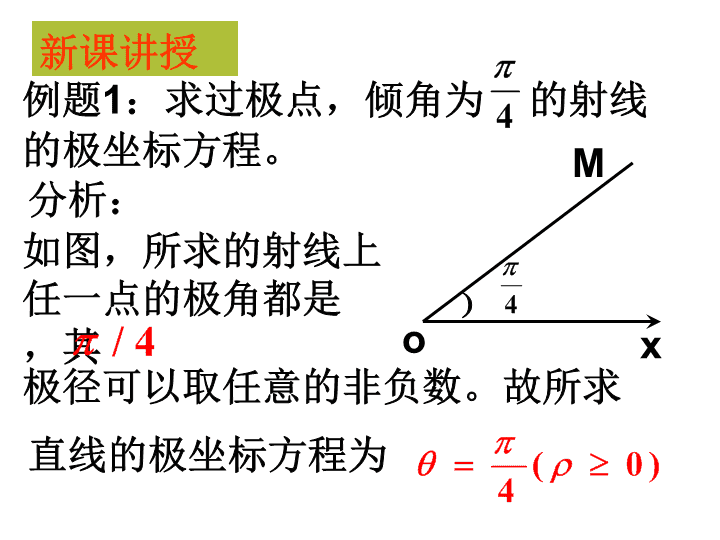
§1.3.2 直线的极坐标方程 答：与直角坐标系里的情况一样，求曲线的极坐标方程就是找出曲线上动点Ｐ的坐标  与  之间的关系，然后列出方程  (,)=0 ，再化简并讨论。 怎样求曲线的极坐标方程？ 复习引入： 例题 1 ：求过极点，倾角为 的射线的极坐标方程。 o M x ﹚ 分析： 如图，所求的射线上任一点的极角都是 ，其 极径可以取任意的非负数。故所求 直线的极坐标方程为 新课讲授 1 、求过极点，倾角为 的射线的极坐标方程。 易得 思考： 2 、求过极点，倾角为 的直线的极坐标方程。 和前面的直角坐标系里直线方程的表示形式比较起来，极坐标系里的直线表示起来很不方便，要用两条射线组合而成。原因在哪？ 为了弥补这个不足，可以考虑允许极径可以取全体实数。则上面的直线的极坐标方程可以表示为 或 例题 2 、 求过点 A(a,0)(a>0) ，且垂直于极轴的直线 L 的极坐标方程。 解：如图，设点 为直线 L 上除点 A 外的任意一点，连接 OM o x ﹚ A M 在 中有 即 可以验证，点 A 的坐标也满足上式。 求直线的极坐标方程步骤 1 、根据题意画出草图； 2 、设点 是直线上任意一点； 3 、连接 MO ； 4 、根据几何条件建立关于 的方 程，并化简； 5 、检验并确认所得的方程即为所求。 练习： 设点 P 的极坐标为 A ，直线 过点 P 且与极轴所成的角为 , 求直线 的极坐标方程。 解：如图，设点 为直线 上异于的点 连接 OM ， ﹚ o M x A 在 中有 即 显然 A 点也满足上方程。 小结：直线的几种极坐标方程 1 、过极点 2 、过某个定点，且垂直于极轴 3 、过某个定点，且与极轴成一定 的角度 O H M A A 、两条相交的直线 B 、两条射线 C 、一条直线 D 、一条射线 ( ) B ( ) C ( ) B O X A B