2020届二轮复习两角差的余弦公式课件（14张）（全国通用） 14页

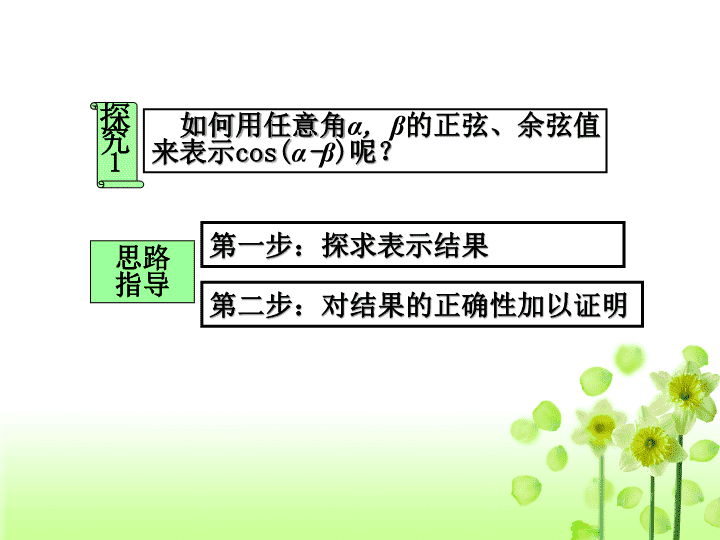
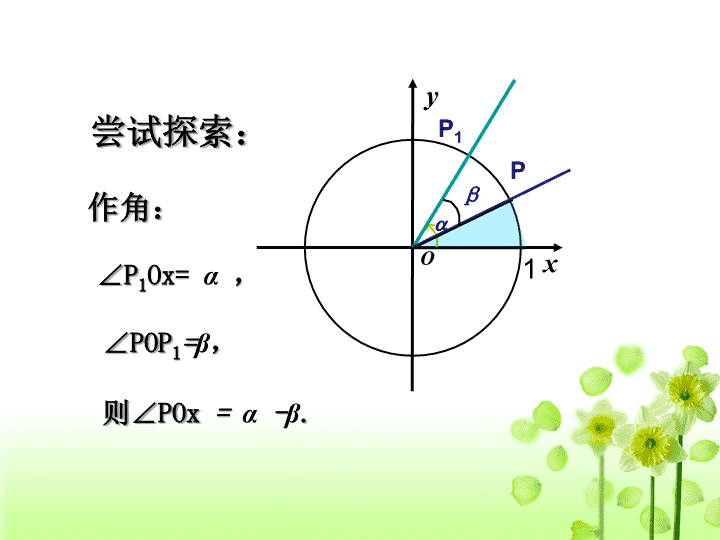
如何用任意角 α , β 的正弦、余弦值 来表示 cos( α - β ) 呢？ 探究 1 第一步：探求表示结果 思路 指导 第二步：对结果的正确性加以证明 问题 1: 你认为 cos( α - β )= cos α - cos β 成立吗 ? 议一议 ： 问题 2 涉及的是三角函数的问题， 是否可以联系单位圆上的三角函 数线解决？ 问题 2: 如何用任意角 α 、 β 正弦余弦值来表示 cos ( α - β ）呢 ? 尝试探索： O x y 作角： P 1  ∠ P 1 Ox= α ， β P ∠ POP 1 = β ， 则∠ POx = α - β . 1 O x y P 找线 : P 1 cos( α -β ) cos α cos β +sin α sin β A B AB ⊥ x 轴 ∠ PAB =∠ P 1 Ox = α CP ⊥ AB C β  CP OB cos α OA +sin α AP · · M OM 1 O x y P 1 P M A B C 即 : 思考： 以上结果为 α 、 β 、 α - β 均为锐角，且 α > β 的情况下得到的，此式是否对任意角都成立呢？ β  cos ( α - β )= cos α cos β + sin α sin β 1 探究 2 对任意 α 、 β ，如何证明它的正确性？ 议一议： 看能否用向量的知识进行证明？ 结合向量的数量积的定义和向量的工具性， y O x A B α β 问题 3 ： ① 结合图形，思考应选用哪几个向量？ ② 怎样用向量数量积的运算和定义得到结果？ OA =( cos α , sin α ), 以下推导是否严谨？若不 严谨 ，请作出补充。 OB =(cos β ,sin β ). y O x A B α β 如图： 在平面直角坐标系 x O y 内作单位圆 O ，以 Ox 为始边作角 α 、 β ， 它们的终边与单位圆的交点分别为 A 、 B ，则 由向量数量积的定义，有 由向量数量积的坐标表示，有 　　　　　　　　　 于是 当 α - β 为任意角时，由诱导公式，总可以找到一个角 ∈ [0,2  ), 使 cos  = cos( α - β ). 于是，对于任意角 α ， β 都有 cos( α - β )=cos α cos β +sin α sin β 称为差角的余弦公式 . 简记为 C （ α - β ） . 则 OA · OB = cos(2  -  )=cos( α - β ). y α O x A B β y O x A B α β ① 若  ∈ [0, ],  则 OA · OB =cos  = cos( α - β ). 2 -  则 2 -  ∈ (0,  ） ,  ② 若  ∈ (  ,2  ） , 想一想： 公式有何特点？你如何记忆？ 一、平面内两点间距离公式的引入 x . P 1 (x 1 ,y 1 ) y o . P 2 (x 2 ,y 2 ) M 1 M 2 N 1 N 2 (0,y 1 ) (0,y 2 ) Q 　 P 1 Q = M 1 M 2 QP 2 = N 1 N 2 由勾股定理得： 　　　　由此可得平面内 P 1 (x 1 ,y 1 ), P 2 (x 2 ,y 2 ) (x 1 ,0) (x 2 ,0) 想一想，数轴上两点间的距离是如何求得的？ A B O x x 1 x 2 AB= │x 2 -x 1 │ =│x 2 -x 1 │ =│y 2 -y 1 │ 两点间的距离公式： 二、两角和的余弦公式的推导 x y o P 1 P 2 α β P 4 P 3 -β (1,0) (cosα,sinα) (cos(α+β),sin(α+β)) (cos(-β),sin(-β)) 观察：图中还有哪些相等关系？ 二、两角和的余弦公式的推导 x o P 1 P 2 α β P 4 P 3 -β (1,0) (cosα,sinα) (cos(α+β),sin(α+β)) (cos(-β),sin(-β)) y 由两点间的距离公式可得： P 1 P 3 = P 2 P 4 由 P 1 P 3 = P 2 P 4 ，得 展开并整理得： 即： 应用 分析：怎样把 15° 表示成两个特殊角的差？ 变式 : 求 sin 75° 的值 . 解： 1: 已知四个单角函数值求差角的余弦。 例 1 ，利用差角余弦公式求 cos15° 的值 .