河南省郑州市2020届高三高中毕业年级质量预测数学（理）试题 8页

‎2020 年高中毕业年级第二次质量预测 理科数学试题卷 注意事项：‎ 1. 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．‎ 2. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号．回答非选择题时，将答案写在答题卡上．写 在本试卷上无效．‎ 3. 考试结束后，将本试卷和答题卡一并交回．‎ 一、选择题：本 大题共 12 小题 ，每小题 5 分，共60 分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 已知集合 A = {x｜a +l≤x≤3a- 5} , B = {x|3<工 < 22} , 且 A Ç B = A , 则实数 a 的取值范围是 A.(-¥,9] B.(-¥,9) C.[2,9] D.(2,9)‎ ‎2.已知复数z=(其中i是虚数单位，满足i2=-1)，则 z 的共轭复数是 A. 1-2i B. 1 +2i C. -1-2i 　　　　D. -1+2i ‎3.郑州市2019年各月的平均气温(°C)数据的茎叶图如下： 则这组数据的中位数是 A. ‎20‎ B. ‎21‎ C. 20. 5‎ D. 23‎ ‎ ‎ 1. 圆(x + 2)2 + (y-12)2 = 4 关于直线 x - y +8=0对称的圆的方程为 A. (x+3)2 + (y+2)2 =4 B. (x+4)2+(y-6)2=4‎ C.(x-4)2+(y-6)2=4 D. (x+6)2+(y+4)2=4‎ 2. 在边长为 30 米的正六边形广场正上空悬挂一个照明光源，已知这个光源发出的光线过旋转轴的截面是一个等腰直角三角形，要使整个广场都照明，光源悬挂的高度至少为 A. 30 米 B. 20 米 C. 15米 D. 15 米 3. 若aÎ(,p), 2cos2a= sin(-a)，则 sin2a 的值为 A.- ‎B. ‎C. - ‎D. 4. 在如图所示的程序框图中，若输出的值是4 , 则输入的 x 的取值范围是 A. (2, 十¥) B. (2, 4] C. (4, 10] D. 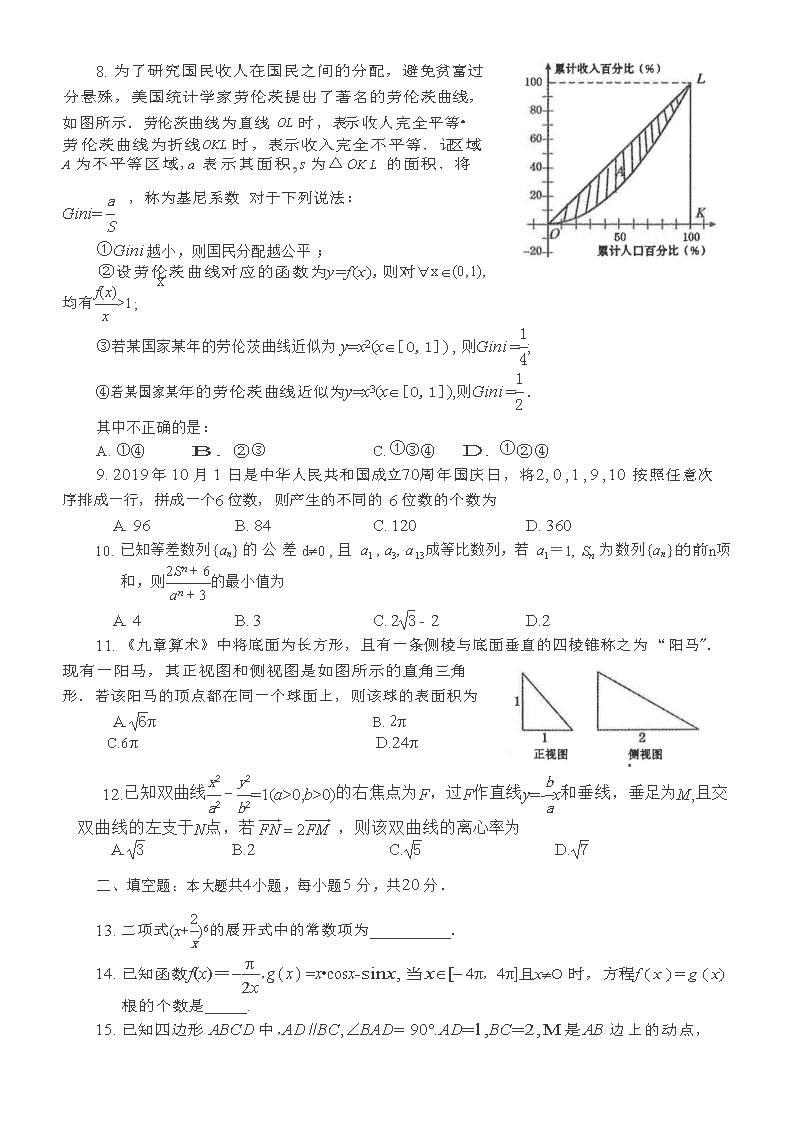(4,+ ¥)‎ 1. 为了研究国民收人在国民之间的分配，避免贫富过 分悬殊，美国统计学家劳伦茨提出了著名的劳伦茨曲线， ‎ 如图所示．劳伦茨曲线为直线 OL 时，表示收人完全平等· ‎ 劳伦茨曲线为折线 OKL 时，表示收入完全不平等．记区域 ‎ A 为不平等区域，a 表示其面积,s 为△OK L 的面积．将 ‎‎ Gini= ‎‎ ‎，称为基尼系数 对于下列说法：‎ ‎①Gini 越小，则国民分配越公平；‎ ‎②设劳伦茨曲线对应的函数为y=f(x),则对"xÎX (0,1),‎ 均有>1;‎ ‎③若某国家某年的劳伦茨曲线近似为y=x2(xÎ[0,1]) , 则Gini =;‎ ‎④若某国家某年的劳伦茨曲线近似为y=x3(xÎ[0,1]),则Gini = .‎ 其中不正确的是：‎ A. ①④ B. ②③ C. ①③④ D. ①② ④‎ 1. ‎2019 年 10 月 1 日是中华人民共和国成立70周年国庆日，将2, 0 , 1 , 9 , 10 按照任意次序排成一行，拼成一个6 位数，则产生的不同的 6 位数的个数为 A. 96 B. 84 C. 120 D. 360‎ 2. 已知等差数列{an} 的 公 差 d¹0 , 且 a1 , a3, a 13成等比数列，若 a 1 = 1, Sn 为数列{an }的前n项和，则的最小值为 A. 4 B. 3 C. 2 - 2 D.2‎ 2. ‎《九章算术》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马". 现有一阳马，其正视图和侧视图是如图所示的直角三角 形．若该阳马的顶点都在同一个球面上，则该球的表面积为 A.p B. 2p ‎ C.6p D.24p ‎12.已知双曲线=1(a>0,b>0)的右焦点为F，过F作直线y=-x和垂线，垂足为M,且交双曲线的左支于N点，若 ，则该双曲线的离心率为 A. B.2 C. D. 二、填空题：本大题共4小题，每小题5 分，共20 分．‎ 13. 二项式(x+)6的展开式中的常数项为　　　　　．‎ 14. 已知函数f(x)＝-， g ( x ) =x•cosx-sinx, 当xÎ [- 4p，4p]且x¹O 时，方程f ( x ) = g ( x) 根的个数是 .‎ 15. 已知四边形 ABCD 中，AD //BC, ÐBAD= 90°. AD=l ,BC=2 ,M是AB 边上的动点，则｜｜｜｜ 的最小值为　　　　　　．‎ ‎16.设函数 的图象上存在两点 P，Q, 使得△POQ 是以 O 为直角顶 点的直角三角形（其中 0 为坐标原点），且斜边的中点恰好在 y 轴上，则实数 m 的取值 范围是　　　　　　　　　　．‎ 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第17～21 题为必考 题，每个试题考生 都必须作答．第22、23 题为选考题，考生根据要求作答．‎ ‎（一）必考题：共 60 分 ‎17. (12 分）‎ 巳知数列{an}为公差不为零的等差数列，S7=77,且满足a112=a1•a61.‎ ‎(I) 求数列{ an} 的通项公式 ；‎ ‎( II ) 若 数 列 { bn.}满足 , 且 ,求数列{bn}的前 n 项和 Tn. ‎ ‎18. (1 2 分）‎ 由团中央学校部、全国学联秘书处、中国青年报社共同举办的 2018 年度全国“最美中学生“寻访活动结果出炉啦， 此项活动于 2018 年 6 月启 动，面向 全 国中学在校学生，通过投票方式寻访一批在热爱祖国、勤奋学习、热心助人、见义勇为等方面表现突出、自觉树立和践行社会主义核心价值观的“最美中学生”。现随 机抽取了 30 名学生的票数，绘成如图所示的茎叶图，若规定票数在 65 票以上（包括 65 票）定义为风华组．票数在 65 票以下（不包括 65 票）的学生定义为青春组．‎ ‎(I) 在这 30 名 学 生 中 ，青春组学生中有男生 7 人，风华组学生中有女生 12 人，试问 有没有 90%的把握认为票数分在青春组或风华组与性别有关；‎ ‎( II ) 如果用分层抽样的方法从青春组和风华组中抽取 5 人，再从 这 5 人中随机抽取 2‎ 人 ，那么至 少有 1 人 在青春组的概率是多少？‎ ‎（III）用样本估计总体，把频率作为概率，若从该地区所有的中学（人数很多）中随机选取 ‎4 人，用x表示所选 4 人中青春组的人数，试写出x的 分 布列，并求出 x 的 数 学期 望．‎ ‎19. (1 2 分）‎ 如图，四边形 ABCD 是矩形，沿对角线 AC 将△ACD 折起，使得点 D 在平面ABC 内的射影恰好落在边AB 上．‎ ‎( I ) 求证：平面 ABD^平面 BCD;‎ ‎（II )当= 2 时，求二 面角 D- AC- B 的余弦值 ‎ i:Q A二 C ‎20. (12 分）‎ 在平面直角坐标系 xOy 内，动点 A 到定点F ( 3, 0) 的距离与 A 到定直线x = 4 距离之比为．‎ ‎( I ) 求动点 A 的轨迹C 的方程；‎ ‎4‎ ‎( II )设点 M , N 是轨迹 C 上两个动点直 线 OM, ON 与轨迹 C 的另一交点分别为 P , Q, 且直线 OM,ON 的斜率之积等于— ，问四边形 MNPQ 的面积 S 是否为定值？ 请说明理由．‎ ‎21. (12 分）‎ 已知函数 ‎ ‎( I ) 当a = l 时 ，求曲线 y = 在 x = l 处的切线方程；‎ ‎(II )讨论函数 F (x ) =在 ( 0, 十oo ) 上的单调性．‎ ‎（二）选考题：共 10 分．请考生在第 22、23 题中任选一题做答，如果多做，则按 所做的第一题记分．‎ ‎22. [ 选修 4- 4: 坐标系与参数方程] (10 分）‎ 在极坐标系中，圆C 的 方程 为r = 2asinq (a > 0). 以极点为坐标原点，极轴为x 轴的正 半轴建立平面直角坐标系，设直线 l 的 参数方 程为 ( t 为参数）．‎ ‎(I) 求 圆 C 的标准方程和直线 l 的普通方程，‎ ‎(II )若直线 l 与圆 C 交于A , B 两点，且|AB| ≥ . 求实数 a 的取值范围．‎ ‎23. [ 选修 4- 5: 不等式选讲] (10 分） 已知函数 f ( x) = lx + I l - a |x- 1 |.‎ ‎( I )当 a = - 2 时，解不等式 f (x ) >5;‎ ‎( II )若 f (x )≤a |x + 3|, 求 a 的 最小值．‎ 郑州市2020年高中毕业年级第二次质量预测 理科数学 评分参考 一、 选择题 BCCCA ABBBD CC 二、填空题 ‎ 13.160； 14.8； 15.3； 16.‎ 三、解答题 ‎17.(1)设等差数列的公差为，则……………………3分 解得 ………………5分 ‎(2)由 当时，‎ ‎= …………………………8分 对也适合， ………………………9分 ‎ …………………10分 ‎ 12分 18. ‎(I)作出列联表：‎ 青春组 风华组 合计 男生 ‎7‎ ‎6‎ ‎13‎ 女生 ‎5‎ ‎12‎ ‎17‎ 合计 ‎12‎ ‎18‎ ‎30‎ ‎………………………3分 由列联表数据代入公式得，…………………5分 因为1.83<2.706，‎ 故没有90%的把握认为成绩分在青春组或风华组与性别有关. ………………………… 6分 ‎ ‎(Ⅱ) 用A表示“至少有1人在青春组”，则. …………… 8分 ‎(III)由题知，抽取的30名学生中有12名学生是青春组学生，抽取1名学生是青春组学生的概率为，那么从所有的中学生中抽取1名学生是甲组学生的概率是，又因为所取总体数量较多，抽取4名学生可以看出4次独立重复实验，于是服从二项分布.‎ ‎………………………10分 显然的取值为0，1，2，3, 4 . 且.‎ 所以得分布列为：‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 数学期望 …………………………12分 ‎19.（Ⅰ）设点在平面上的射影为点，连接，则平面，‎ ‎∴.………………………………………………………………………2分 ‎∵四边形是矩形，∴，∴平面，∴.‎ ‎………………………………………………………………………………………4分 又，所以平面，而平面，∴平面平面.‎ ‎………………………………………………………………………………………6分 ‎（Ⅱ）以点为原点，线段所在的直线为轴，线段所在的直线为轴，建立空间直角坐标系，如图所示.设，则，∴，.‎ 由（Ⅰ）知，又，∴，，‎ ‎∴，，，‎ ‎∴，∴，.………………8分 设平面的一个法向量为，‎ 则，即 不妨取，则，，∴.‎ 而平面的一个法向量为，…………………………………………10分 ‎∴.‎ 故二面角的余弦值为.…………………………………………………12分 ‎20.解(I)设，由题意，， ……………………………2分 化简得，…（3分）所以，动点的轨迹的方程为… 4分 ‎(Ⅱ)解：设，，则由斜率之积，得，………6分 ‎，因为点在椭圆上，‎ 所以化简得． …………………………8分 直线的方程为，原点到直线的距离为 所以，的面积， ‎ 根据椭圆的对称性，四边形的面积，……10分 所以，‎ ‎，所以 所以，四边形的面积为定值12． ……………………………………12分 ‎21.解析：（Ⅰ）当时，曲线 ‎ ………………………2分 时，切线的斜率为，又切线过点 所以切线方程为…………………………4分 ‎（Ⅱ），‎ ‎………5分 当时，，函数在上单调递减；………………………7分 当时，令，‎ 当时，即，，此时，函数在上单调递增;‎ 当时，即，方程有两个不等实根，‎ 所以， ‎ 此时，函数在上单调递增；在上单调递减.……………11分 综上所述，当时，的单减区间是；‎ 当时，的单减区间是，‎ 单增区间是 当时，单增区间是.………………………12分 ‎22.（Ⅰ）C的直角坐标方程为， ………………………2分 消t得到………………………………………4分 ‎（Ⅱ）要满足弦及圆的半径为a可知只需圆心（0，a）到直线l的距离即可。由点到直线的距离公式有：…………7分 整理得：即解得：，‎ 故实数a的取值范围为……………………………………10分 ‎23.解：（Ⅰ）当a＝－2时，f(x)＝………………………3分 ‎ 由f(x)的单调性及f(－)＝f(2)＝5，‎ 得f(x)＞5的解集为{x|x＜－，或x＞2}．……………………………………5分 ‎（Ⅱ）由f(x)≤a|x＋3|得a≥ ………………………7分 由|x－1|＋|x＋3|≥2|x＋1|‎ 得≤，得a≥． ‎ ‎ 故a的最小值为． ………………………………10分