2019届二轮复习不等式学案（全国通用） 10页

‎2019年高考数学必考考点穿透性讲练 ‎05 不等式 ‎【考点突破】：‎ 一、.考纲要求;‎ ‎1.了解现实世界和日常生活中存在着大量的不等关系，了解不等式(组)的实际背景.‎ ‎2.会从实际问题的情境中抽象出一元二次不等式模型.‎ ‎3.通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.‎ ‎4.会解一元二次不等式，对给定的一元二次不等式，会设计求解的程序框图．‎ ‎5.会从实际情境中抽象出二元一次不等式组.‎ ‎6.了解二元一次不等式的几何意义，能用平面区域表示二元一次不等式组.‎ ‎7.会从实际情境中抽象出一些简单的二元线性规划问题，并能加以解决．‎ ‎8.了解基本不等式的证明过程；会用基本不等式解决简单的最大(小)值问题．‎ 二、题型、难度：‎ 题型：主要是选择、填空题，分值一般在10分左右，难度中等。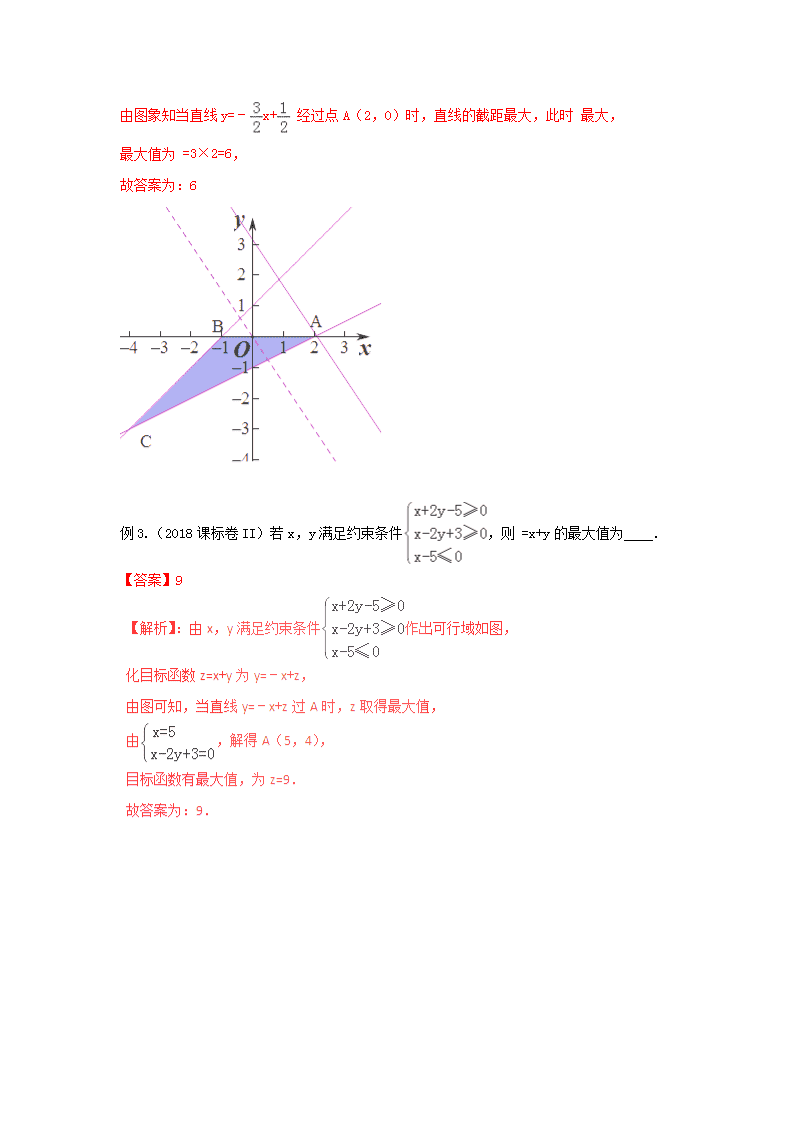‎ 三、高考真题再现：‎ 例1.（2018天津卷）已知a=log2e，b=ln2，c=log，则a，b，c的大小关系为（　　）‎ A．a＞b＞c B．b＞a＞c C．c＞b＞a D．c＞a＞b ‎【答案】D ‎【解析】解：a=log2e＞1，0＜b=ln2＜1，c=log=log23＞log2e=a，‎ 则a，b，c的大小关系c＞a＞b，‎ 故选：D．‎ 例2.（2018课标卷I） 若x，y满足约束条件，则 =3x+2y的最大值为　 　．‎ ‎【答案】6‎ ‎【解析】：作出不等式组对应的平面区域如图：‎ 由 =3x+2y得y=﹣x+ ，‎ 平移直线y=﹣x+ ，‎ 由图象知当直线y=﹣x+ 经过点A（2，0）时，直线的截距最大，此时 最大，‎ 最大值为 =3×2=6，‎ 故答案为：6‎ 例3.（2018课标卷II）若x，y满足约束条件，则 =x+y的最大值为　　．‎ ‎【答案】9‎ 学 ‎ 例4.（2018北京卷）若x，y满足x+1≤y≤2x，则2y﹣x的最小值是　　．‎ ‎【答案】3‎ ‎【解析】：作出不等式组对应的平面区域如图：‎ 设 =2y﹣x，则y=x+ ，‎ 平移y=x+ ，‎ 由图象知当直线y=x+ 经过点A时，‎ 直线的截距最小，此时 最小，‎ 由得，即A（1，2），‎ 此时 =2×2﹣1=3，‎ 故答案为：3‎ 例5.（2018天津卷） 已知a，b∈R，且a﹣3b+6=0，则2a+的最小值为　　．‎ ‎【答案】‎ ‎【解析】：a，b∈R，且a﹣3b+6=0，‎ 可得：3b=a+6，‎ 则2a+==≥2=，‎ 当且仅当2a=．即a=﹣3时取等号．‎ 函数的最小值为：．‎ 故答案为：．‎ 例6.（2018江苏卷）在△ABC中，角A，B，C所对的边分别为a，b，c，∠ABC=120°，∠ABC的平分线交AC于点D，且BD=1，则4a+c的最小值为　　． . ‎ ‎【答案】9‎ ‎【解析】：由题意得acsin120°=asin60°+csin60°，‎ 即ac=a+c，‎ 得+=1，‎ 得4a+c=（4a+c）（+）=++5≥2+5=4+5=9，‎ 当且仅当=，即c=2a时，取等号，‎ 故答案为：9．‎ ‎【模拟考场】‎ 一、 选择题 ‎1．若实数，则下列不等式中一定成立的是（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】对于A中，当，时不成立，所以是错误的；‎ 对于B中，取，时，不成立，所以是错误的；‎ 对于C中，取，时，不成立，所以是错误的，‎ 对于D中，由，，所以是正确的，故选D．‎ ‎2．若不等式组表示的平面区域是一个三角形，则的取值范围是（ ）‎ A． B． C． D．或 ‎【答案】C ‎【解析】画出不等式组表示的平面区域，由 解得，∴点的坐标为．结合图形可得，若不等式组 学 ‎ 表示的平面区域是一个三角形，则实数需满足，故选C．‎ ‎3. （安徽省定远重点中学2019届上学期第一次月考）已知函数的定义域是，则函数的定义域是 A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 由题意得，选C.‎ ‎4．若不等式的解集是，则的范围是（ ）‎ A． B．‎ C． D．‎ ‎【答案】A ‎【解析】由题意得不等式在上恒成立．‎ ‎①当时，不等式为，不等式恒成立．符合题意．‎ ‎②当时，由不等式恒成立得，解得． ‎ 综上，所以实数的范围是，故选A．‎ ‎5.(2018·南阳模拟)若x,y满足约束条件则(x+2)2+(y+3)2的最小值为 (　　)‎ A.1 B. C.5 D.9‎ ‎【答案】B.‎ ‎【解析】不等式组表示的可行域如图阴影部分所示,由题意可知点P(-2,-3)到直线x+y+2=0的距离为=,所以(x+2)2+(y+3)2的最小值为=.‎ ‎6. （2019届武汉部分高中高三12月联考）已知，，，则，，的大小关系是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ 因为，，，所以，故选C.‎ ‎7、（福建省长汀一中、连城一中等六校2019届高三上学期联考）若，且，则的最小值为（ ）‎ A． B． ‎2 C. 4 D．‎ ‎【答案】A ‎【解析】2a+b=4,所以,‎ ‎8．在上定义运算⊙：，则满足的实数的取值范围为（ ）‎ A． B． C． D．‎ ‎【答案】D ‎【解析】∵，∴‎ 由得，∴，‎ ‎∴满足的实数的取值范围为，故选D．‎ ‎9．（天门等三校2018届高三联考）已知三点共线，则的最小值为 A．11 B．‎10 ‎ C．6 D．4‎ ‎【答案】A ‎【解析】由已知，‎ ‎10．（荆州市2019届高三第一次八校联考）设不等式组表示的平面区域为，则（ ）‎ A．的面积是 B．内的点到轴的距离有最大值 C．点在内时，‎ D．若点，则 ‎【答案】C ‎11.（黄冈市2018届高三一月调研）若a＞b＞1,-1＜c＜0, 则( )‎ A.abc＜bac B.ac＞bc C.＜ D.b＞（）‎ ‎【答案】D ‎【解析】本题考查指数函数和对数函数的性质.由-1＜c＜0得0＜ c ＜1,又a＞b＞1,‎ ‎∴＜＜0, -＞-＞0, a＞b＞1＞0,∴-a＞-b,‎ 即b＞a.故选D.‎ ‎12.（2019届武汉部分高中高三12月联考）在平面直角坐标系中，是坐标原点，两定点 满足，由点集所表示的区域的面积是（ ）．‎ A.， B. C . D. . ‎ ‎【答案】4‎ ‎【解析】由 ＝ ＝·＝2，知cos∠AOB＝，又0≤∠AOB≤π，则∠AOB＝，又A，B是两定点，可设A(，1)，B(0,2)，P(x，y)，由＝λ＋μ，可得 ‎⇒.‎ 因为 λ ＋ μ ≤1，所以＋≤1，当 由可行域可得S0＝×2×＝，所以由对称性可知点P所表示的区域面积S＝4S0＝4‎ 一、 填空题 ‎13.（安庆市五校联盟2019届高三开学考） 已知正数满足的最小值是__________．‎ ‎【答案】‎ ‎【解析】因为，所以由题设只要求的最大值即可。画出不等式组表示的区域如图，结合图形可以看出当动直线经过点时，在上的截距最大，且，，应填答案。‎ ‎14（安徽省定远重点中学2019届上学期第一次月考）已知函数，则不等式的解集是___________．‎ ‎【答案】‎ ‎【解析】‎ 试题分析：函数，，由解得，由解得，故不等式的解集为.学- ‎ 考点：分段函数解不等式.‎ ‎15.（江苏省2018届高三百校联考 ）已知集合A＝{ x ≤1}，B＝{x log3(x＋a)≥1}，若x∈A是x∈B的必要不充分条件，实数a的取值范围—‎ ‎【答案】a≥5或a≤0.‎ ‎【解析】由≤1，得x2－x－6≥0，解得x≤－2或x≥3，故A＝{x x≤－2或x≥3} .‎ 由log3(x＋a)≥1，得x+a≥3故B＝{ ≥3－a}．‎ 由题意，可知BA，所以3－a≤－2或3－a≥3，‎ 解得a≥5或a≤0.‎ ‎16.（南京市2019届高三第一学期综合模拟试题（一）） 已知正实数满足，则的最小值为 ‎【答案】‎ ‎【解析】‎