2013届高考数学一轮复习 合情推理与演绎推理 7页

‎2013届高考一轮复习 合情推理与演绎推理 一、选择题 ‎1、如图,圆周上按顺时针方向标有1,2,3,4,5五个点.一只青蛙按顺时针方向绕圆从一个点跳到另一点.若它停在奇数点上,则下一次只能跳一个点;若停在偶数点上,则下一次跳两个点.该青蛙从5这个点跳起,经2 011次跳跃后它停留的点是( ) ‎ A.1 B‎.2 ‎C.3 D.4 ‎ ‎2、下列几种推理过程是演绎推理的是( ) ‎ A.两条直线平行,同旁内角互补,如果与是两条平行直线的同旁内角,则 ‎ B.某校高三(1)班有55人,(2)班有54人,(3)班有52人,由此得高三所有班人数均超过50人 ‎ C.由平面三角形的性质,推测空间四面体的性质 ‎ D.在数列{}中由此归纳出{}的通项公式 ‎ ‎3、下列表述正确的是( ) ‎ ‎①归纳推理是由部分到整体的推理 ②归纳推理是由一般到一般的推理 ③演绎推理是由一般到特殊的推理 ④类比推理是由特殊到一般的推理 ⑤类比推理是由特殊到特殊的推理 ‎ ‎ ‎ A.①②③ B.②③④ ‎ C.②④⑤ D.①③⑤ ‎ ‎4、已知等差数列{}的公差d=2,首项. ‎ ‎(1)求数列{}的前n项和; ‎ ‎(2)设求;并归纳出与的大小规律. ‎ ‎5、由数列1,10,100,1 000,…,猜测该数列的第n项可能是( ) ‎ A. B. ‎ C. D. 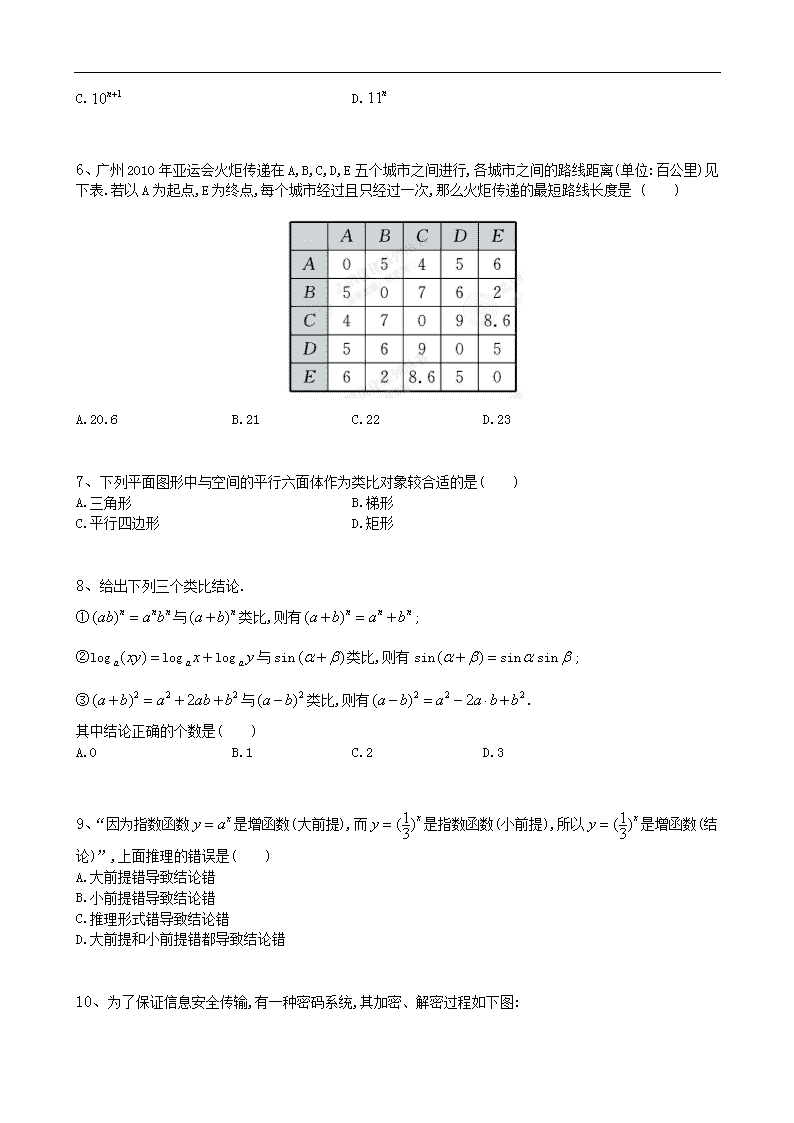‎ ‎6、广州2010年亚运会火炬传递在A,B,C,D,E五个城市之间进行,各城市之间的路线距离(单位:百公里)见下表.若以A为起点,E为终点,每个城市经过且只经过一次,那么火炬传递的最短路线长度是 ( ) ‎ A.20.6 ‎B‎.21 ‎C.22 D.23 ‎ ‎7、下列平面图形中与空间的平行六面体作为类比对象较合适的是( ) ‎ A.三角形 B.梯形 ‎ C.平行四边形 D.矩形 ‎ ‎8、给出下列三个类比结论. ‎ ‎①与类比,则有; ‎ ‎②logloglog与sin类比,则有sinsinsin; ‎ ‎③与类比,则有. ‎ 其中结论正确的个数是( ) ‎ A.0 B‎.1 ‎C.2 D.3 ‎ ‎9、“因为指数函数是增函数(大前提),而是指数函数(小前提),所以是增函数(结论)”,上面推理的错误是( ) ‎ A.大前提错导致结论错 ‎ B.小前提错导致结论错 ‎ C.推理形式错导致结论错 ‎ D.大前提和小前提错都导致结论错 ‎ ‎10、为了保证信息安全传输,有一种密码系统,其加密、解密过程如下图: ‎ 明文加密密钥密码密文发送密文解密密钥密码明文 ‎ 现在加密密钥为y=log如上所示,明文“6”通过加密后得到密文“3”,再发送,接受方通过解密密钥解密得到明文“6”.问:若接受方接到密文为“4”,则解密后得到明文为( ) ‎ A.12 B‎.13 ‎C.14 D.15 ‎ 二、填空题 ‎11、已知命题:若数列{}为等差数列,且m、N则;现已知等比数列{}N、N若类比上述结论,则可得到 . ‎ ‎12、设等差数列{}的前n项和为则成等差数列.类比以上结论有:设等比数列{}的前n项积为则 , 成等比数列. ‎ ‎13、定义集合A,B的运算:{x|或且},则= . ‎ ‎14、如图,在三棱锥O—ABC中,三条棱OA,OB,OC两两垂直,且OA>OB>OC,分别经过三条棱OA,OB,OC作一个截面平分三棱锥的体积,截面面积依次为则的大小关系为 . ‎ 三、解答题 ‎15、在△ABC中,射影定理可以表示为a=bcosC+ccosB,其中a,b,c依次为角A、B、C的对边.类比以上定理,给出空间四面体中类似性质的猜想. ‎ ‎16、等差数列{}中,公差为d,前n项的和为有如下性质: ‎ ‎(1)通项; ‎ ‎(2)若m+n=p+q,m、n、p、N则; ‎ ‎(3)若m+n=2p,则; ‎ 构成等差数列. ‎ 请类比出等比数列的有关性质. ‎ 以下是答案 一、选择题 ‎1、 A ‎ 解析:用表示青蛙第n次跳跃后所在的点数,‎ 则…,‎ 显然数列{}是一个周期为3的数列,‎ 故. ‎ ‎2、 A ‎ 解析:两条直线平行,同旁内角互补(大前提) ‎ 与是两条平行直线的同旁内角(小前提) ‎ ‎ (结论) ‎ ‎3、 D ‎ 解析:归纳推理是由部分到整体的推理,演绎推理是由一般到特殊的推理,类比推理是由特殊到特殊的推理. ‎ ‎4、 解:(1)由已知 ‎ ‎∴1)=2n+3. ‎ ‎∴. ‎ ‎2n+3)-5], ‎ ‎∴. ‎ ‎∴ ‎ ‎. ‎ ‎ ‎ ‎. ‎ 由此可知当时. ‎ 归纳猜想:当N时. ‎ ‎5、B ‎ 解析:前几项可以写成10的幂的形式,容易发现结论. ‎ ‎6、 B ‎ 解析:首先以A为起点,E为终点,每个城市经过且只经过1次的可能性有6种,即ABCDE,ABDCE,ACBDE,ACDBE,ADBCE,ADCBE,分别计算得ACDBE最短,且最短距离为21. ‎ ‎7、C ‎ 解析:因为平行六面体相对的两个面互相平行,类比平面图形,则相对的两条边互相平行. ‎ ‎8、 B ‎ 解析:③正确. ‎ ‎9、A ‎ 解析:“是增函数”这个大前提是错误的,从而导致结论错. ‎ ‎10、C ‎ 解析:∵log∴a=2, ‎ 即加密密钥为y=log ‎ 当接到的密文为4时,即log ‎ ‎∴∴x=14. ‎ 二、填空题 ‎11、 ‎ 解析:等差数列中的bn和am可以类比等比数列中的和等差数列中的bn-am可以类比等比数列中的等差数列中的可以类比等比数列中的.故. ‎ ‎12、 ‎ 解析:由于等差数列与等比数列具有类比性,且等差数列与和、差有关,等比数列与积、商有关,因此当等差数列依次每4项之和仍成等差数列时,类比到等比数列为依次每4项的积成等比数列.下面证明该结论的正确性: ‎ 设等比数列{}的公比为q,首项为 ‎ 则 ‎ ‎ ‎ ‎∴ ‎ 即 ‎ 故成等比数列. ‎ ‎13、 B ‎ 解析:如图表示的是阴影部分,‎ 设运用类比的方法可知,C 所以. ‎ ‎14、 ‎ 解析:取BC中点D,AB中点E,AC中点F, ‎ 易知面AOD,面BOF,面COE平分三棱锥的体积. ‎ ‎. ‎ 设OA=a,OB=b,OC=c,‎ 则. ‎ 同理 ‎ ‎. ‎ ‎∵a>b>c,∴. ‎ 三、解答题 ‎15、 解:如图,‎ 在四面体P—ABC中、、、S分别表示△PAB、△PBC、△PCA、△ABC的面积、、依次表示面PAB、面PBC、面PCA与底面ABC所成角的大小,我们猜想将射影定理类比推广到三维空间,其表现形式应为coscoscos. ‎ ‎16、 解:等比数列{}中,公比为q,前n项和为则可以类比得出以下性质: ‎ ‎; ‎ ‎(2)若m+n=p+q,m、n、p、N ‎ 则; ‎ ‎(3)若m+n=2p,则; ‎ ‎(4)当时构成等比数列. ‎