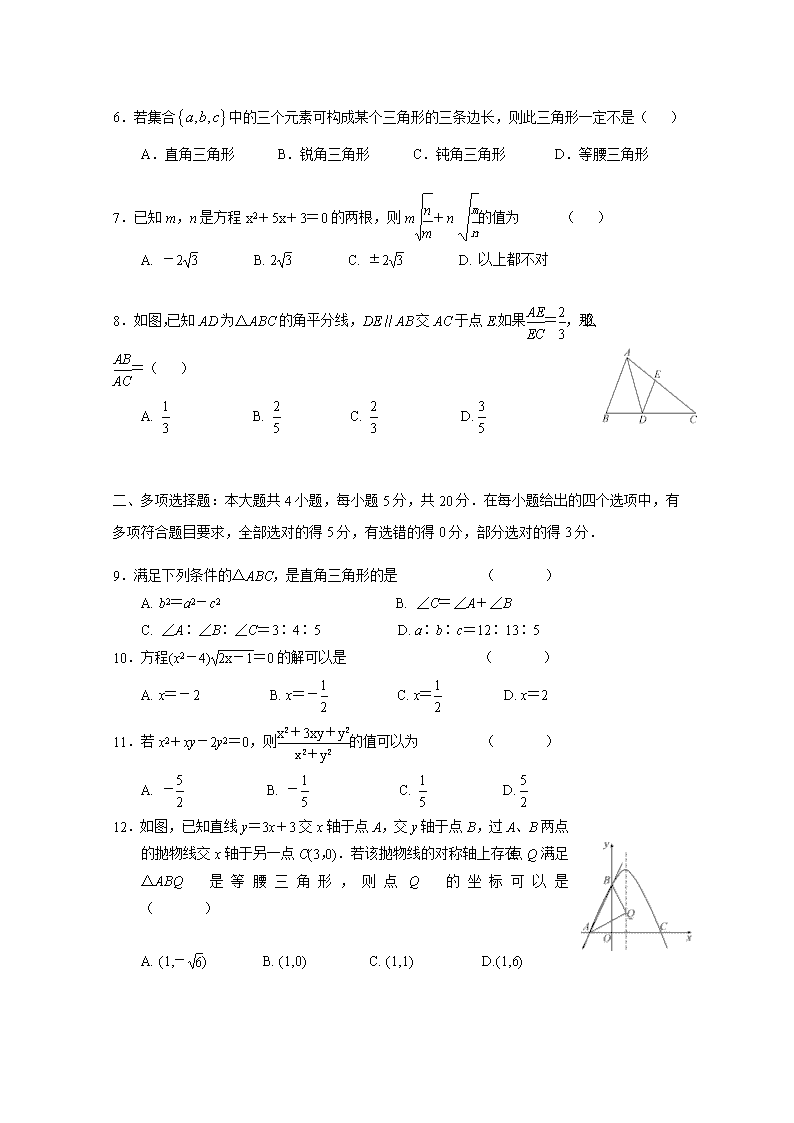江苏省启东中学2020-2021高一数学上学期期初试题（人教新课标A版附答案） 7页

江苏省启东中学2020～2021学年度第一学期期初考试 ‎ 高一数学试卷 命题人：‎ 第Ⅰ卷（选择题共60分）‎ 一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求．‎ ‎1．下列叙述正确的是 （ ）‎ A. 若|a|＝|b|，则a＝b B. 若|a|＝|b|，则a＝±b C. 若a＜b，则|a|＜|b| D. 若|a|＞|b|，则a＞b ‎2．二次根式＝－a成立的条件是 （ ）‎ A. a>0 B. a<‎0 C. a≤0 D. a是任意实数 ‎3．不论a、b为何实数，a2＋b2－‎2a－4b＋4的值 （ ）‎ A. 总是正数 B. 总是非负数 C. 可以是零 D. 可以是一切实数 ‎4．若x2－kxy＋4y2是一个完全平方式，则常数k的值为 （ ）‎ A. 4 B. －‎4 C. ±4 D. 无法确定 ‎5．一次函数y＝ax＋b(a≠0)与二次函数y＝ax2＋bx＋c在同一坐标系中的图象大致是（ ）‎ ‎6．若集合中的三个元素可构成某个三角形的三条边长，则此三角形一定不是（ ）‎ A．直角三角形 B．锐角三角形 C．钝角三角形 D．等腰三角形 ‎7．已知m，n是方程x2＋5x＋3＝0的两根，则m＋n的值为 （ ）‎ A. －2　　 B. 2　　 C. ±2　　 D. 以上都不对 ‎8．如图，已知AD为△ABC的角平分线，DE∥AB交AC于点E.如果＝，那么＝（ ）‎ A. B. C. D. 二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，有选错的得0分，部分选对的得3分．‎ ‎9．满足下列条件的△ABC，是直角三角形的是 （ ）‎ A. b2＝a2－c2 B. ∠C＝∠A＋∠B C. ∠A∶∠B∶∠C＝3∶4∶5 D. a∶b∶c＝12∶13∶5‎ ‎10．方程(x2－4)＝0的解可以是 （ ）‎ A. x＝－2 B. x＝－ C. x＝ D. x＝2‎ ‎11．若x2＋xy－2y2＝0，则的值可以为 （ ）‎ A. － B. － C. D. ‎12．如图，已知直线y＝3x＋3交x轴于点A，交y轴于点B，过A、B两点的抛物线交x轴于另一点C(3，0)．若该抛物线的对称轴上存在点Q满足△ABQ是等腰三角形，则点Q的坐标可以是 （ ）‎ A. (1,－) B. (1,0) C. (1,1) D.(1,6)‎ ‎ 第Ⅱ卷（非选择题共90分）‎ 三、填空题：本题共4小题，每小题5分，共20分．‎ ‎13．若关于x的不等式>0的解集为(－∞,－1)∪(1,＋∞)，则实数a＝________．‎ ‎14．若|x－2y－1|＋|2x－y－5|＝0，则x－y＝______．‎ ‎15．在Rt△ABC中，已知∠C＝90°，CD⊥AB，垂足为D.若AC∶BC＝3∶2，则BD∶AD的值为______．‎ ‎16．设a＝，则a是一元二次方程____________的一个实数根，据此得a4＋a2＋‎4a－3＝________．‎ 四、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（本小题满分10分）‎ 将函数的解析式变形为yx2－(y＋2)x＋y＝0，试求出函数y的最大值、最小值．‎ ‎18．（本小题满分12分）‎ 把下列各式分解因式：‎ ‎（1）a7－ab6 ；（2）(x2＋x)2－5(x2＋x)＋6 ；（3）x3＋19x－20 ．‎ ‎19．（本小题满分12分）‎ 解下列不等式：‎ ‎（1）－4＋x－x2＜0；（2）≥2；（3）|2x＋1|＋|x－2|>4．‎ ‎20．（本小题满分12分）‎ 若x1，x2是方程x2－2x－2 020＝0的两个根，试求下列各式的值：‎ ‎（1） x＋x；（2） ；（3）(x1－5)(x2－5)；（4） |x1－x2|．‎ ‎21．（本小题满分12分）‎ 已知关于x的方程x2＋2mx＋m＋2＝0．‎ ‎（1）m为何值时，方程的两个根都是正数？‎ ‎（2）m为何值时，方程的两个根一个大于0，另一个小于0，且负根的绝对值较小？‎ ‎（3）m为何值时，方程的两个根均不小于1?‎ ‎22．（本小题满分12分）‎ ‎（1）已知关于x的方程x2＋x－a－1＝0在0≤x≤1上有解，求实数a的取值范围；‎ ‎（2）已知关于x的方程x2＋x－a－1 > 0在0≤x≤1上有解，求实数a的取值范围；‎ ‎（3）已知关于x的方程x2＋x－a－1 > 0在0≤x≤1上恒成立，求实数a的取值范围．‎ 江苏省启东中学2020～2021学年度第一学期期初考试 ‎ 高一数学试卷 一、BCDCC，DAC 二、9. ABD；10. CD；11. BD；12. ABC 三、13. 1 ； 14. 2 ； 15. 4∶9 ； 16. x2＋x－1=0，0‎ 四、解答题 ‎17. 解：（1） 当y＝0时，x＝0；‎ ‎（2） 当y≠0时，‎ 关于x的一元二次方程yx2－(y＋2)x＋y＝0，‎ 由于x是实数，所以其判别式Δ≥0一定成立．‎ 由y≠0以及Δ＝(y＋2)2－4y2≥0，解得－≤y≤2且y≠0.‎ 综上所述，－≤y≤2.‎ 所以函数y的最大值、最小值分别是2和－.‎ ‎18.解：（1） a7－ab6＝a(a6－b6)＝a(a3＋b3)(a3－b3)‎ ‎＝a(a＋b)(a2－ab＋b2)(a－b)(a2＋ab＋b2)‎ ‎＝a(a＋b)(a－b)(a2＋ab＋b2)(a2－ab＋b2)‎ ‎（2）(x2＋x)2－5(x2＋x)＋6＝(x2＋x－2)(x2＋x－3)＝(x＋2)(x－1)(x＋)(x＋)；‎ ‎（3）x3＋19x－20＝(x3－1)＋19(x－1)＝(x－1)(x2＋x＋1＋19)＝(x－1)(x2＋x＋20)‎ ‎19.解：（1）整理得x2－x＋4＞0.‎ ‎∵ Δ＜0，∴ 原不等式的解集为一切实数．‎ ‎（2）4，∴ x<－1，此时x<－1；‎ 当－4，∴ x>1，此时14，∴ x>，此时x≥2.‎ 综上可得，原不等式的解集为x<－1或x>1.‎ ‎20.解：由题意，根据根与系数的关系，得x1＋x2＝2，x1x2＝－2 020.‎ ‎（1）x＋x＝(x1＋x2)2－2x1x2＝22－2×(－2 020)＝4 044.‎ ‎（2） ＋＝＝＝－.‎ ‎（3）(x1－5)(x2－5)＝x1x2－5(x1＋x2)＋25＝－2 020－5×2＋25＝－2 005.‎ ‎（4） |x1－x2|＝＝＝＝2.‎ ‎21.解：(1) ⇒－2＜m≤－1.‎ ‎(2) ⇒m＜－2.‎ ‎(3) ⇒m=－1.‎ ‎22．解：（1）将方程变形为a＝x2＋x－1，要求a的取值范围，就是求y＝x2＋x－1的取值范围，即y＝(x＋)2－，0≤x≤1，‎ 所以当x＝0时，y取得最小值为－1；当x＝1时，y取得最大值为1，‎ 所以y的取值范围是－1≤y≤1，‎ 即实数a的取值范围是－1≤a≤1.‎ ‎（2）由（1）知a < 1．‎ ‎（3）由（1）知a < －1． ‎