数学卷·2018届辽宁省盘锦市辽河油田二中高二上学期10月月考数学试卷（解析版） 15页

全*品*高*考*网， 用后离不了！2016-2017学年辽宁省盘锦市辽河油田二中高二（上）10月月考数学试卷 ‎　‎ 一、选择题（每道小题5分，满分60分）‎ ‎1．命题“∀x＞0，x2﹣x≤0”的否定是（　　）‎ A．∃x0＞0，x02﹣x0≤0 B．∃x0＞0，x02﹣x0＞0‎ C．∀x＞0，x2﹣x＞0 D．∀x≤0，x2﹣x＞0‎ ‎2．抛物线y=2x2的准线方程为（　　）‎ A． B． C． D．‎ ‎3．某单位有老年人27人，中年人54人，青年人81人，为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为42的样本，则老年人、中年人、青年人分别应抽取的人数是（　　）‎ A．7，11，18 B．6、12、18 C．6、13、17 D．7、14、21‎ ‎4．在区间[0，3]上随机地取一个实数x，则事件“1≤2x﹣1≤3”发生的概率为（　　）‎ A． B． C． D．‎ ‎5．命题“若xy=0，则x2+y2=0”与它的逆命题、否命题、逆否命题中，真命题的个数为（　　）‎ A．0 B．1 C．2 D．4‎ ‎6．一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4，从袋中随机取出两个球，则取出的球的编号之和不大于4的概率是（　　）‎ A． B． C． D．‎ ‎7．在班级的演讲比赛中，将甲、乙两名同学的得分情况制成如图所示的茎叶图．记甲、乙两名同学所得分数的平均分分别为甲、乙，则下列判断正确的是（　　）‎ A．甲＜乙，甲比乙成绩稳定 B．甲＞乙，甲比乙成绩稳定 C．甲＜乙，乙比甲成绩稳定 D．甲＞乙，乙比甲成绩稳定 ‎8．如图所示，程序框图（算法流程图）的输出结果是（　　）‎ A． B． C． D．‎ ‎9．下列命题错误的是（　　）‎ A．命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2≠0”‎ B．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件 C．若p∧q为假命题，则p、q均为假命题 D．对于命题p：∃x∈R，x2+x+1＜0，则￢p：∀x∈R，x2+x+1≥0‎ ‎10．已知a＞b＞0，椭圆C1的方程为+=1，双曲线C2的方程为﹣=1，C1与C2的离心率之积为，则C2的渐近线方程为（　　）‎ A．x±2y=0 B．2x±y=0 C．x±4y=0 D．4x±y=0‎ ‎11．设F1，F2分别为双曲线﹣=1（a＞0，b＞0）的左、右焦点，若在双曲线的右支上存在点P，满足|PF2|=|F1F2|，且原点O到直线PF1的距离等于双曲线的实轴长，则该双曲线的渐近线方程为（　　）‎ A．4x±3y=0 B．3x±5y=0 C．3x±4y=0 D．5x±3y=0‎ ‎12．已知抛物线y2=2px的焦点F与双曲线的右焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上且|AK|=|AF|，则△AFK的面积为（　　）‎ A．4 B．8 C．16 D．32‎ ‎　‎ 二、填空题（每道小题5分，满分20）‎ ‎13．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组一次为[20，40），[40，60），[60，80），[80，100），若低于60分的人数是15人，则该班的学生人数是　　．‎ ‎14．甲、乙两人随意住两间空房，则甲、乙两人各住一间房的概率是　　．‎ ‎15．椭圆+=1的焦距为2，则m的值等于　　．‎ ‎16．若椭圆过抛物线y2=8x的焦点，且与双曲线x2﹣y2=1有相同的焦点，则该椭圆的方程为　　．‎ ‎　‎ 三、简答题（满分70分）‎ ‎17．求适合下列条件的椭圆的标准方程：‎ ‎（1）焦点在y轴上，焦距是4，且经过点M（3，2）；‎ ‎（2）焦距是10，且椭圆上一点到两焦点的距离的和为26．‎ ‎18．盒中有3个白球，2个红球，从中任取2个球．求：‎ ‎（1）取到的两球都是红球的概率．‎ ‎（2）取到一个白球，一个红球的概率．‎ ‎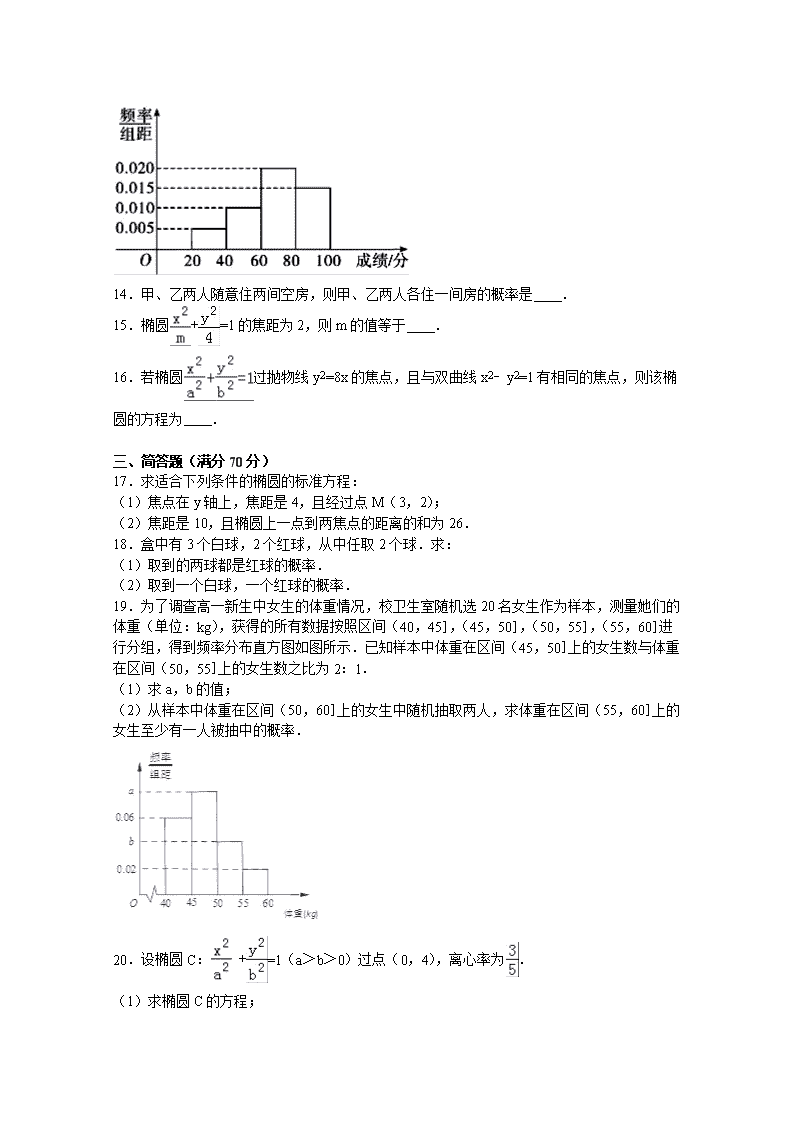19．为了调查高一新生中女生的体重情况，校卫生室随机选20名女生作为样本，测量她们的体重（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]进行分组，得到频率分布直方图如图所示．已知样本中体重在区间（45，50]上的女生数与体重在区间（50，55]上的女生数之比为2：1．‎ ‎（1）求a，b的值；‎ ‎（2）从样本中体重在区间（50，60]上的女生中随机抽取两人，求体重在区间（55，60]上的女生至少有一人被抽中的概率．‎ ‎20．设椭圆C： +=1（a＞b＞0）过点（0，4），离心率为．‎ ‎（1）求椭圆C的方程；‎ ‎（2）求过点（3，0）且斜率为的直线被椭圆所截得线段的中点坐标．‎ ‎21．某车间为了规定工时定额，需要确定加个某零件所花费的时间，为此作了四次实验，得到的数据如下：‎ 零件的个数x（个）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 加工的时间y（小时）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ ‎（1）求出y关于x的线性回归方程；‎ ‎（2）试预测加工10个零件需要多少时间？‎ ‎22．已知：命题p：方程表示焦点在y轴上的椭圆．命题q：双曲线的离心率e∈（2，3）．若p∨q为真，p∧q为假，求实数m的取值范围．‎ ‎　‎ ‎2016-2017学年辽宁省盘锦市辽河油田二中高二（上）10月月考数学试卷 参考答案与试题解析 ‎　‎ 一、选择题（每道小题5分，满分60分）‎ ‎1．命题“∀x＞0，x2﹣x≤0”的否定是（　　）‎ A．∃x0＞0，x02﹣x0≤0 B．∃x0＞0，x02﹣x0＞0‎ C．∀x＞0，x2﹣x＞0 D．∀x≤0，x2﹣x＞0‎ ‎【考点】命题的否定．‎ ‎【分析】根据全称命题的否定是特称命题即可得到结论．‎ ‎【解答】解：命题是全称命题，‎ 则命题“∀x＞0，x2﹣x≤0”的否定是：‎ ‎∃x0＞0，x02﹣x0＞0，‎ 故选：B ‎　‎ ‎2．抛物线y=2x2的准线方程为（　　）‎ A． B． C． D．‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】先把抛物线化为标准方程为x2=y，再求准线．‎ ‎【解答】解：∵抛物线的标准方程为x2=y，‎ ‎∴p=，开口朝上，‎ ‎∴准线方程为y=﹣，‎ 故选D．‎ ‎　‎ ‎3．某单位有老年人27人，中年人54人，青年人81人，为了调查他们的身体状况的某项指标，需从他们中间抽取一个容量为42的样本，则老年人、中年人、青年人分别应抽取的人数是（　　）‎ A．7，11，18 B．6、12、18 C．6、13、17 D．7、14、21‎ ‎【考点】分层抽样方法．‎ ‎【分析】由题意，要计算各层中所抽取的人数，根据分层抽样的规则，求出各层应抽取的人数即可选出正确选项．‎ ‎【解答】解：由题意，老年人、中年人、青年人比例为1：2：3．‎ 由分层抽样的规则知，老年人应抽取的人数为×42=7人，‎ 中年人应抽取的人数为×42=14人，‎ 青年人应抽取的人数为×42=21人．‎ 故选：D．‎ ‎　‎ ‎4．在区间[0，3]上随机地取一个实数x，则事件“1≤2x﹣1≤3”发生的概率为（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】首先求出事件“1≤2x﹣1≤3”发生对应的区间长度，利用几何概型公式解答．‎ ‎【解答】解：在区间[0，3]上随机地取一个实数x，则事件“1≤2x﹣1≤3”发生，即1≤x≤2，区间长度为1，‎ 由几何概型公式得到事件“1≤2x﹣1≤3”发生的概率为；‎ 故选：B．‎ ‎　‎ ‎5．命题“若xy=0，则x2+y2=0”与它的逆命题、否命题、逆否命题中，真命题的个数为（　　）‎ A．0 B．1 C．2 D．4‎ ‎【考点】四种命题的真假关系；四种命题．‎ ‎【分析】先写出其命题的逆命题，只要判断原命题和其逆命题的真假即可，根据互为逆否命题的两个命题真假相同，即可判定其否命题、逆否命题的真假．‎ ‎【解答】解：“若xy=0，则x2+y2=0”，是假命题，‎ 其逆命题为：“若x2+y2=0，则xy=0”是真命题，‎ 据互为逆否命题的两个命题真假相同，可知其否命题为真命题、逆否命题是假命题，‎ 故真命题的个数为2‎ 故选C．‎ ‎　‎ ‎6．一个袋中装有四个形状大小完全相同的球，球的编号分别为1，2，3，4，从袋中随机取出两个球，则取出的球的编号之和不大于4的概率是（　　）‎ A． B． C． D．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【分析】所有的取法共有C42种，用列举法求得取出的球的编号之和不大于4的取法有2种，由此求得取出的球的编号之和不大于4的概率 ‎【解答】解：∵所有的取法共有C42=6种，‎ 取出的球的编号之和不大于4的取法有（1，2）、（1，3）共2种，‎ ‎∴取出的球的编号之和不大于4的概率为=，‎ 故选B．‎ ‎　‎ ‎7．在班级的演讲比赛中，将甲、乙两名同学的得分情况制成如图所示的茎叶图．记甲、乙两名同学所得分数的平均分分别为甲、乙，则下列判断正确的是（　　）‎ A．甲＜乙，甲比乙成绩稳定 B．甲＞乙，甲比乙成绩稳定 C．甲＜乙，乙比甲成绩稳定 D．甲＞乙，乙比甲成绩稳定 ‎【考点】众数、中位数、平均数．‎ ‎【分析】由茎叶图知分别求出两组数据的平均数和方差，由此能求出结果．‎ ‎【解答】解：由茎叶图知：‎ ‎=（76+77+88+90+94）=85，‎ ‎= [（76﹣85）2+（77﹣85）2+（88﹣85）2+（90﹣85）2+（94﹣85）2]=52，‎ ‎=（75+86+88+88+93）=86，‎ ‎= [（75﹣86）2+（86﹣86）2+（88﹣86）2+（88﹣86）2+（93﹣86）2]=35.6，‎ ‎∴甲＜乙，乙比甲成绩稳定．‎ 故选：C．‎ ‎　‎ ‎8．如图所示，程序框图（算法流程图）的输出结果是（　　）‎ A． B． C． D．‎ ‎【考点】程序框图．‎ ‎【分析】分析程序中各变量、各语句的作用，分析可知：该程序的作用是计算并输出S=++的值，并输出．‎ ‎【解答】解：分析程序中各变量、各语句的作用，‎ 再根据流程图所示的顺序，可知：‎ 该程序的作用是计算并输出S=++的值 ‎∵S=++=．‎ 故选D．‎ ‎　‎ ‎9．下列命题错误的是（　　）‎ A．命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2≠0”‎ B．“x＞2”是“x2﹣3x+2＞0”的充分不必要条件 C．若p∧q为假命题，则p、q均为假命题 D．对于命题p：∃x∈R，x2+x+1＜0，则￢p：∀x∈R，x2+x+1≥0‎ ‎【考点】复合命题的真假．‎ ‎【分析】A．逆否命题 条件结论都否定后位置互换 B，x＞2可推出x2﹣3x+2＞0成立，但x2﹣3x+2＞0等价于x＞2或x＜1‎ 通过分析可得A，B，D均正确．‎ ‎【解答】解：∵若p则q的逆否命题是若非q，则非p，∴命题“若x2﹣3x+2=0，则x=1”的逆否命题为“若x≠1，则x2﹣3x+2≠0”是真命题 ‎∵x2﹣3x+2＞0⇔x＞2或x＜1，∴x＞2⇒x2﹣3x+2＞0∴B是真命题 ‎∵全称命题的否定特称命题，对于命题p：∃x∈R，x2+x+1＜0，则¬p：∀x∈R，x2+x+1≥0，∴C是真命题．‎ ‎∵p∧q一假即为假，∴C答案错误．‎ 故选C ‎　‎ ‎10．已知a＞b＞0，椭圆C1的方程为+=1，双曲线C2的方程为﹣=1，C1与C2的离心率之积为，则C2的渐近线方程为（　　）‎ A．x±2y=0 B．2x±y=0 C．x±4y=0 D．4x±y=0‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】运用椭圆和双曲线的离心率公式，由离心率之积，求得a=2b，再由渐近线方程即可得到．‎ ‎【解答】解：设椭圆C1： +=1的离心率为e1，则e1=，‎ 设双曲线C2：﹣=1的离心率为e2，则e2=，‎ 由C1与C2的离心率之积为，‎ 即有e1e2=，‎ 即=，‎ 化简可得=，‎ 则C2的渐近线方程为y=±x，‎ 即为y=±x．‎ 故选：A．‎ ‎　‎ ‎11．设F1，F2分别为双曲线﹣=1（a＞0，b＞0）的左、右焦点，若在双曲线的右支上存在点P，满足|PF2|=|F1F2|，且原点O到直线PF1的距离等于双曲线的实轴长，则该双曲线的渐近线方程为（　　）‎ A．4x±3y=0 B．3x±5y=0 C．3x±4y=0 D．5x±3y=0‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】利用题设条件和双曲线性质在三角形中寻找等量关系，得出a与b之间的等量关系，进而求出双曲线的渐近线方程．‎ ‎【解答】解：依题意|PF2|=|F1F2|，可知三角形PF2F1是一个等腰三角形，F2在直线PF1的投影是其中点，‎ 由勾股定理可知|PF1|=4b 根据双曲定义可知4b﹣2c=2a，整理得c=2b﹣a，‎ 代入c2=a2+b2整理得3b2﹣4ab=0，求得=，‎ ‎∴双曲线的渐近线方程为y=±x，即4x±3y=0．‎ 故选：A．‎ ‎　‎ ‎12．已知抛物线y2=2px的焦点F与双曲线的右焦点重合，抛物线的准线与x轴的交点为K，点A在抛物线上且|AK|=|AF|，则△AFK的面积为（　　）‎ A．4 B．8 C．16 D．32‎ ‎【考点】抛物线的简单性质；双曲线的简单性质．‎ ‎【分析】由双曲线得右焦点为（4，0）即为抛物线y2=2px的焦点，可得p．进而得到抛物线的方程和其准线方程，可得K坐标．过点A作AM⊥准线，垂足为点M．则|AM|=|AF|．可得|AK|=|AM|．可得|KF|=|AF|．进而得到面积．‎ ‎【解答】解：由双曲线得右焦点为（4，0）即为抛物线y2=2px的焦点，∴，解得p=8．‎ ‎∴抛物线的方程为y2=16x．‎ 其准线方程为x=﹣4，∴K（﹣4，0）．‎ 过点A作AM⊥准线，垂足为点M．则|AM|=|AF|．‎ ‎∴|AK|=|AM|．‎ ‎∴∠MAK=45°．‎ ‎∴|KF|=|AF|．‎ ‎∴=32．‎ 故选D．‎ ‎　‎ 二、填空题（每道小题5分，满分20）‎ ‎13．某学校组织学生参加英语测试，成绩的频率分布直方图如图，数据的分组一次为[20，40），[40，60），[60，80），[80，100），若低于60分的人数是15人，则该班的学生人数是　50　．‎ ‎【考点】频率分布直方图．‎ ‎【分析】由已知中的频率分布直方图，我们可以求出成绩低于60分的频率，结合已知中的低于60分的人数是15人，结合频数=频率×总体容量，即可得到总体容量．‎ ‎【解答】解：∵成绩低于60分有第一、二组数据，‎ 在频率分布直方图中，对应矩形的高分别为0.005，0.01，‎ 每组数据的组距为20‎ 则成绩低于60分的频率P=（0.005+0.010）×20=0.3，‎ 又∵低于60分的人数是15人，‎ 则该班的学生人数是=50．‎ 故答案为：50‎ ‎　‎ ‎14．甲、乙两人随意住两间空房，则甲、乙两人各住一间房的概率是　0.5　．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【分析】甲，乙两人随意入住两间空房，每人有两种住法，故两人有2×2=4种住法，且每种住法出现的可能性相等，故为古典概型．只要再计算出甲乙两人各住一间房的住法种数A22=2，求比值即可．‎ ‎【解答】解：由题意符合古典概型，甲，乙两人随意入住两间空房，每人有两种住法，故两人有2×2=4种住法，甲乙两人各住一间房的住法种数A22=2，所以甲、乙两人各住一间房的概率为P==0.5，‎ 故答案为：0.5．‎ ‎　‎ ‎15．椭圆+=1的焦距为2，则m的值等于　3或5　．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】由题意可得：c=1，再分别讨论焦点的位置进而求出m的值．‎ ‎【解答】解：由题意可得：c=1．‎ ‎①当椭圆的焦点在x轴上时，m﹣4=1，解得m=5．‎ ‎②当椭圆的焦点在y轴上时，4﹣m=1，解得m=3．‎ 故答案为：3或5．‎ ‎　‎ ‎16．若椭圆过抛物线y2=8x的焦点，且与双曲线x2﹣y2=1有相同的焦点，则该椭圆的方程为　　．‎ ‎【考点】椭圆的标准方程．‎ ‎【分析】求得抛物线、双曲线的焦点坐标，从而可得椭圆的几何量，由此可得结论．‎ ‎【解答】解：抛物线y2=8x的焦点坐标为（2，0），双曲线x2﹣y2=1的焦点坐标为（，0）‎ 由题意，，∴a2=4，b2=2‎ ‎∴椭圆的方程为 故答案为：‎ ‎　‎ 三、简答题（满分70分）‎ ‎17．求适合下列条件的椭圆的标准方程：‎ ‎（1）焦点在y轴上，焦距是4，且经过点M（3，2）；‎ ‎（2）焦距是10，且椭圆上一点到两焦点的距离的和为26．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由题意可设椭圆的方程为，联立，解出即可．．‎ ‎（2）由题意可得，解出即可．‎ ‎【解答】解：（1）由题意可设椭圆的方程为，‎ 联立，解得．‎ ‎∴椭圆的标准方程是．‎ ‎（2）由题意可得，解得．‎ 故所求的椭圆方程为或．‎ ‎　‎ ‎18．盒中有3个白球，2个红球，从中任取2个球．求：‎ ‎（1）取到的两球都是红球的概率．‎ ‎（2）取到一个白球，一个红球的概率．‎ ‎【考点】列举法计算基本事件数及事件发生的概率．‎ ‎【分析】利用列举法确定基本事件的个数，即可得出结论．‎ ‎【解答】解：将3个白球编号为1，2，3；两个红球编号为4，5．从中任取2个球，包含以下基本事件：（1，2），（1，3），（1，4），（1，5），（2，3），（2，4），（2，5），（3，4），（3，5），（4，5）．‎ 共计10种情况…‎ ‎（1）：记事件A表示“取到的两个球都是红球”，那么事件A只有（4，5）一种结果．‎ 所以，…‎ ‎（2）：记事件B表示“取到一个白球，一个红球”，那么事件B包含：（1，4），（1，5），（2，4），（2，5），（3，4），（3，5）共计6种可能结果．…‎ 所以，P（B）==…‎ ‎　‎ ‎19．为了调查高一新生中女生的体重情况，校卫生室随机选20名女生作为样本，测量她们的体重（单位：kg），获得的所有数据按照区间（40，45]，（45，50]，（50，55]，（55，60]进行分组，得到频率分布直方图如图所示．已知样本中体重在区间（45，50]上的女生数与体重在区间（50，55]上的女生数之比为2：1．‎ ‎（1）求a，b的值；‎ ‎（2）从样本中体重在区间（50，60]上的女生中随机抽取两人，求体重在区间（55，60]上的女生至少有一人被抽中的概率．‎ ‎【考点】列举法计算基本事件数及事件发生的概率．‎ ‎【分析】（1）根据频率的求法及所有小组的频率和为1，构造关于a，b的方程组，解之即得a，b的值；‎ ‎（2）根据概率的求法，计算可得答案，分别求出包含基本事件及从（50，60]中任意抽取2个个体基本事件总数，最后求出它们的比值即可．‎ ‎【解答】解：（1）样本中体重在区间（45，50]上的女生有a×5×20=100a（人），‎ 样本中体重在区间（50，55]上的女生有b×5×20=100b（人），‎ 依题意，有100a=2×100b，即a=2b①，﹣﹣﹣﹣﹣﹣﹣﹣‎ 根据频率分布直方图可知（0.02+b+0.06+a）×5②，﹣﹣﹣﹣﹣﹣﹣﹣‎ 联立①②得：a=0.08，b=0.04；﹣﹣﹣﹣﹣﹣﹣﹣‎ ‎（2）样本中体重在区间（50，55]上的女生有0.04×5×20=4人，‎ 体重在区间（55，60]上的女生有0.2×5×20=2人，‎ 可知从这6名女生中随机抽取两人共有15种情况，‎ 可知其中体重在（55，60]上的女生至少有一人共有9种情况，‎ 记“从样本中体重在区间（50，60]上的女生随机抽取两人，‎ 体重在区间（55，60]上的女生至少有一人被抽中”为事件M，‎ 则．﹣﹣﹣﹣﹣﹣﹣‎ ‎　‎ ‎20．设椭圆C： +=1（a＞b＞0）过点（0，4），离心率为．‎ ‎（1）求椭圆C的方程；‎ ‎（2）求过点（3，0）且斜率为的直线被椭圆所截得线段的中点坐标．‎ ‎【考点】直线与圆锥曲线的综合问题．‎ ‎【分析】（1）椭圆C： +=1（a＞b＞0）过点（0，4），可求b，利用离心率为，求出a，即可得到椭圆C的方程；‎ ‎（2）过点（3，0）且斜率为的直线为y=（x﹣3），代入椭圆C方程，整理，利用韦达定理，确定线段的中点坐标．‎ ‎【解答】解：（1）将点（0，4）代入椭圆C的方程得=1，∴b=4，…‎ 由e==，得1﹣=，∴a=5，…‎ ‎∴椭圆C的方程为+=1．…‎ ‎（2）过点（3，0）且斜率为的直线为y=（x﹣3），…‎ 设直线与椭圆C的交点为A（x1，y1），B（x2，y2），‎ 将直线方程y=（x﹣3）代入椭圆C方程，整理得x2﹣3x﹣8=0，…‎ 由韦达定理得x1+x2=3，‎ y1+y2=（x1﹣3）+（x2﹣3）=（x1+x2）﹣=﹣．…‎ 由中点坐标公式AB中点横坐标为，纵坐标为﹣，‎ ‎∴所截线段的中点坐标为（，﹣）．…‎ ‎　‎ ‎21．某车间为了规定工时定额，需要确定加个某零件所花费的时间，为此作了四次实验，得到的数据如下：‎ 零件的个数x（个）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 加工的时间y（小时）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ ‎（1）求出y关于x的线性回归方程；‎ ‎（2）试预测加工10个零件需要多少时间？‎ ‎【考点】回归分析的初步应用．‎ ‎【分析】（1）根据表中所给的数据，做出横标和纵标的平均数，得到样本中心点，求出对应的横标和纵标的积的和，求出横标的平方和，做出系数和a的值，写出线性回归方程．‎ ‎（2）将x=10代入回归直线方程，得y=0.7×10+1.05=8.05．试预测加工10个零件需要8.05个小时，这是一个预报值．‎ ‎【解答】解：（1）由表中数据得： xiyi=52.5， =3.5， =3.5， xi2=54．‎ ‎∴b==0.7‎ 故a=3.5﹣0.7×3.5=1.05，‎ ‎∴所求线性回归方程为：y=0.7x+1.05．‎ ‎（2）将x=10代入回归直线方程，得y=0.7×10+1.05=8.05（小时）．‎ ‎∴试预测加工10个零件需要8.05个小时．‎ ‎　‎ ‎22．已知：命题p：方程表示焦点在y轴上的椭圆．命题q：双曲线的离心率e∈（2，3）．若p∨q为真，p∧q为假，求实数m的取值范围．‎ ‎【考点】命题的真假判断与应用；椭圆的定义；双曲线的简单性质．‎ ‎【分析】根据题意求出命题p、q为真时m的范围分别为0＜m＜5、．由p∨q为真，p∧q为假得p真q假，或p假q真，进而求出答案即可．‎ ‎【解答】解：若p为真，则，得到0＜m＜5； ‎ 若q为真，则，即4a2＜a2+b2＜9a2，得到3a2＜b2＜8a2，于是6＜3m＜16，可得，． ‎ 由由题p∨q为真，p∧q为假，可知p真q假，或p假q真． ‎ p真q假时，，得到0＜m≤2； ‎ p假q真时，，得到； ‎ 综上所述，实数m的取值范围为．‎ ‎　‎