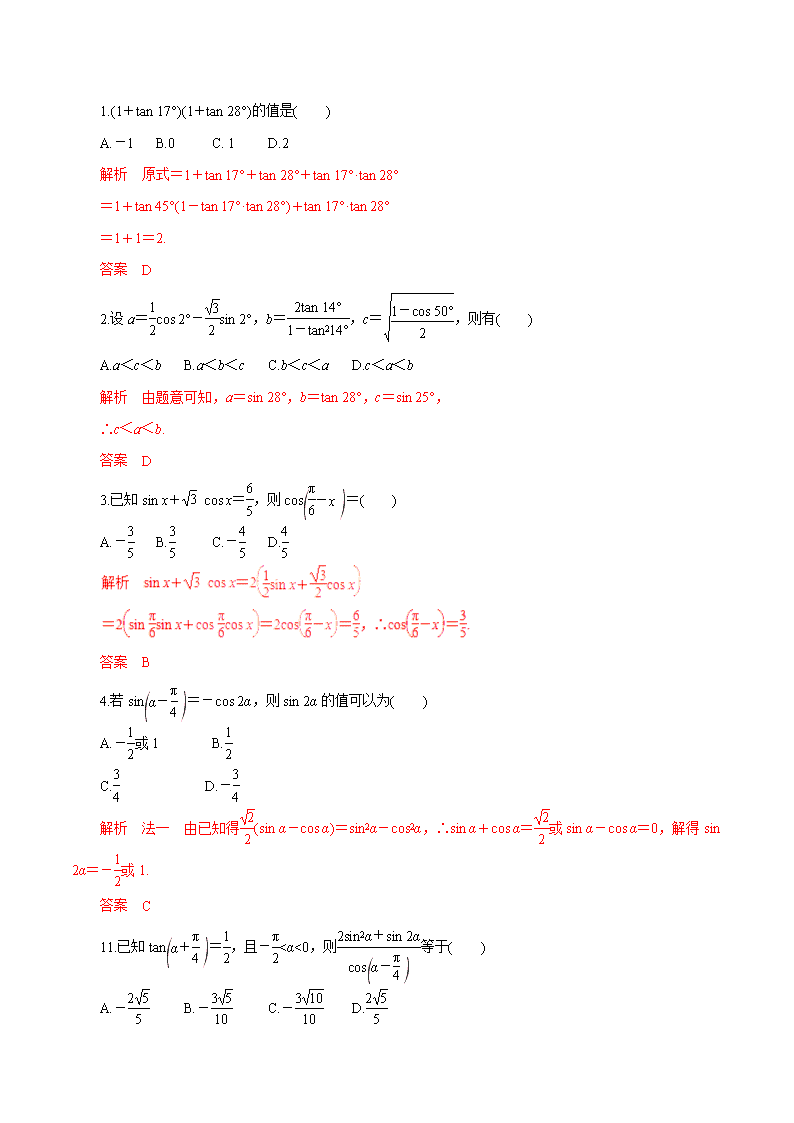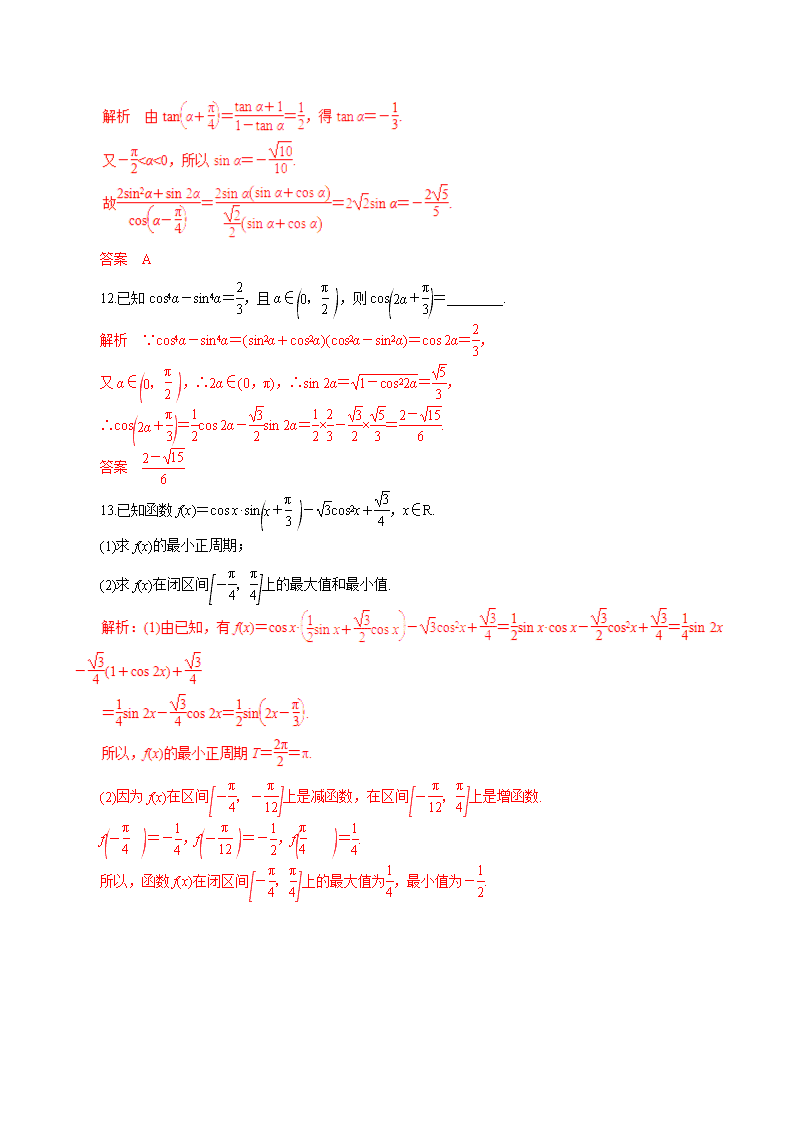专题14+两角和与差的三角函数（题型专练）-2019年高考数学（文）热点题型和提分秘籍 2页

‎1.(1＋tan 17°)(1＋tan 28°)的值是(　　)‎ A.－1 B.0 C. 1 D.2‎ 解析　原式＝1＋tan 17°＋tan 28°＋tan 17°·tan 28°‎ ‎＝1＋tan 45°(1－tan 17°·tan 28°)＋tan 17°·tan 28°‎ ‎＝1＋1＝2.‎ 答案　D ‎2.设a＝cos 2°－sin 2°，b＝，c＝，则有(　　)‎ A.a＜c＜b B.a＜b＜c C.b＜c＜a D.c＜a＜b 解析　由题意可知，a＝sin 28°，b＝tan 28°，c＝sin 25°，‎ ‎∴c＜a＜b.‎ 答案　D ‎3.已知sin x＋ cos x＝，则cos＝(　　)‎ A.－ B. C.－ D. 答案　B ‎4.若sin＝－cos 2α，则sin 2α的值可以为(　　)‎ A.－或1 B. C. D.－ 解析　法一　由已知得(sin α－cos α)＝sin2α－cos2α，∴sin α＋cos α＝或sin α－cos α＝0，解得sin 2α＝－或1. ‎ 答案　C ‎11.已知tan＝，且－<α<0，则等于(　　)‎ A.－ B.－ C.－ D. 答案　A ‎12.已知cos4α－sin4α＝，且α∈，则cos＝________.‎ 解析　∵cos4α－sin4α＝(sin2α＋cos2α)(cos2α－sin2α)＝cos 2α＝，‎ 又α∈，∴2α∈(0，π)，∴sin 2α＝＝，‎ ‎∴cos＝cos 2α－sin 2α＝×－×＝.‎ 答案　 ‎13.已知函数f(x)＝cos x·sin－cos2x＋，x∈R.‎ ‎(1)求f(x)的最小正周期；‎ ‎(2)求f(x)在闭区间上的最大值和最小值.‎ ‎(2)因为f(x)在区间上是减函数，在区间上是增函数.‎ f＝－，f＝－，f＝.‎ 所以，函数f(x)在闭区间上的最大值为，最小值为－. ‎