数学卷·2018届广东省韶关市仁化一中高二上学期月考数学试卷（文科）（3）（解析版） 16页

‎2016-2017学年广东省韶关市仁化一中高二（上）月考数学试卷（文科）（3）‎ ‎　‎ 一、选择题：本大题共10小题，每个小题目只有一个正确选择项，每小题5分，满分50分．‎ ‎1．设全集U={1，2，3，4，5，6}，A={4，5}，B={3，4}，则∁U（A∪B）=（　　）‎ A．{3，4，5} B．{1，2，3，4，6} C．{1，2，6} D．{1，2，3，5，6}‎ ‎2．已知向量=（1，﹣2），=（x，2），若⊥，则=（　　）‎ A． B． C．5 D．20‎ ‎3．若等差数列{an}的前5项和S5=25，且a2=3，则a7=（　　）‎ A．12 B．13 C．14 D．15‎ ‎4．已知a，b都是实数，那么“a2＞b2”是“a＞b”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎5．已知椭圆+=1上一点P到椭圆的一个焦点的距离为3，则点P到另一个焦点的距离为（　　）‎ A．2 B．3 C．5 D．7‎ ‎6．已知命题p：∃x∈R，x2﹣3x+3≤0，则（　　）‎ A．￢p：∃x∈R，x2﹣3x+3＞0，且￢p为真命题 B．￢p：∃x∈R，x2﹣3x+3＞0，且￢p为假命题 C．￢p：∀x∈R，x2﹣3x+3＞0，且￢p为真命题 D．￢p：∀x∈R，x2﹣3x+3＞0，且￢p为假命题 ‎7．在△ABC中，若∠A=60°，∠B=45°，BC=3，则AC=（　　）‎ A． B． C． D．‎ ‎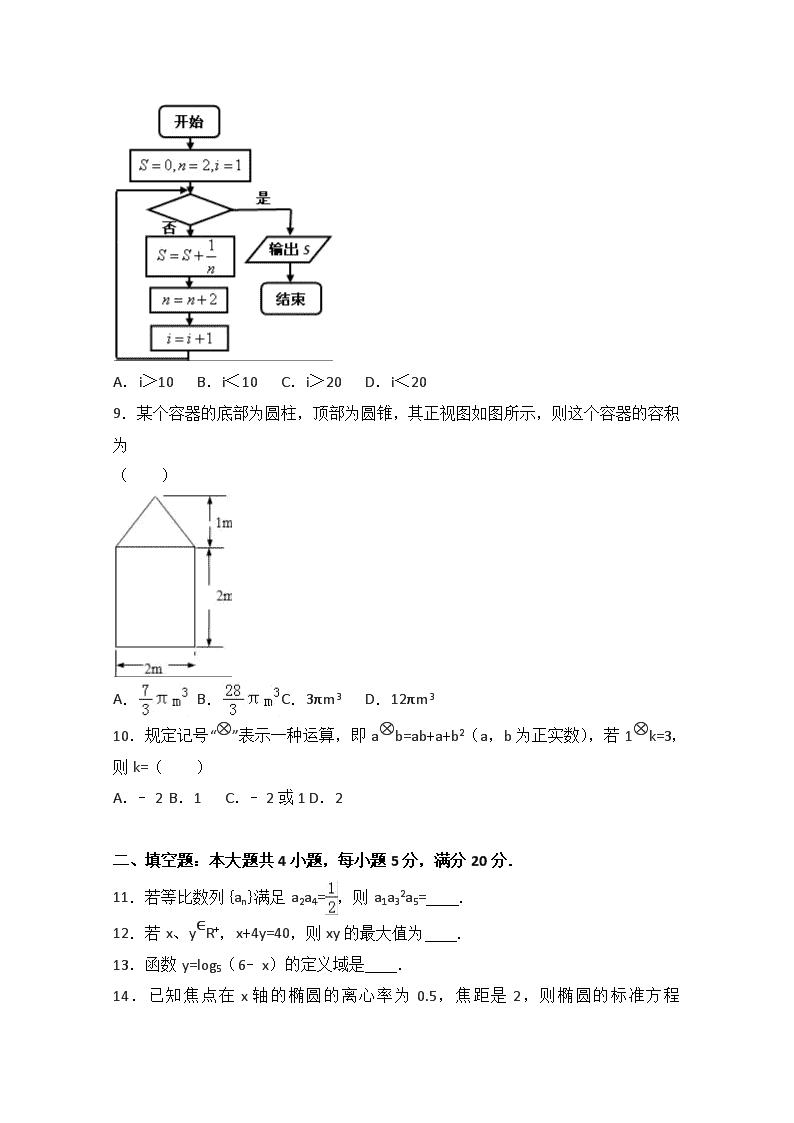8．给出计算的值的一个程序框图如图，其中判断框内应填入的条件是（　　）‎ A．i＞10 B．i＜10 C．i＞20 D．i＜20‎ ‎9．某个容器的底部为圆柱，顶部为圆锥，其正视图如图所示，则这个容器的容积为 ‎（　　）‎ A． B． C．3πm3 D．12πm3‎ ‎10．规定记号“⊗”表示一种运算，即a⊗b=ab+a+b2（a，b为正实数），若1⊗k=3，则k=（　　）‎ A．﹣2 B．1 C．﹣2或1 D．2‎ ‎　‎ 二、填空题：本大题共4小题，每小题5分，满分20分．‎ ‎11．若等比数列{an}满足a2a4=，则a1a32a5=　　．‎ ‎12．若x、y∈R+，x+4y=40，则xy的最大值为　　．‎ ‎13．函数y=log5（6﹣x）的定义域是　　．‎ ‎14．已知焦点在x轴的椭圆的离心率为0.5，焦距是2，则椭圆的标准方程是　　．‎ ‎　‎ 三、解答题：本大题共6小题，满分80分．（解答须写出文字说明、证明过程和演算步骤）．‎ ‎15．已知函数f（x）=sinx+cosx，x∈R ‎（Ⅰ）求f（x）的最小正周期；‎ ‎（Ⅱ） 若f（α）=，求sin2α的值．‎ ‎16．一个口袋中装有大小相同的2个白球和3个黑球．‎ ‎（1）采取不放回抽样方式，从中摸出两个球，写出所有的基本事件；‎ ‎（2）采取放回抽样方式，从中摸出两个球，求两球恰好颜色不同的概率．‎ ‎17．设x，y满足约束条件则z=2x+y的最大值为　　．‎ ‎18．在长方体ABCD﹣A1B1C1D1中，已知AB=BC=2，BB1=3，连接BC1，过B1作B1E⊥BC1交CC1于点E．‎ ‎（1）求证：B1E⊥平面ABC1；‎ ‎（2）求三棱锥C1﹣B1D1E的体积．‎ ‎19．若数列{an}的前n项和Sn=n2﹣10n（n=1，2，3，…），‎ ‎（1）求a1，a2的值；‎ ‎（2）求此数列的通项公式．‎ ‎20．在平面直角坐标系xoy中，已知椭圆C1： =1（a＞b＞0）的左焦点F1（﹣5，0），且点P（0，12）在C1上．‎ ‎（1）求C1的方程；‎ ‎（2）若点M到椭圆C1的左焦点与右焦点的距离之比为2：3，求点M的坐标（x，y）满足的方程．‎ ‎　‎ ‎2016-2017学年广东省韶关市仁化一中高二（上）月考数学试卷（文科）（3）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每个小题目只有一个正确选择项，每小题5分，满分50分．‎ ‎1．设全集U={1，2，3，4，5，6}，A={4，5}，B={3，4}，则∁U（A∪B）=（　　）‎ A．{3，4，5} B．{1，2，3，4，6} C．{1，2，6} D．{1，2，3，5，6}‎ ‎【考点】交、并、补集的混合运算．‎ ‎【分析】先由集合A，B求出A∪B，在求出∁U（A∪B）即可以得到正确答案．‎ ‎【解答】解：∵A={4，5}，B={3，4}，‎ ‎∴A∪B={3，4，5}，‎ 又∵U={1，2，3，4，5，6}，‎ ‎∴∁U（A∪B）={1，2，6}．‎ 故选C ‎　‎ ‎2．已知向量=（1，﹣2），=（x，2），若⊥，则=（　　）‎ A． B． C．5 D．20‎ ‎【考点】平面向量数量积的坐标表示、模、夹角．‎ ‎【分析】由题意可得 =0，求得x的值，可得的坐标，根据向量的模的定义求出．‎ ‎【解答】解：由题意可得 =（1，﹣2）•（x，2）=x﹣4=0，解得x=4．‎ 故==2，‎ 故选B．‎ ‎　‎ ‎3．若等差数列{an}的前5项和S5=25，且a2=3，则a7=（　　）‎ A．12 B．13 C．14 D．15‎ ‎【考点】等差数列的前n项和；等差数列的通项公式．‎ ‎【分析】利用等差数列的通项公式和前n项和公式，结合已知条件列出关于a1，d的方程组，解出a1，d，然后代入通项公式求解即可．‎ ‎【解答】解：设{an}的公差为d，首项为a1，由题意得 ‎，解得，‎ ‎∴a7=1+6×2=13，‎ 故选B．‎ ‎　‎ ‎4．已知a，b都是实数，那么“a2＞b2”是“a＞b”的（　　）‎ A．充分而不必要条件 B．必要而不充分条件 C．充分必要条件 D．既不充分也不必要条件 ‎【考点】必要条件、充分条件与充要条件的判断．‎ ‎【分析】首先由于“a2＞b2”不能推出“a＞b”；反之，由“a＞b”也不能推出“a2＞b2”．故“a2＞b2”是“a＞b”的既不充分也不必要条件．‎ ‎【解答】解：∵“a2＞b2”既不能推出“a＞b”；‎ 反之，由“a＞b”也不能推出“a2＞b2”．‎ ‎∴“a2＞b2”是“a＞b”的既不充分也不必要条件．‎ 故选D．‎ ‎　‎ ‎5．已知椭圆+=1上一点P到椭圆的一个焦点的距离为3，则点P到另一个焦点的距离为（　　）‎ A．2 B．3 C．5 D．7‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】先根据条件求出a=5；再根据椭圆定义得到关于所求距离d的等式即可得到结论．‎ ‎【解答】解：设所求距离为d，由题得：a=5．‎ 根据椭圆的定义得：2a=3+d⇒d=2a﹣3=7．‎ 故选D．‎ ‎　‎ ‎6．已知命题p：∃x∈R，x2﹣3x+3≤0，则（　　）‎ A．￢p：∃x∈R，x2﹣3x+3＞0，且￢p为真命题 B．￢p：∃x∈R，x2﹣3x+3＞0，且￢p为假命题 C．￢p：∀x∈R，x2﹣3x+3＞0，且￢p为真命题 D．￢p：∀x∈R，x2﹣3x+3＞0，且￢p为假命题 ‎【考点】命题的否定．‎ ‎【分析】根据特称命题的否定是全称命题即可得到结论．‎ ‎【解答】解：∵命题p是特称命题，‎ ‎∴根据特称命题的否定是全称命题得：￢p：∀x∈R，x2﹣3x+3＞0，‎ ‎∵判别式△=9﹣4×3=9﹣12=﹣3＜0，‎ ‎∴x2﹣3x+3＞0恒成立，‎ 故￢p为真命题，‎ 故选：C ‎　‎ ‎7．在△ABC中，若∠A=60°，∠B=45°，BC=3，则AC=（　　）‎ A． B． C． D．‎ ‎【考点】正弦定理．‎ ‎【分析】结合已知，根据正弦定理，可求AC ‎【解答】解：根据正弦定理，，‎ 则 故选B ‎　‎ ‎8．给出计算的值的一个程序框图如图，其中判断框内应填入的条件是（　　）‎ A．i＞10 B．i＜10 C．i＞20 D．i＜20‎ ‎【考点】循环结构．‎ ‎【分析】结合框图得到i表示的实际意义，要求出所需要的和，只要循环10次即可，得到输出结果时“i”的值，得到判断框中的条件．‎ ‎【解答】解：根据框图，i﹣1表示加的项数 当加到时，总共经过了10次运算，则不能超过10次，‎ i﹣1=10执行“是”‎ 所以判断框中的条件是“i＞10”‎ 故选A ‎　‎ ‎9．某个容器的底部为圆柱，顶部为圆锥，其正视图如图所示，则这个容器的容积为 ‎（　　）‎ A． B． C．3πm3 D．12πm3‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】由题意，其容积即此几何体的体积，可分两部分来求，分别求出圆锥与圆柱的体积，再相加即可求出其容积 ‎【解答】解：顶部圆锥的高为1，其底面是半径为1的圆，故其体积为=‎ 下部圆柱高为2，其底面是半径为1的圆，故其体积为2×π×12=2π 故其体积是2π+=‎ 这个容器的容积为为 故选A．‎ ‎　‎ ‎10．规定记号“⊗”表示一种运算，即a⊗b=ab+a+b2（a，b为正实数），若1⊗k=3，则k=（　　）‎ A．﹣2 B．1 C．﹣2或1 D．2‎ ‎【考点】函数的值．‎ ‎【分析】根据定义建立关于k的等式，然后解方程，最后验证定义域即可求出所求．‎ ‎【解答】解：由a⊗b=ab+a+b2（a，b为正实数），‎ 若1⊗k=3，则k+1+k2=3，解得k=1或k=﹣2，‎ 但根据定义域可知k=﹣2舍去，‎ 故选B ‎　‎ 二、填空题：本大题共4小题，每小题5分，满分20分．‎ ‎11．若等比数列{an}满足a2a4=，则a1a32a5=　　．‎ ‎【考点】等比数列的性质．‎ ‎【分析】由等比数列{an}的性质可得=，再次利用等比数列的定义和性质可得．‎ ‎【解答】解：∵等比数列{an}满足=，则，‎ 故答案为．‎ ‎　‎ ‎12．若x、y∈R+，x+4y=40，则xy的最大值为　100　．‎ ‎【考点】基本不等式．‎ ‎【分析】利用基本不等式的性质即可求出．‎ ‎【解答】解：∵x、y∈R+，x+4y=40，‎ ‎∴40≥2，解得xy≤100，‎ 当且仅当x=4y=20，即x=20，y=5时取等号，‎ 因此xy的最大值为100，‎ 故答案为：100．‎ ‎　‎ ‎13．函数y=log5（6﹣x）的定义域是　（﹣∞，6）　．‎ ‎【考点】函数的定义域及其求法．‎ ‎【分析】由对数式的真数大于0求得答案．‎ ‎【解答】解：要使原函数有意义，则6﹣x＞0，解得x＜6．‎ ‎∴函数y=log5（6﹣x）的定义域是：（﹣∞，6）．‎ 故答案为：（﹣∞，6）．‎ ‎　‎ ‎14．已知焦点在x轴的椭圆的离心率为0.5，焦距是2，则椭圆的标准方程是　+=1　．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】根据题意，设要求椭圆的方程为+=1，由椭圆的焦距为2，可得a2﹣b2=1①，又由其离心率为0.5，分析可得=②，联立两式解可得a2、b2的值，将a2、b2的值代入椭圆的方程计算可得答案．‎ ‎【解答】解：根据题意，要求椭圆的焦点在x轴上，则设其方程为： +=1，‎ 若其焦距为2，则2c=2，即c=1，则有a2﹣b2=1，①‎ 又由其离心率为0.5，则有=，即=，②‎ 联立①、②解可得a2=4，b2=3，‎ 则要求椭圆的方程为： +=1；‎ 故答案为： +=1．‎ ‎　‎ 三、解答题：本大题共6小题，满分80分．（解答须写出文字说明、证明过程和演算步骤）．‎ ‎15．已知函数f（x）=sinx+cosx，x∈R ‎（Ⅰ）求f（x）的最小正周期；‎ ‎（Ⅱ） 若f（α）=，求sin2α的值．‎ ‎【考点】三角函数的周期性及其求法．‎ ‎【分析】（Ⅰ）利用辅助角公式将函数化为y=Asin（ωx+φ）的形式，再利用周期公式求函数的最小正周期．‎ ‎（Ⅱ）利用f（α）=结合二倍角即可求sin2α的值 ‎【解答】解：（Ⅰ）函数f（x）=sinx+cosx=sin（x）‎ ‎∴函数f（x）的最小正周期T=．‎ ‎（Ⅱ）∵f（α）=，即f（α）=sinα+cosα=‎ 又∵sin2α+cos2α=1，‎ ‎∴（sinα+cosα）2=‎ ‎∴1+2sinαcosα=，‎ sin2α=2sinαcosα=﹣．‎ 故f（α）=时sin2α的值为﹣．‎ ‎　‎ ‎16．一个口袋中装有大小相同的2个白球和3个黑球．‎ ‎（1）采取不放回抽样方式，从中摸出两个球，写出所有的基本事件；‎ ‎（2）采取放回抽样方式，从中摸出两个球，求两球恰好颜色不同的概率．‎ ‎【考点】列举法计算基本事件数及事件发生的概率．‎ ‎【分析】（1）本题是一个等可能事件的概率，摸出两个球共有方法C52种，其中两球一白一黑有C21•C31种，得到概率．‎ ‎（2）摸出一球得白球的概率为=0.4，摸出一球得黑球的概率为=0.6，“放回后再摸一次，两球颜色不同”指“先白再黑”或“先黑再白”，这两种情况是互斥的，得到概率．‎ ‎【解答】解：（1）由题意知本题是一个等可能事件的概率 记“摸出两个球，两球恰好颜色不同”为A，‎ 摸出两个球共有方法C52=10种，‎ 其中两球一白一黑有C21•C31=6种．‎ ‎∴P（A）==；‎ ‎（2）记摸出一球，放回后再摸出一个球“两球恰好颜色不同”为B，‎ 摸出一球得白球的概率为=0.4，摸出一球得黑球的概率为=0.6，‎ ‎“放回后再摸一次，两球颜色不同”指“先白再黑”或“先黑再白”，这两种情况是互斥的，‎ ‎∴P（B）=0.4×0.6+0.6×0.4=0.48．‎ ‎　‎ ‎17．设x，y满足约束条件则z=2x+y的最大值为　11　．‎ ‎【考点】简单线性规划．‎ ‎【分析】先根据约束条件画出可行域，设z=2x+y，再利用z的几何意义求最值，只需求出直线2x+y=z过可行域内的点A时，从而得到z最大值即可．‎ ‎【解答】解：先根据约束条件画出可行域，易知可行域为一个四角形，‎ 其四个顶点分别为（0，0），（0，2），（2，0），（3，5），‎ 设z=2x+y，将最大值转化为y轴上的截距，‎ 当直线z=2x+y经过直线x﹣y+2=0与直线5x﹣y﹣10=0的交点A（3，5）时，z最大，‎ 故填：11．‎ ‎　‎ ‎18．在长方体ABCD﹣A1B1C1D1中，已知AB=BC=2，BB1=3，连接BC1，过B1作B1E⊥BC1交CC1于点E．‎ ‎（1）求证：B1E⊥平面ABC1；‎ ‎（2）求三棱锥C1﹣B1D1E的体积．‎ ‎【考点】棱柱、棱锥、棱台的体积；直线与平面垂直的判定．‎ ‎【分析】（1）由ABCD﹣A1B1C1D1为长方体，可得AB⊥B1E，又B1E⊥BC1，且AB∩BC1=B，由线面垂直的判定可得B1E⊥平面ABC1；‎ ‎（2）在长方形BCC1B1 中，由B1E⊥BC1，可得△C1B1B∽△EC1B1，结合已知求得，得到△B1C1E的面积，再由等积法求得三棱锥C1﹣B1D1E的体积．‎ ‎【解答】（1）证明：∵ABCD﹣A1B1C1D1为长方体，‎ ‎∴AB⊥平面BCC1B1，又B1E⊂平面BCC1B1，‎ ‎∴AB⊥B1E，又B1E⊥BC1，且AB∩BC1=B，‎ ‎∴B1E⊥平面ABC1；‎ ‎（2）解：在长方形BCC1B1 中，由B1E⊥BC1，‎ 可得△C1B1B∽△EC1B1，∵AB=BC=2，BB1=3，‎ ‎∴，得，‎ ‎∴，‎ ‎∴=．‎ ‎　‎ ‎19．若数列{an}的前n项和Sn=n2﹣10n（n=1，2，3，…），‎ ‎（1）求a1，a2的值；‎ ‎（2）求此数列的通项公式．‎ ‎【考点】数列递推式．‎ ‎【分析】（1）分别令n=1，n=2即可求出答案，‎ ‎（2）由题意可得：当n≥2时，an=Sn﹣Sn﹣1=2n﹣11．当n=1时，a1=S1=﹣9，也符合an=2n﹣11，进而求出数列的通项公式．‎ ‎【解答】解：（1）a1=S1=12﹣10=﹣9，a2=S2﹣S1=22﹣20+9=﹣7；‎ ‎（2）由题意可得：当n≥2时，Sn﹣1=（n﹣1）2﹣10（n﹣1）=n2﹣12n+11，‎ 所以an=Sn﹣Sn﹣1=2n﹣11．‎ 当n=1时，a1=S1=﹣9，也符合an=2n﹣11，‎ 所以数列的通项公式为：an=2n﹣11．‎ ‎　‎ ‎20．在平面直角坐标系xoy中，已知椭圆C1： =1（a＞b＞0）的左焦点F1（﹣5，0），且点P（0，12）在C1上．‎ ‎（1）求C1的方程；‎ ‎（2）若点M到椭圆C1的左焦点与右焦点的距离之比为2：3，求点M的坐标（x，y）满足的方程．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）由椭圆的焦点在x轴上，则b=12，c=5，a2=b2+c2=169，即可求得C1的方程；‎ ‎（2）由题意，利用两点之间得距离公式，化简整理即可求得M的坐标（x，y）满足的方程．‎ ‎【解答】解：（1）由题意可知：椭圆的焦点在x轴上，则b=12，c=5，‎ 则a2=b2+c2=169，‎ ‎∴C1的方程；‎ ‎（2）由F1（﹣5，0），F2（5，0），由=，‎ 则9丨MF1丨2=4丨MF2丨2，即9（x+5）2+9y2=4（x﹣5）2+4y2，‎ 整理得：（x+13）2+y2=144，‎ 点M的坐标（x，y）满足的方程（x+13）2+y2=144．‎ ‎　‎ ‎2017年4月18日