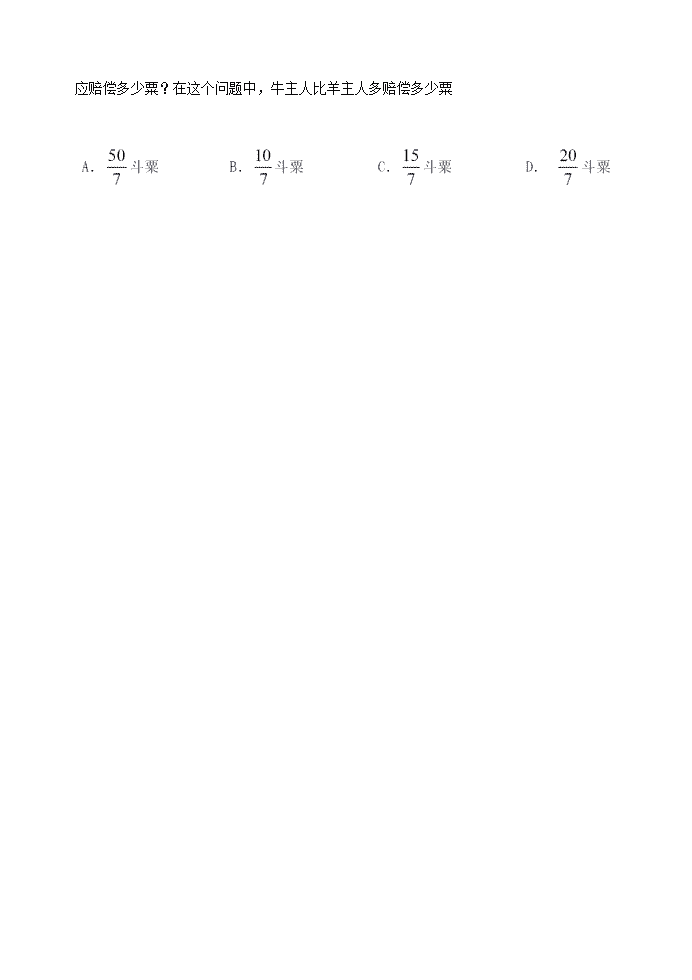宁夏石嘴山市第三中学2020届高三高考第五次模拟考试数学（理）试题 20页

石嘴山三中 2020 届高三年级第五次模拟考试 数学（理科）试卷 注意事项： ‎ ‎1．答题前，考生先将自己的姓名、准考证号码填写清楚，将条形码准确粘贴在考生信 息条形码粘贴区。 ‎ ‎2．选择题必须使用 2B 铅笔填涂；非选择题必须使用 0.5 毫米黑色字迹的签字笔书写，‎ 字体工整、笔迹清楚。 ‎ ‎3．请按照题号顺序在答题卡各题目的答题区域内作答，超出答题区域书写的答案无效。‎ ‎4．作图可先使用铅笔画出，确定后必须用黑色字迹的签字笔描黑。‎ ‎5．保持卡面清洁，不要折叠，不要弄破、弄皱，不准使用涂改液、修正带、刮纸刀。‎ 一. 选择题：本题共 12 小题，每小题 5 分，共 60 分，在每小题给出的四个选项中，只有一项是符合题目要求的。 ‎ ‎1．已知集合 A = {-1, 0,1, 2}, B = {x | e x ³ 1, x Î R }，则 A I B = A． {0,1, 2} B． {1, 2} C．{-1}‎ 2 已知(1- 2i ) z = 1+ i ，其中i 是虚数单位，则 z = ‎D．{2}‎ A． 10‎ ‎5‎ ‎B． 5 C． D．‎ ‎5‎ ‎3.下列四个命题中真命题的个数是 ‎(1)“ x = 1”是“ x2 - 3x + 2 = 0 ”的充分不必要条件 ‎(2)命题“ "x Î R ， sin x £ 1”的否定是“ $x Î R ， sin x > 1” (3)“若 am2 < bm2 ，则 a < b ”的逆命题为真命题 ‎(4)命题 p : "x Î[1, +¥ )， lg x ³ 0 ，命题 q : $x Î R ， x2 + x + 1 < 0 ，则 p Ú q 为真命题 A． 0 B．1 C． 2 D． 3 ‎ ‎4．2020 年春节突如其来的新型冠状病毒肺炎在湖北爆发，一方有难八方支援，全国各地的白衣天使走上战场的第一线，某医院抽调甲、乙两名医生，抽调 A 、 B 、C 三名护士支援武汉第一医院与第二医院，参加武汉疫情狙击战其中选一名护士与一名医生去第一医院，其它都在第二医院工作，则医生甲和护士 A 被选在第一医院工作的概率为 ‎1 1 1 1‎ A． B． C． D．‎ ‎12 6 5 9‎ ‎5．设a， b是两个不同的平面，m，n是两条不同的直线，下列说法正确的是 A．若 m//n ， m//a，则 n//a B．若 m ^ n ， m ^a， n //b，则a//b C．若 m Ì a， n Ì b， m//n ，则a//b D．若 n Ì a， m//n ， m ^ b，则a^ b ‎6．《九章算术》中有一题：今有牛、马、羊食人苗，苗主责之粟五斗，羊主曰：“我羊食半马”，马主曰：“我马食半牛”，今欲衰偿之，问各处儿何？其意思是：今有牛、马、 羊吃了别人的禾苗，禾苗主人要求赔偿五斗粟，羊主人说：“我羊所吃的禾苗只有马的一半”马主人说：“我马所吃的禾苗只有牛一半”．若按此比例偿还，牛、马、羊的主人各 应赔偿多少粟？在这个问题中，牛主人比羊主人多赔偿多少粟 ‎7.在三角形 ABC 中，a ，b ，c 分别为角 A ，B ，C 的对边，且满足 ‎ ‎ 二、填空题（本题共4小题，每小题5分，共20分）‎ ‎13. 已知，，则________．‎ ‎14．已知点，，过的直线与抛物线相交于两点．若为中点，‎ 则_______．‎ ‎15.若的展开式中常数项为，则直线，，轴与曲线围成的封闭图形的面积为　　　　　‎ ‎16．对于函数．现有下列结论：①任取，，都有；②函数有3个零点；③函数在上单调递增；④若关于的方程有且只有两个不同的实根，，则．其中正确结论的序号为______．（写出所有正确命题的序号）‎ 三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)‎ ‎17．（本小题满分12分）已知数列满足：，.‎ ‎（1）求及通项；‎ ‎（2）设是数列的前n项和，则数列，，，……中哪一项最小？并求出这个最小值.‎ ‎（3）求数列的前10项和 ‎18、（本小题满分12分）‎ 如图，在直三棱柱中，，，，分别是，中点，为线段上的一个动点.‎ ‎（1）证明：平面；‎ ‎（2）当二面角的余弦值为时，证明：.‎ ‎19．（本小题满分12分）2019年春节期间，某超市准备举办一次有奖促销活动，若顾客一次消费达到400元则可参加一次抽奖活动，超市设计了两种抽奖方案.‎ 方案一：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得60元的返金券，若抽到白球则获得20元的返金券，且顾客有放回地抽取3次.‎ 方案二：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得80元的返金券，若抽到白球则未中奖，且顾客有放回地抽取3次.‎ ‎（1）现有两位顾客均获得抽奖机会，且都按方案一抽奖，试求这两位顾客均获得180元返金券的概率；‎ ‎（2）若某顾客获得抽奖机会.‎ ‎①试分别计算他选择两种抽奖方案最终获得返金券的数学期望；‎ ‎②为了吸引顾客消费，让顾客获得更多金额的返金券，该超市应选择哪一种抽奖方案进行促销活动？‎ ‎20．（本小题满分12分）‎ 已知点是曲线C：上任意一点，，点在轴上的射影是C，.‎ ‎（1）求动点的轨迹方程；‎ ‎（2）过点的直线交点的轨迹于点，交点的轨迹于点，求的最大值.‎ ‎21. （本小题满分12分）‎ 已知函数．‎ Ⅰ若函数的最大值为3，求实数的值；‎ Ⅱ若当时，恒成立，求实数的取值范围；‎ Ⅲ若，是函数的两个零点，且，求证：．‎ 请考生在22，23，题中任选一题作答，如果多做，则按所做的第一题记分．做答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．‎ ‎22、（本小题满分10分）选修4-4：坐标系与参数方程 在新中国成立周年国庆阅兵庆典中，众多群众在脸上贴着一颗红心，以此表达对祖国的热爱之情.在数学中，有多种方程都可以表示心型曲线，其中有著名的笛卡尔心型曲线.如图，在直角坐标系中，以原点为极点，轴正半轴为极轴建立极坐标系。图中的曲线就是笛卡尔心型曲线，其极坐标方程为（），为该曲线上的任意一点.‎ ‎（1）当时，求点的极坐标；‎ ‎（2）将射线绕原点逆时针旋转与该曲线相交于点，求的最大值.‎ ‎23．（本题满分10分）选修4-5不等式选讲 已知函数．‎ ‎（Ⅰ）解不等式；‎ ‎（Ⅱ）已知，求证：．‎ 石嘴山三中2020届高三年级第五次模拟考试 数学(理科)试卷答案 ‎ 一、 选择题：‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A A D B D C D B A B D C 二． 填空题 13. ‎________ 14.________ 15.________ 16.__①②④ ‎ 三、解答题:(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)‎ ‎17．（本小题满分12分）已知数列满足：，.‎ ‎（1）求及通项；‎ ‎（2）设是数列的前n项和，则数列，，，……中哪一项最小？并求出这个最小值.‎ ‎（3）求数列的前10项和 ‎【详解】‎ ‎（1），当时，，，，.‎ ‎，故数列为首项是，公差为的等差数列，故.‎ ‎（2），故，，故最小，‎ ‎.‎ ‎(3)‎ ‎18、（本小题满分12分）‎ 如图，在直三棱柱中，，，，分别是，中点，为线段上的一个动点.‎ ‎（1）证明：平面；‎ ‎（2）当二面角的余弦值为时，证明：.‎ ‎【详解】‎ ‎（1）如图，取中点，连，‎ 因为是的中点，所以，‎ 在直三棱柱中，，‎ 因为是中点，所以，‎ 所以四边形为平行四边形，，‎ 因为平面，平面，‎ 所以平面；‎ ‎（2）不妨设，如图建立空间直角坐标系，‎ 设，，，，‎ 所以，‎ 设平面的一个法向量为，‎ 则，即，令，‎ 所以平面的一个法向量，‎ 平面的一个法向量，‎ 所以，‎ 此时，，‎ 所以，即.‎ ‎19．（本小题满分12分）2019年春节期间，某超市准备举办一次有奖促销活动，若顾客一次消费达到400元则可参加一次抽奖活动，超市设计了两种抽奖方案.‎ 方案一：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得60元的返金券，若抽到白球则获得20元的返金券，且顾客有放回地抽取3次.‎ 方案二：一个不透明的盒子中装有30个质地均匀且大小相同的小球，其中10个红球，20个白球，搅拌均匀后，顾客从中随机抽取一个球，若抽到红球则顾客获得80元的返金券，若抽到白球则未中奖，且顾客有放回地抽取3次.‎ ‎（1）现有两位顾客均获得抽奖机会，且都按方案一抽奖，试求这两位顾客均获得180元返金券的概率；‎ ‎（2）若某顾客获得抽奖机会.‎ ‎①试分别计算他选择两种抽奖方案最终获得返金券的数学期望；‎ ‎②为了吸引顾客消费，让顾客获得更多金额的返金券，该超市应选择哪一种抽奖方案进行促销活动？‎ ‎【详解】‎ ‎（1）选择方案一，则每一次摸到红球的概率为 设“每位顾客获得180元返金劵”为事件A，则 所以两位顾客均获得180元返金劵的概率 ‎（2）①若选择抽奖方案一，则每一次摸到红球的概率为，每一次摸到白球的概率为.‎ 设获得返金劵金额为元，则可能的取值为60，100，140，180.‎ 则；‎ ‎；‎ ‎；‎ ‎.‎ 所以选择抽奖方案一，该顾客获得返金劵金额的数学期望为 ‎（元）‎ 若选择抽奖方案二，设三次摸球的过程中，摸到红球的次数为，最终获得返金劵的金额为元，则，故 所以选择抽奖方案二，该顾客获得返金劵金额的 数学期望为（元）.‎ ‎② 即，所以该超市应选择第一种抽奖方案 ‎20．（本小题满分12分）‎ 已知点是曲线C：上任意一点，，点在轴上的射影是C，.‎ ‎（1）求动点的轨迹方程；‎ ‎（2）过点的直线交点的轨迹于点，交点的轨迹于点，求的最大值.‎ ‎【详解】‎ ‎（1）设，‎ 因为点到两点的距离之和为4，即 ‎ 可得点的轨迹是以为焦点，长轴长为4的椭圆，‎ 所以，即，且，则，‎ 所以点的轨迹方程是.‎ 设点坐标为，因所以点的坐标为，可得，‎ 化简得点的轨迹方程为.‎ ‎（2）若轴，则，.‎ 若直线不与轴垂直，设直线的方程为，即，‎ 则坐标原点到直线的距离，‎ ‎.‎ 设.将代入，并化简得，‎ ‎.‎ ‎，.‎ ‎，‎ 当且仅当即时，等号成立.‎ 综上所述，最大值为1.‎ ‎21. （本小题满分12分）‎ 已知函数．‎ Ⅰ若函数的最大值为3，求实数的值；‎ Ⅱ若当时，恒成立，求实数的取值范围；‎ Ⅲ若，是函数的两个零点，且，求证：．‎ ‎【详解】‎ Ⅰ函数的定义域为 因为，‎ 所以在内，，单调递增；‎ 在内，，单调递减．‎ 所以函数在处取得唯一的极大值，即的最大值．‎ 因为函数的最大值为3，‎ 所以，‎ 解得        ‎ Ⅱ因为当时，恒成立，‎ 所以，‎ 所以，‎ 即．令，‎ 则   ‎ 因为，‎ 所以．‎ 所以在单调递增 ‎ 所以，‎ 所以 ，‎ 所以即实数k的取值范围是；‎ Ⅲ由Ⅰ可知：，．‎ 所以     ‎ 因为，是函数的两个零点，‎ 所以．‎ 因为   ‎ 令，‎ 则．‎ 所以在，，单调递减．‎ 所以．‎ 所以，即．‎ 由Ⅰ知，在单调递增，‎ 所以，‎ 所以 请考生在22，23，题中任选一题作答，如果多做，则按所做的第一题记分．做答时，用2B铅笔在答题卡上把所选题目对应的标号涂黑．‎ ‎22、（本小题满分10分）选修4-4：坐标系与参数方程 在新中国成立周年国庆阅兵庆典中，众多群众在脸上贴着一颗红心，以此表达对祖国的热爱之情.在数学中，有多种方程都可以表示心型曲线，其中有著名的笛卡尔心型曲线.如图，在直角坐标系中，以原点为极点，轴正半轴为极轴建立极坐标系。图中的曲线就是笛卡尔心型曲线，其极坐标方程为（），为该曲线上的任意一点.‎ ‎（1）当时，求点的极坐标；‎ ‎（2）将射线绕原点逆时针旋转与该曲线相交于点，求的最大值.‎ ‎【解析】（1）设点在极坐标系中的坐标，由，得，，，或，所以点的极坐标为或.‎ ‎（2）由题意可设，.由，得，.‎ ‎,故时，的最大值为.‎ ‎23．（本题满分10分）选修4-5不等式选讲 已知函数．‎ ‎（Ⅰ）解不等式；‎ ‎（Ⅱ）已知，求证：．‎ ‎【详解】‎ ‎（Ⅰ），即为，‎ 该不等式等价于如下不等式组：‎ ‎1） ，‎ ‎2） ，‎ ‎3），‎ 所以原不等式的解集为或；‎ ‎（Ⅱ），‎ ‎，‎ 所以.‎