湖南省衡阳市第八中学2020届高三上学期第三次月考试题（10月）文科数学 9页

秘密 　 ★　 启用前 衡阳市八中 ２０２０ 届高三月考试题（三） 数学（文科） 注意事项： １ư 答题前，考生务必将自己的姓名、准考证号写在答题卡上，并认真核对条形码上的姓 名、准考证号和科目。 ２ư 考生作答时，选择题和非选择题均须作在答题卡上，在本试题卷上答题无效。 考生在 答题卡上按答题卡中注意事项的要求答题。 ３ư 考试结束后，将本试题卷和答题卡一并交回。 ４ư 本试题卷共 ４ 页。 如缺页，考生须声明，否则后果自负。 ５ư 时量 １２０ 分钟，满分 １５０ 分。 一、选择题（本大题共 １２ 小题，每小题 ５ 分，共 ６０ 分 ư 在每小题给出的四个选项中，只有一项 是符合题目要求的） １ư 已知集合 Ａ ＝ ｛０，１，２｝，Ａ 的非空子集个数为（　 　 ） Ａư ５　 　 　 　 　 　 　 　 Ｂư ６　 　 　 　 　 　 　 　 Ｃư ７　 　 　 　 　 　 　 　 Ｄư ８ ２ư 已知 ａ，ｂ∈Ｒ，ｉ 为虚数单位，（２ａ ＋ ｉ）（１ ＋ ３ｉ） ＝ ３ ＋ ｂｉ，则 ａ ＋ ｂ ＝ （　 　 ） Ａư ２２ Ｂư － １６ Ｃư ９ Ｄư － ９ ３ư 已知具有线性相关的变量 ｘ，ｙ，设其样本点为 Ａｉ （ｘｉ ，ｙｉ ）（ｉ ＝ １，２，……，６），回归直线方程为 ｙ ＝ ｘ ３ ＋ ｂ，若ＯＡ １ → ＋ ＯＡ ２ → ＋ … ＋ ＯＡ ６ → ＝ （９，６）（Ｏ 为坐标原点），则 ｂ ＝ （　 　 ） Ａư ３ Ｂư － ４ ３ Ｃư １ ２ Ｄư － １ ２ ４ư 已知平面向量ａ→ ，ｂ→满足｜ ａ→ ｜ ＝ ｜ ｂ→ ｜ ＝ １，若｜３ ａ→ ＋ ２ ｂ→ ｜ ＝ ７，则向量ａ→与ｂ→的夹角为（　 　 ） Ａư ３０° Ｂư ４５° Ｃư ６０° Ｄư １２０° —数学（文科）月考试卷（三）　 第 １ 页（共 ４ 页）— 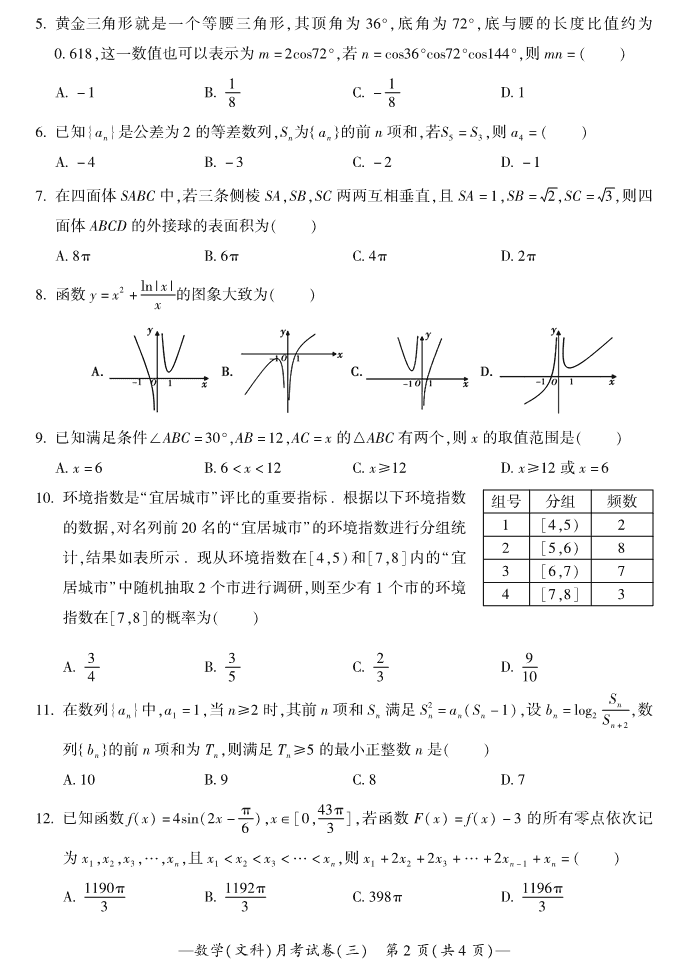５ư 黄金三角形就是一个等腰三角形，其顶角为 ３６°，底角为 ７２°，底与腰的长度比值约为 ０ư ６１８，这一数值也可以表示为 ｍ ＝ ２ｃｏｓ７２°，若 ｎ ＝ ｃｏｓ３６°ｃｏｓ７２°ｃｏｓ１４４°，则 ｍｎ ＝ （　 　 ） Ａư － １ Ｂư １ ８ Ｃư － １ ８ Ｄư １ ６ư 已知｛ａｎ ｝是公差为 ２ 的等差数列，Ｓｎ 为 ａｎ{ }的前 ｎ 项和，若Ｓ ５ ＝ Ｓ ３ ，则 ａ ４ ＝ （　 　 ） Ａư － ４ Ｂư － ３ Ｃư － ２ Ｄư － １ ７ư 在四面体 ＳＡＢＣ 中，若三条侧棱 ＳＡ，ＳＢ，ＳＣ 两两互相垂直，且 ＳＡ ＝ １，ＳＢ ＝ ２，ＳＣ ＝ ３，则四 面体 ＡＢＣＤ 的外接球的表面积为（　 　 ） Ａư ８π Ｂư ６π Ｃư ４π Ｄư ２π ８ư 函数 ｙ ＝ ｘ２ ＋ ｌｎ ｜ ｘ ｜ｘ 的图象大致为（　 　 ） ９ư 已知满足条件∠ＡＢＣ ＝ ３０°，ＡＢ ＝ １２，ＡＣ ＝ ｘ 的△ＡＢＣ 有两个，则 ｘ 的取值范围是（　 　 ） Ａư ｘ ＝ ６ Ｂư ６ ＜ ｘ ＜ １２ Ｃư ｘ≥１２ Ｄư ｘ≥１２ 或 ｘ ＝ ６ １０ư 环境指数是“宜居城市”评比的重要指标 ư 根据以下环境指数 的数据，对名列前 ２０ 名的“宜居城市”的环境指数进行分组统 计，结果如表所示 ư 现从环境指数在［４，５）和［７，８］内的“宜 居城市”中随机抽取 ２ 个市进行调研，则至少有 １ 个市的环境 指数在［７，８］的概率为（　 　 ） 组号 分组 频数 １ ［４，５） ２ ２ ［５，６） ８ ３ ［６，７） ７ ４ ［７，８］ ３ Ａư ３ ４ Ｂư ３ ５ Ｃư ２ ３ Ｄư ９ １０ １１ư 在数列｛ａｎ ｝中，ａ １ ＝ １，当 ｎ≥２ 时，其前 ｎ 项和 Ｓｎ 满足 Ｓ２ｎ ＝ ａｎ （Ｓｎ － １），设 ｂｎ ＝ ｌｏｇ２ Ｓｎ Ｓｎ ＋ ２ ，数 列 ｂｎ{ }的前 ｎ 项和为 Ｔｎ ，则满足 Ｔｎ ≥５ 的最小正整数 ｎ 是（　 　 ） Ａư １０ Ｂư ９ Ｃư ８ Ｄư ７ １２ư 已知函数 ｆ（ｘ） ＝ ４ｓｉｎ（２ｘ － π ６ ），ｘ∈［０，４３π ３ ］，若函数 Ｆ（ｘ） ＝ ｆ（ｘ） － ３ 的所有零点依次记 为 ｘ １ ，ｘ ２ ，ｘ ３ ，…，ｘｎ ，且 ｘ １ ＜ ｘ ２ ＜ ｘ ３ ＜ … ＜ ｘｎ ，则 ｘ １ ＋ ２ｘ ２ ＋ ２ｘ ３ ＋ … ＋ ２ｘｎ － １ ＋ ｘｎ ＝ （　 　 ） Ａư １１９０π ３ Ｂư １１９２π ３ Ｃư ３９８π Ｄư １１９６π ３ —数学（文科）月考试卷（三）　 第 ２ 页（共 ４ 页）— 二、填空题（本大题共 ４ 小题，每小题 ５ 分，共 ２０ 分） １３ư 函数 ｆ（ｘ） ＝ ｌｏｇ １ ３ （ｘ － １）的定义域为　 　 　 　 　 ư １４ư 若函数 ｆ（ｘ） ＝ ｌｎｘ ＋ １ ２ ｘ２ ＋ ｅｘ ，则曲线 ｙ ＝ ｆ（ｘ）在点（１，ｆ（１））处的切线的方程为　 　 　 　 ư １５ư ２０１９ 年 １０ 月 １ 日，我国举行盛大的建国 ７０ 周年阅兵，能 被邀到现场观礼是无比的荣耀 ư 假设如图，在坡度为 １５° 的观礼台上，某一列座位与旗杆在同一个垂直于地面的平 面上，在该列的第一排和最后一排测得旗杆顶端的仰角分 别为 ６０°和 ３０°，且第一排和最后一排的距离为 １０ ６米，则 旗杆的高度为　 　 　 　 　 米 ư １６ư 已知函数 ｆ（ｘ）满足 ｆ（ｘ） ＋ １ ＝ １ｆ ｘ ＋ １ ( )，当 ０≤ｘ≤１ 时，ｆ（ｘ） ＝ ｘ，若方程 ｆ（ｘ） － ｍｘ － ｍ ＝ ０ ｘ∈ － １，１ ( ]( )有两个不同实数根，则实数 ｍ 的最大值是　 　 　 　 　 ư 三、解答题（共 ７０ 分 ư 解答应写出文字说明、证明过程或演算步骤 ư 第 １７ ～ ２１ 题为必考题，每 个试题考生都必须作答 ư 第 ２２、２３ 题为选考题，考生根据要求作答） （一）必考题：共 ６０ 分 ư １７ư （本小题满分 １２ 分）已知函数 ｆ（ｘ） ＝ ３ｓｉｎｘｃｏｓｘ ＋ １ ２ （ｓｉｎ ２ ｘ － ｃｏｓ ２ ｘ）（ｘ∈Ｒ）， （１）求 ｆ（ｘ）的单调递增区间 ư （２）在△ＡＢＣ 中，角 Ａ，Ｂ，Ｃ 所对的边分别为 ａ，ｂ，ｃ，若 ｆ（Ａ） ＝ １，ｃ ＝ １０，ｃｏｓＢ ＝ １ ７ ，求△ＡＢＣ 的中线 ＡＤ 的长 ư １８ư （本小题满分 １２ 分）已知｛ａｎ ｝的前 ｎ 项和 Ｓｎ ＝ ４ｎ － ｎ２ ＋ ３， （１）求数列｛ａｎ ｝的通项公式； （２）求数列 ６ － ａｎ ２ ｎ ＋ １{ }的前 ｎ 项和 Ｔｎư １９ư （本小题满分 １２ 分）如图，在梯形 ＡＢＣＤ 中，ＡＢ∥ＣＤ，ＡＤ ＝ ＤＣ ＝ ＣＢ，∠ＡＢＣ ＝ π ３ ，平面 ＡＣＦＥ⊥平面 ＡＢＣＤ，四边形 ＡＣＦＥ 是矩 形，ＡＥ ＝ ＡＤ，点 Ｍ 在线段 ＥＦ 上 ư （１）求证：ＢＣ⊥平面 ＡＣＦＥ； （２）若ＥＭ ＭＦ ＝ １ ２ ，求证：ＡＭ∥平面 ＢＤＦư —数学（文科）月考试卷（三）　 第 ３ 页（共 ４ 页）— 衡阳市八中 ２０２０ 届高三月考试题（三） 文科数学参考答案 一、选择题：本大题共 １２ 小题，每小题 ５ 分，在每小题给出的四个选项中，只有一项是符合题目 要求的 ư 题号 １ ２ ３ ４ ５ ６ ７ ８ ９ １０ １１ １２ 答案 Ｃ Ａ Ｃ Ｄ Ｃ Ｄ Ｂ Ｃ Ｂ Ｄ Ｄ Ａ １０ư 【答案】Ｄ 【解析】：环境指数［７，８］在内的“宜居城市” 记为 Ａ １ ，Ａ ２ ，Ａ ３ ；环境指数在［４，５） 内的“宜居 城市”记为 Ｂ １ ，Ｂ ２ư 从环境指数在［４，５）和［７，８］内的“宜居城市”中随机抽取 ２ 个市的所 有基本事件是：｛Ａ １ ，Ａ ２ ｝，｛Ａ １ ，Ａ ３ ｝，｛Ａ ２ ，Ａ ３ ｝，｛Ａ １ ，Ｂ １ ｝，｛Ａ １ ，Ｂ ２ ｝，｛Ａ ２ ，Ｂ １ ｝，｛Ａ ２ ，Ｂ ２ ｝，｛Ａ ３ ， Ｂ １ ｝，｛Ａ ３ ，Ｂ ２ ｝，｛Ｂ １ ，Ｂ ２ ｝，共 １０ 个 ư 其中，没有 １ 个市的环境指数在［７，８］内的基本事件是：｛Ｂ １ ，Ｂ ２ ｝，共 １ 个 ư 所以所求的概率 Ｐ ＝ １ － １ １０ ＝ ９ １０ư 二、填空题：本大题共 ４ 小题，每小题 ５ 分． １３ư 【答案】（１，２］ １４ư 【答案】ｙ ＝ （２ ＋ ｅ）ｘ － ３ ２ １５ư 【答案】３０ 【解析】设 ＣＤ ＝ ｘ 在△ＡＥＤ 中，ＡＥ ＝ １０ ６，ＤＥ ＝ ＤＣ ｓｉｎ６０° ＝ ｘ ｓｉｎ６０°， ∠ＤＡＥ ＝ ４５°，∠ＡＥＤ ＝ １０５°，∴ ∠ＡＤＥ ＝ ３０° 由正弦定理得 ＤＥ ｓｉｎ∠ＤＡＥ ＝ ＡＥ ｓｉｎ∠ＡＤＥ，∴ ｘ ｓｉｎ６０° ｓｉｎ４５° ＝ １０ ６ ｓｉｎ３０°， ∴ ｘ ＝ ３０ １６ư 【答案】 １ ２三、解答题：解答应写出文字说明、证明过程或演算步骤． １７ư 解（１）ｆ（ｘ） ＝ １ ２ （ － ｃｏｓ２ｘ ＋ ３ｓｉｎ２ｘ） ＝ ｓｉｎ ２ｘ － π ６ [ ]ư ２ 分…………………… 递增区间：［ － π ６ ＋ ｋπ， π ３ ＋ ｋπ］ ６ 分…………………………………………… １ （２）由（１）知，ｆ（ｘ） ＝ ｓｉｎ ２ｘ － π ６ [ ]， ∴ 在△ＡＢＣ 中 ｆ（Ａ） ＝ １，∴ ｓｉｎ ２Ａ － π ６ [ ] ＝ １， ∴ ２Ａ － π ６ ＝ π ２ ，∴ Ａ ＝ π ３ 又 ｃｏｓＢ ＝ １ ７ ，∴ ｓｉｎＢ ＝ ４ ３ ７ ， ∴ ｓｉｎＣ ＝ ｓｉｎ（Ａ ＋ Ｂ） ＝ ３ ２ × １ ７ ＋ １ ２ × ４ ３ ７ ＝ ５ ３ １４ ， 在△ＡＢＣ 中，由正弦定理 ｃ ｓｉｎＣ ＝ ａ ｓｉｎ Ａ，得 １０ ５ ３ １４ ＝ ａ ３ ２ ∴ ａ ＝ １４，∴ ＢＤ ＝ ７ư ８ 分………………………………………………………… 在△ＡＢＤ 中，由余弦定理得， ＡＤ２ ＝ ＡＢ２ ＋ ＢＤ２ － ２ＡＢ·ＢＤｃｏｓＢ ＝ １０ ２ ＋ ７ ２ － ２ × １０ × ７ × ｃｏｓＢ ＝ １２９ ， 因此△ＡＢＣ 的中线 ＡＤ ＝ １２９ư １２ 分………………………………………… １８ư 【解析】（１）当 ｎ≥２ 时，ａｎ ＝ Ｓｎ － Ｓｎ － １ ＝ ４ｎ － ｎ２ － ［４（ｎ － １） － （ｎ － １） ２ ］ ＝ ５ － ２ｎ ，……２ 分 当 ｎ ＝ １ 时，ａ １ ＝ Ｓ １ ＝ ６，∴ ａｎ ＝ ６，（ｎ ＝ １） ５ － ２ｎ，（ｎ≥２） { ư ４ 分………………………… （２） ６ － ａｎ ２ ｎ ＋ １{ }的前 ｎ 项和为 Ｔｎ 令 ｂｎ ＝ ６ － ａｎ ２ ｎ ＋ １ ＝ ０　 　 　 （ｎ ＝ １） ２ｎ ＋ １ ２ ｎ ＋ １ 　 （ｎ≥２） { ∴ ｎ ＝ １ 时，Ｔｎ ＝ ０ ６ 分…………………………………………………………… ｎ≥２ 时，Ｔｎ ＝ ５ ２ ３ ＋ ７ ２ ４ ＋ ９ ２ ５ ＋ … ＋ ２ｎ － １ ２ ｎ ＋ ２ｎ ＋ １ ２ ｎ ＋ １ 　 （１） １ ２ Ｔｎ ＝ ５ ２ ４ ＋ ７ ２ ５ ＋ ９ ２ ６ ＋ … ＋ ２ｎ － １ ２ ｎ ＋ １ ＋ ２ｎ ＋ １ ２ ｎ ＋ ２ 　 （２） ８ 分………………… （１） － （２）得 １ ２ Ｔｎ ＝ ５ ２ ３ ＋ ２ ２ ４ ＋ ２ ２ ５ ＋ … ＋ ２ ２ ｎ ＋ １ － ２ｎ ＋ １ ２ ｎ ＋ ２ １ ２ Ｔｎ ＝ ５ ８ ＋ ２（ １ ２ ４ ＋ １ ２ ５ ＋ … ＋ １ ２ ｎ ＋ １ ） － ２ｎ ＋ １ ２ ｎ ＋ ２ １ ２ Ｔｎ ＝ ５ ８ ＋ ２· １ ２ ４ ［１ － （ １ ２ ） ｎ － ２ ］ １ － １ ２ － ２ｎ ＋ １ ２ ｎ ＋ ２ ＝ ７ ８ － ２ｎ ＋ ５ ２ ｎ ＋ ２ Ｔｎ ＝ ７ ４ － ２ｎ ＋ ５ ２ ｎ ＋ １ １０ 分……………………………………………… 综上：Ｔｎ ＝ ０　 　 　 　 　 （ｎ ＝ １） ７ ４ － ２ｎ ＋ ５ ２ ｎ ＋ １ 　 （ｎ≥２） { １２ 分………………………………………… ２ １９ư 【解析】（１）在梯形 ＡＢＣＤ 中，∵ ＡＢ∥ＣＤ， ＡＤ ＝ ＣＤ ＝ ＣＢ ＝ ａ，∠ＡＢＣ ＝ ６０° ∴ 四边形 ＡＢＣＤ 是等腰梯形， 且∠ＤＣＡ ＝ ∠ＤＡＣ ＝ ３０°，∠ＤＣＢ ＝ １２０° ∴ ∠ＡＣＢ ＝ ∠ＤＣＢ － ∠ＤＣＡ ＝ ９０°∴ ＡＣ⊥ＢＣ 又∵ 平面 ＡＣＦＥ⊥平面 ＡＢＣＤ，交线为 ＡＣ， ∴ ＢＣ⊥平面 ＡＣＦＥ ６ 分………………………………………………………… （２）当 ＥＭ ＝ ３ ３ ａ 时，ＡＭ∥平面 ＢＤＦ， 在梯形 ＡＢＣＤ 中，设 ＡＣ∩ＢＤ ＝ Ｎ，连接 ＦＮ，则 ＣＮ∶ ＮＡ ＝ １∶ ２ ∵ ＥＭ ＝ ３ ３ ａ，而 ＥＦ ＝ ＡＣ ＝ ３ａ ∴ ＥＭ∶ ＭＦ ＝ １∶ ２ ， ∴ ＭＦ∥＝ 　 ＡＮ，∴ 四边形 ＡＮＦＭ 是平行四边形，∴ ＡＭ∥ＮＦ 又∵ ＮＦ⊂平面 ＢＤＦ，ＡＭ⊂／ 平面 ＢＤＦ ∴ ＡＭ∥平面 ＢＤＦ １２ 分………………… ２０ư 【解析】 （Ⅰ）设｜ Ｆ １ Ｆ ２ ｜ ＝ ２ｃ，由题意得 ｃ ａ ＝ ３ ２ １ ２ ·２ｃ· ｂ２ ａ ＝ ３ ２ ì î í ï ïï ï ï ∴ ａ ＝ ２，ｂ ＝ １， 故椭圆 Ｃ 的方程为ｘ２ ４ ＋ ｙ２ ＝ １ ４ 分…………………………………………… （Ⅱ）当直线 ｌ 的斜率存在时，设其直线方程为 ｙ ＝ ｋｘ ＋ ｍ，设 Ａ（ｘ １ ，ｙ １ ），Ｂ（ｘ ２ ，ｙ ２ ）， 联立议程组 ｙ ＝ ｋｘ ＋ ｍ ｘ２ ＋ ４ｙ２ ＝ ４ { ，整理得（４ｋ２ ＋ １）ｘ２ ＋ ８ｋｍｘ ＋ ４ｍ２ － ４ ＝ ０， 由方程的判别式 Δ ＞ ０ 得 ４ｋ２ － ｍ２ ＋ ２ ＞ ０　 　 　 　 （１） ６ 分………………… ｘ １ ＋ ｘ ２ ＝ － ８ｋｍ ４ｋ２ ＋ １，ｘ １ ｘ ２ ＝ ４ｍ２ － ４ ４ｋ２ ＋ １ ，由∠ＡＯＢ ＝ ９０°，得ＯＡ→·ＯＢ→ ＝ ０ 即 ｘ １ ｘ ２ ＋ ｙ １ ｙ ２ ＝ ０， 而 ｙ １ ｙ ２ ＝ （ｋ １ ｘ １ ＋ ｍ）（ｋ １ ｘ １ ＋ ｍ） ，则 ｘ １ ｘ ２ ＋ ｙ １ ｙ ２ ＝ （ｋ２ ＋ １）ｘ １ ｘ ２ ＋ ｍｋ（ｘ １ ＋ ｘ ２ ） ＋ ｍ２ ＝ ０， 所以（１ ＋ ｋ２ ）·４ｍ２ － ４ ４ｋ２ ＋ １ ＋ ｍｋ· － ８ｋｍ ４ｋ２ ＋ １ ＋ ｍ２ ＝ ０，整理得 ５ｍ２ － ４ｋ２ － ４ ＝ ０， 把 ４ｋ２ ＝ ５ｍ２ － ４ 代入（１）得 ｍ２ ＞ ３ ４ ， ８ 分……………………………………… 而 ４ｋ２ ＝ ５ｍ２ － ４≥０，∴ ｍ２ ≥ ４ ５ ，显然满足 ｍ２ ＞ ３ ４ ， 直线 ｌ 始终与圆 ｘ２ ＋ ｙ２ ＝ ｒ２ 相切，得圆心（０，０）到直线 ｌ 的距离 ｄ ＝ ｒ，则 ｒ２ ＝ ｄ２ ＝ ｍ２ １ ＋ ｋ２ ， 由 ｍ２ ＝ ４ ５ ｋ２ ＋ ４ ５ ，得 ｒ２ ＝ ４ ５ ，因为 ｒ ＞ ０，所以 ｒ ＝ ２ ５ ５ ； １０ 分………………… 当直线 ｌ 的斜率不存在时，若直线 ｌ 与圆 ｘ２ ＋ ｙ２ ＝ ４ ５ 相切，此时直线 ｌ 的方程为 ｘ ＝ ± ２ ５ ５ ， ３ ｒ ＝ ２ ５ ５ ư 综上所述 ｒ ＝ ２ ５ ５ １２ 分…………………………………………………………… ２１ư 【解析】（１）ｆ′（ｘ） ＝ ｆ′（１）·ｅ２ｘ － ２ ＋ ２ｘ － ２ｆ（０），令 ｘ ＝ １ 解得 ｆ（０） ＝ １， 由 ｆ（ｘ） ＝ ｆ′（１） ２ ·ｅ２ｘ － ２ ＋ ｘ２ － ２ｆ（０）ｘ，令 ｘ ＝ ０ 得 ｆ（０） ＝ ｆ′（１） ２ ｅ － ２ ，ｆ′（１） ＝ ２ｅ２ ， 所以 ｆ（ｘ） ＝ ｅ２ｘ － ２ｘ ＋ ｘ２ ư ２ 分…………………………………………………… （２）因为 ｆ（ｘ） ＝ ｅ２ｘ － ２ｘ ＋ ｘ２ ，所以 ｇ（ｘ） ＝ ｆ（ ｘ ２ ） － １ ４ ｘ２ ＋ （１ － ａ）ｘ ＋ ａ ＝ ｅｘ － ａ（ｘ － １） ， ｇ′（ｘ） ＝ ｅｘ － ａ， ①当 ａ≤０ 时，总有 ｇ′（ｘ） ＞ ０，函数 ｇ（ｘ）在 Ｒ 上单调递增； ４ 分……………… ②当 ａ ＞ ０ 时，由 ｇ′（ｘ） ＞ ０ 得函数 ｇ（ｘ）在（ｌｎａ， ＋ ∞ ）上单调递增，由 ｇ′（ｘ） ＜ ０ 得函数 ｇ （ｘ）在（ － ∞ ，ｌｎａ）上单调递减； 综上，当 ａ≤０ 时，总有 ｇ′（ｘ） ＞ ０，函数 ｇ（ｘ）在 Ｒ 上单调递增；当 ａ ＞ ０ 时， ｇ（ｘ）在（ｌｎａ， ＋ ∞ ）上单调递增，ｇ（ｘ）在（ － ∞ ，ｌｎａ）上单调递减 ư ６ 分……………………… （３）设 ｐ（ｘ） ＝ ｅ ｘ － ｌｎｘ，ｑ（ｘ） ＝ ｅｘ － １ － ｌｎｘ ＋ ３，ｐ′（ｘ） ＜ ０ 得 ｐ（ｘ）在［１， ＋ ∞ ］上递减，所以当 １≤ｘ≤ｅ 时，ｐ（ｘ）≥ｐ（ｅ） ＝ ０；当 ｘ ＞ ｅ 时，ｐ（ｘ） ＜ ０， 而 ｑ′（ｘ） ＝ ｅｘ － １ － １ｘ ，ｑｎ （ｘ） ＝ ｅｘ － １ ＋ １ｘ２ ＞ ０ ， 所以 ｑ′（ｘ）在［１， ＋ ∞ ）上递增，ｑ′（ｘ）≥ｑ′（１） ＝ ０ 则 ｑ（ｘ）在［１， ＋ ∞ ）上递增，ｑ（ｘ）≥ｑ（１） ＝ ４ ＞ ０ ①当 １≤ｘ≤ｅ 时，｜ ｐ（ｘ） ｜ － ｜ ｑ（ｘ） ｜ ＝ ｐ（ｘ） － ｑ（ｘ） ＝ ｅ ｘ － ｅｘ － １ － ３ ＝ ｍ（ｘ） ， ｍ（ｘ） ＝ － ｅ ｘ２ － ｅｘ － １ ＜ ０，∴ ｍ（ｘ）在［１， ＋ ∞ ）上递减， ｎ（ｘ）≤ｍ（１） ＝ ｅ － ４ ＜ ０，∴ ｜ ｐ（ｘ） ｜ ＜ ｜ ｑ（ｘ） ｜ ，所以 ｅ ｘ 比 ｅｘ － １ ＋ ３ 更靠近 ｌｎｘ；……８ 分 ②当 ｘ ＞ ｅ 时， ｜ ｐ（ｘ） ｜ － ｜ ｑ（ｘ） ｜ ＝ － ｐ（ｘ） － ｑ（ｘ） ＝ － ｅ ｘ ＋ ２ｌｎｘ － ｅｘ － １ － ３ ＜ ２ｌｎｘ － ｅｘ － １ － ３ ＝ ｎ（ｘ） ， ｎ′（ｘ） ＝ ２ｘ － ｅｘ － １ ，ｎ″（ｘ） ＝ － ２ｘ２ － ｅｘ － １ ＜ ０， 所以 ｎ′（ｘ） ＜ ｎ′（ｅ） ＜ ０，∴ ｎ（ｘ） 递减，ｎ（ｘ） ＜ ｎ（ｅ） ＜ ０， ｜ ｐ（ｘ） ｜ ＜ ｜ ｑ（ｘ） ｜ ， ｅ ｘ 比 ｅｘ － １ ＋ ３ 更靠近 ｌｎｘ ， １０ 分…………………………… 综上所述，当 ｘ≥１ 时， ｅ ｘ 比 ｅｘ － １ ＋ ３ 更靠近 ｌｎｘư １２ 分………………………… ４ ２２ư 【解析】（１）将 ｘ ＝ ２ － ２ ２ ｔ 代入 ｘ ＋ ｙ － ２ ＝ ０，得 ｙ ＝ ２ ２ ｔ， ∴ 直线 ｌ 的参数方程是 ｘ ＝ ２ － ２ ２ ｔ ｙ ＝ ２ ２ ｔ ì î í ï ïï ï ï （ｔ 为参数） ２ 分…………………………… 由 ρ（１ ＋ ｃｏｓ２θ） ＝ ２ａｓｉｎθ（ａ ＞ ０）得曲线 Ｃ 的直角坐标方程：ｘ２ ＝ ａｙ（ａ ＞ ０）…………５ 分 （２）将直线 ｌ 的参数方程代入 ｘ２ ＝ ａｙ，得：ｔ２ － ２（４ ＋ ａ）ｔ ＋ ８ ＝ ０， 设 Ａ、Ｂ 对应的参数分别是 ｔ １ ，ｔ ２ ，∴ ｔ １ ＋ ｔ ２ ＝ ２（４ ＋ ａ），ｔ １ ｔ ２ ＝ ８， ７ 分………… 由题意知：｜ ＡＢ ｜ ２ ＝ ｜ ＰＡ｜ ·｜ ＰＢ ｜ ，∴ ｜ ｔ １ － ｔ ２ ｜ ２ ＝ ｜ ｔ １ ｔ ２ ｜ ，∴ ｜ ｔ １ ＋ ｔ ２ ｜ ２ ＝ ４ｔ １ ｔ ２ ＋ ｜ ｔ １ ｔ ２ ｜ 得：２（４ ＋ ａ） ２ ＝ ４０，∴ ａ ＝ ± ２ ５ － ４，又∵ ａ ＞ ０，∴ ａ ＝ ２ ５ － ４ １０ 分………… 经检验：符合题意。 ２３ư 【解析】（１）ｆ（ｘ） ＝ － ３ｘ ＋ ４，ｘ ＜ １ － ｘ ＋ ２，１≤１≤ ３ ２ ３ｘ － ４，ｘ ＞ ３ ２ ì î í ï ïï ï ïï ， ２ 分…………………………………… 由 ｆ（ｘ）≤２ 得， ２ ３ ≤ｘ≤２，所求解集为［ ２ ３ ，２］ ５ 分…………………………… （２）ｇ（ｘ） ＝ ｜２ｘ － ２０２０ ＋ ａ ｜ ＋ ｜２ｘ － ２０１９ ｜ ≥｜ （２ｘ － ２０２０ ＋ ａ） － （２ｘ － ２０１９） ｜ ＝ ｜ ａ － １ ｜ ７ 分……………………………………………………………………… ｆ（ｘ）ｍｉｎ ＝ ｆ（ ３ ２ ） ＝ １ ２ ∴ １ ２ ≥｜ ａ － １ ｜ ∴ １ ２ ≤ａ≤ ３ ２ １０ 分………………………………………………………………… ５