数学理·湖北省荆、荆、襄、宜四地七校2016-2017学年高二上学期期中考试数学理试卷+Word版含解析x 21页

‎2016-2017学年湖北省荆、荆、襄、宜四地七校考试联盟联考高二（上）期中数学试卷（理科）‎ ‎　‎ 一、选择题 ‎1．在对16和12求最大公约数时，整个操作如下：16﹣12=4，12﹣4=8，8﹣4=4，由此可以看出12与16的最大公约数是（　　）‎ A．16 B．12 C．8 D．4‎ ‎2．已知全集U为R，集合A={x|x2＜4}，B=（x﹣2）}，则下列关系正确的是（　　）‎ A．A∪B=R B．A∪（∁∪B）=R C．（∁∪A）∪B=R D．A∩（∁∪B）=A ‎3．已知函数f（x）=2sin（ωx+）﹣1（ω＞0）的图象向右平移个单位后与原图象重合，则ω的最小值是（　　）‎ A．6 B．3 C． D．‎ ‎4．设l为直线，α，β为不同的平面，下列命题正确的是（　　）‎ A．若l∥α，l∥β，则α∥β 　B．若l∥α，α∥β，则l∥β C．若l⊥α，l∥β，则α⊥β　 D．若l⊥α，l⊥β，则α⊥β ‎5．直线xcosθ+y﹣1=0（θ∈R且θ≠kπ，k∈Z）与圆2x2+2y2=1的位置关系是（　　）‎ A．相交 B．相切 C．相离 D．无法确定 ‎6．在△OAB中，C为边AB上任意一点，D为OC上靠近O的一个三等分点，若=λ+μ，则λ+μ的值为（　　）‎ A． B． C． D．1‎ ‎7．已知函数f（x）=sinxcos2x，下列结论正确的是（　　）‎ A．y=f（x）的图象关于对称 B．y=f（x）的图象关于对称 C．y=f（x）的图象关于y轴对称 D．y=f（x）不是周期函数 ‎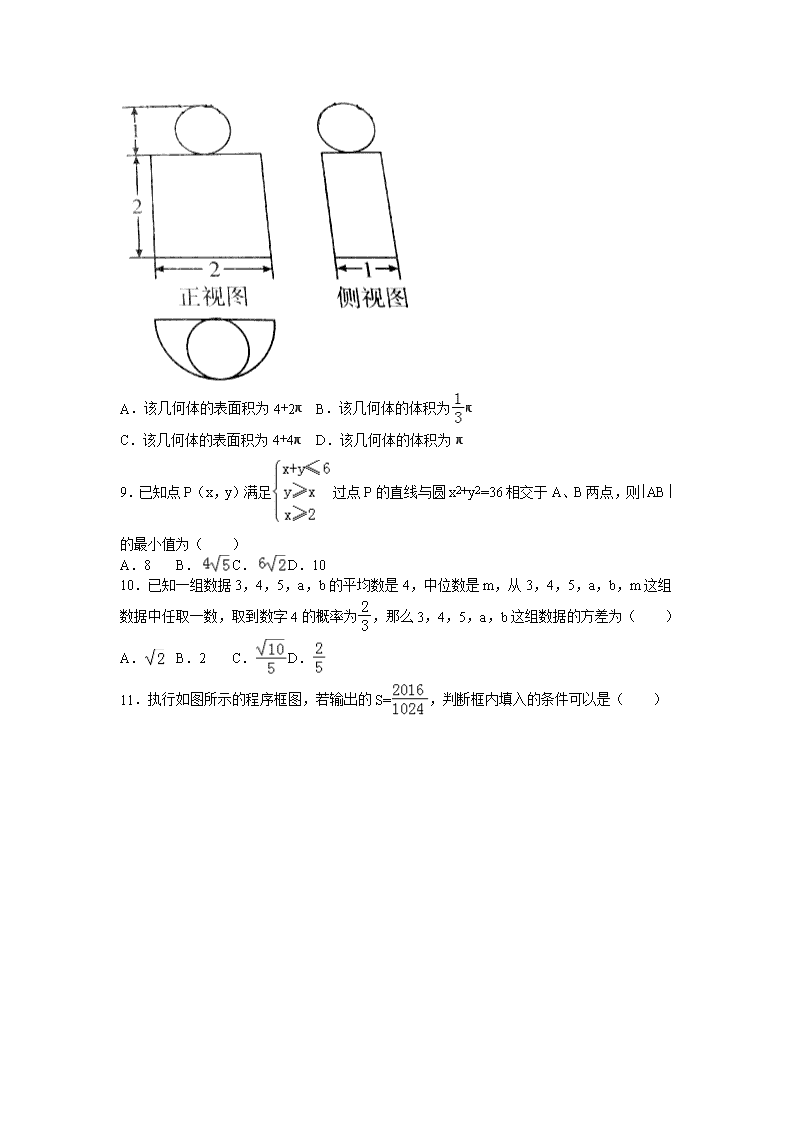8．已知某空间几何体的三视图如图所示，则（　　）‎ A．该几何体的表面积为4+2π B．该几何体的体积为π C．该几何体的表面积为4+4π D．该几何体的体积为π ‎9．已知点P（x，y）满足过点P的直线与圆x2+y2=36相交于A、B两点，则|AB|的最小值为（　　）‎ A．8 B． C． D．10‎ ‎10．已知一组数据3，4，5，a，b的平均数是4，中位数是m，从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，那么3，4，5，a，b这组数据的方差为（　　）‎ A． B．2 C． D．‎ ‎11．执行如图所示的程序框图，若输出的S=，判断框内填入的条件可以是（　　）‎ A．n＜10 B．n≤10 C．n≤1024 D．n＜1024‎ ‎12．钝角△OAB三边的比为2：2：（﹣），O为坐标原点，A（2，2）、B（a，a），则a的值为（　　）‎ A．2 B． C．2或 D．+‎ ‎　‎ 二、填空题 ‎13．直线2x+y﹣2=0被圆x2+y2=5截得的弦长为　　．‎ ‎14．已知θ服从上的均匀分布，则2|sinθ|＜成立的概率为　　．‎ ‎15．已知四面体P﹣ABC各面都是直角三角形，且最长棱长PC=2，则此四面体外接球的表面积为　　．‎ ‎16．记Min{a，b}为a、b两数中的最小值，当正数x，y变化时，令t=Min{4x+y，}，则t的最大值为　　．‎ ‎　‎ 三、解答题 ‎17．（12分）某小学对五年级的学生进行体质测试，已测得五年级一班30名学生的跳远成绩（单位：cm），用茎叶图统计如图，男生成绩在175cm以上（包括175cm）定义为合格，成绩在175cm以下（不含175cm）定义为“不合格”；女生成绩在165以上（包括165cm）定义为“合格”，成绩在165cm以下（不含165cm）定义为“不合格”．‎ ‎（1）求男生跳远成绩的中位数．‎ ‎（2）根据男女生的不同，用分层抽样的方法从该班学生中抽取1个容量为5的样本，求抽取的5人中女生的人数．‎ ‎（3）以此作为样本，估计该校五年级学生体质的合格率．‎ ‎18．（12分）已知函数f（x）=在（﹣1，+∞）是增函数．‎ ‎（1）当b=1时，求a的取值范围．‎ ‎（2）若g（x）=f（x）﹣1008没有零点，f（1）=0，求f（﹣3）的值．‎ ‎19．（12分）在数列{an}中，a1=1an+1=，n∈N*．‎ ‎（1）求证数列为等比数列．‎ ‎（2）求数列{an}的前n项和Sn．‎ ‎20．（12分）在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，∠APD=90°，PA=PD=AB=a，ABCD是矩形，E是PD的中点．‎ ‎（1）求证：PB⊥AC．‎ ‎（2）求二面角E﹣AC﹣D的正切值．‎ ‎21．（12分）已知圆C1：（x+2）2+（y﹣1）2=4与圆C2：（x﹣3）2+（y﹣4）2=4，过点P（﹣1，5）作两条互相垂直的直线l1：y=k（x+1）+5，l2：y=﹣（x+1）+5．‎ ‎（1）若k=2时，设l1与圆C1交于A、B两点，求经过A、B两点面积最小的圆的方程．‎ ‎（2）若l1与圆C1相交，求证：l2与圆C2相交，且l1被圆C1截得的弦长与l2被圆C2截得的弦长相等．‎ ‎（3）是否存在点Q，过Q的无数多对斜率之积为1的直线l3，l4，l3被圆C1截得的弦长与l4被圆C2截得的弦长相等．若存在求Q的坐标，若不存在，说明理由．‎ ‎22．（10分）在△ABC中，三个内角A，B，C所对的边分别为a，b，c，已知函数f（x）=sin（3x+B）+cos（3x+B）是偶函数，且b=f（）．‎ ‎（1）求b．‎ ‎（2）若a=，求角C．‎ ‎　‎ ‎2016-2017学年湖北省荆、荆、襄、宜四地七校考试联盟联考高二（上）期中数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．（2016秋•湖北期中）在对16和12求最大公约数时，整个操作如下：16﹣12=4，12﹣4=8，8﹣4=4，由此可以看出12与16的最大公约数是（　　）‎ A．16 B．12 C．8 D．4‎ ‎【考点】用辗转相除计算最大公约数．‎ ‎【专题】转化思想；算法和程序框图．‎ ‎【分析】利用“更相减损法”即可得出．‎ ‎【解答】解：在对16和12求最大公约数时，整个操作如下：16﹣12=4，12﹣4=8，8﹣4=4，‎ 由此可以看出12与16的最大公约数是4．‎ 故选：D．‎ ‎【点评】本题考查了更相减损法求两数的最大公约数，考查了推理能力与计算能力，属于基础题．‎ ‎　‎ ‎2．（2016秋•湖北期中）已知全集U为R，集合A={x|x2＜4}，B=（x﹣2）}，则下列关系正确的是（　　）‎ A．A∪B=R B．A∪（∁∪B）=R C．（∁∪A）∪B=R D．A∩（∁∪B）=A ‎【考点】交、并、补集的混合运算．‎ ‎【专题】集合思想；定义法；集合．‎ ‎【分析】化简集合A，B，求出它们的补集，再判断选项是否正确即可．‎ ‎【解答】解：全集U为R，集合A={x|x2＜4}={x|﹣2＜x＜2}，‎ B=（x﹣2）}={x|x﹣2＞0}={x|x＞2}，‎ A∪B={x|x＞﹣2且x≠2}，A错误；‎ ‎∁UB={x|x≤2}，A∪（∁UB）={x|x≤2}，B错误；‎ ‎∁UA={x|x≤﹣2或x≥2}，∴（∁UA）∪B={x|x≤﹣2或x≥2}，C错误；‎ A∩（∁UB）={x|﹣2＜x＜2}=A，D正确．‎ 故选：D．‎ ‎【点评】本题考查了集合的化简与运算问题，是基础题目．‎ ‎　‎ ‎3．（2016秋•湖北期中）已知函数f（x）=2sin（ωx+）﹣1（ω＞0）的图象向右平移个单位后与原图象重合，则ω的最小值是（　　）‎ A．6 B．3 C． D．‎ ‎【考点】函数y=Asin（ωx+φ）的图象变换．‎ ‎【专题】计算题；函数思想；三角函数的图像与性质．‎ ‎【分析】根据函数y=Asin（ωx+φ）的图象变换规律、函数y=Asin（ωx+φ）的周期性，可得ω的最小值．‎ ‎【解答】解：函数f（x）=2sin（ωx+）﹣1的图象向右平移个单位后，‎ 可得函数y=2sin[ω（x﹣）+]﹣1=sin（ωx+﹣）+1的图象．‎ 再根据所得图象与原图象重合，可得﹣=2kπ，k∈z．即ω=﹣6k，k∈Z，ω＞0‎ 则ω的最小值为，6‎ 故选：A．‎ ‎【点评】本题主要考查函数y=Asin（ωx+φ）的图象变换规律，函数y=Asin（ωx+φ）的周期，属于中档题．‎ ‎　‎ ‎4．（2016秋•湖北期中）设l为直线，α，β为不同的平面，下列命题正确的是（　　）‎ A．若l∥α，l∥β，则α∥β B．若l∥α，α∥β，则l∥β C．若l⊥α，l∥β，则α⊥β D．若l⊥α，l⊥β，则α⊥β ‎【考点】平面与平面之间的位置关系；空间中直线与平面之间的位置关系．‎ ‎【专题】转化法；空间位置关系与距离．‎ ‎【分析】由线面平行的性质判断A；由线面平行和面面平行的性质判断B；由线面垂直和线面平行的性质，结合面面垂直的判定定理，可判断C；由垂直于同一条直线的两平面平行，判断D．‎ ‎【解答】解：对于A，若l∥α，l∥β，则α∥β或α，β相交，故A错；‎ 对于B，若l∥α，α∥β，则l∥β或l⊂β，故B错；‎ 对于C，若l⊥α，l∥β，可过l作一个平面与β相交于m，则m∥l，且m⊥α，则α⊥β，故C正确；‎ 对于D，若l⊥α，l⊥β，则α∥β，故D错．‎ 故选：C．‎ ‎【点评】本题考查空间线面位置关系的判断，注意运用线面、面面平行或垂直的判定定理和性质定理，考查推理和空间想象能力，属于基础题．‎ ‎　‎ ‎5．（2011•嘉定区一模）直线xcosθ+y﹣1=0（θ∈R且θ≠kπ，k∈Z）与圆2x2+2y2=1的位置关系是（　　）‎ A．相交 B．相切 C．相离 D．无法确定 ‎【考点】直线与圆的位置关系．‎ ‎【专题】计算题．‎ ‎【分析】求出圆心（0，0）到直线xcosθ+y﹣1=0的距离等于 ，再由θ≠kπ，k∈Z，可得 cosθ≠±1，故 ＞，即 圆心（0，0）到直线xcosθ+y﹣1=0的距离大于半径，从而得出结论．‎ ‎【解答】解：圆2x2+2y2=1 即 x2+y2=，圆心（0，0）到直线xcosθ+y﹣1=0的距离等于 ，‎ 由于θ≠kπ，k∈Z，∴cosθ≠±1，∴＞，即 圆心（0，0）到直线xcosθ+y﹣1=0的距离大于半径，‎ 故直线和圆相离，‎ 故选C．‎ ‎【点评】本题主要考查直线和圆的位置关系，点到直线的距离公式，属于中档题．‎ ‎　‎ ‎6．（2016秋•湖北期中）在△OAB中，C为边AB上任意一点，D为OC上靠近O的一个三等分点，若=λ+μ，则λ+μ的值为（　　）‎ A． B． C． D．1‎ ‎【考点】向量在几何中的应用．‎ ‎【专题】转化思想；转化法；平面向量及应用．‎ ‎【分析】由已知可得=3λ+3μ，由C为边AB上任意一点，根据三点共线的充要条件，可得：3λ+3μ=1，进而得到答案．‎ ‎【解答】解：∵D为OC上靠近O的一个三等分点，‎ ‎∴3=，‎ 又∵=λ+μ，‎ ‎∴=3λ+3μ，‎ ‎∵C为边AB上任意一点，‎ ‎∴3λ+3μ=1，‎ 故λ+μ=，‎ 故选：B ‎【点评】本题考查的知识点是平面向量在几何中的应用，三点共线的充要条件，难度中档．‎ ‎　‎ ‎7．（2016秋•湖北期中）已知函数f（x）=sinxcos2x，下列结论正确的是（　　）‎ A．y=f（x）的图象关于对称 B．y=f（x）的图象关于对称 C．y=f（x）的图象关于y轴对称 D．y=f（x）不是周期函数 ‎【考点】正弦函数的对称性．‎ ‎【专题】转化思想；综合法；三角函数的图像与性质．‎ ‎【分析】根据题意逐一判断各个选项是否正确，从而得出结论．‎ ‎【解答】解：对于函数f（x）=sinxcos2x，‎ ‎∵f（π﹣x）=sin（π﹣x）cos2（π﹣x）=sinxcos2x=f（x），‎ ‎∴f（x）关于直线x=对称，故A正确，B不正确．‎ 根据f（﹣x）=﹣sinxcos2x=﹣f（x），故函数为奇函数，它的图象关于x轴对称，故排除C．‎ ‎∵f（x+2π）=sin（2π+x）cos2（2π+x）=sinxcos2x=f（x），‎ ‎∴2π是函数y=f（x）的周期，故D错误．‎ 故选：A．‎ ‎【点评】本题考查三角函数的对称性，考查了三角函数值域的解法，考查排除法在选择题中的应用，属于中档题．‎ ‎　‎ ‎8．（2016秋•湖北期中）已知某空间几何体的三视图如图所示，则（　　）‎ A．该几何体的表面积为4+2π B．该几何体的体积为π C．该几何体的表面积为4+4π D．该几何体的体积为π ‎【考点】由三视图求面积、体积．‎ ‎【专题】计算题；空间位置关系与距离．‎ ‎【分析】由三视图可知，该几何体为上部为半径为的球，下部为半径为1，高为2的半个圆柱，利用相关的面积公式求解即可解答．‎ ‎【解答】解：由三视图可知，该几何体为上部为半径为的球，下部为半径为1，高为2的半个圆柱，‎ 球的表面积：4π×（）2=π，半圆柱的底面面积为2××π=π，‎ 半圆柱的侧面积为2×（2+π）=4+2π．‎ 几何体的表面积为：4+4π．‎ 故选：C．‎ ‎【点评】本题考查三视图求几何体的体积，考查计算能力，空间想象能力，三视图复原几何体是解题的关键．‎ ‎　‎ ‎9．（2016秋•湖北期中）已知点P（x，y）满足过点P的直线与圆x2+y2=36相交于A、B两点，则|AB|的最小值为（　　）‎ A．8 B． C． D．10‎ ‎【考点】简单线性规划．‎ ‎【专题】综合题；转化思想；演绎法；不等式的解法及应用．‎ ‎【分析】不等式对应的平面区域为三角形CDE，C（3，3），D（2，2），E（2，4），利用直线与圆的位置关系，确定点P的位置，进行即可即可．‎ ‎【解答】解：不等式对应的平面区域为三角形CDE，C（3，3），D（2，2），E（2，4）‎ 过点P的直线l与圆x2+y2=36相交于A、B两点，要使|AB|最小，则圆心到过P的直线的距离最大，‎ 当点P在E处时，满足条件，此时OE⊥AB，‎ 此时|OE|==2，‎ ‎∴|AB|=2|BE|=2=8，‎ 故选A．‎ ‎【点评】本题主要考查直线与圆的位置关系的应用，利用直线和圆相交，根据弦长公式确定点P的位置是解决本题的关键，综合性较强．‎ ‎　‎ ‎10．（2016秋•湖北期中）已知一组数据3，4，5，a，b的平均数是4，中位数是m，从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，那么3，4，5，a，b这组数据的方差为（　　）‎ A． B．2 C． D．‎ ‎【考点】极差、方差与标准差．‎ ‎【专题】计算题；方程思想；定义法；概率与统计．‎ ‎【分析】由已知得a=4，b=4，m=4，由此能求出3，4，5，a，b这组数据的方差．‎ ‎【解答】解：∵一组数据3，4，5，a，b的平均数是4，中位数是m，‎ 从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，‎ ‎∴，‎ 解得a=4，b=4，m=4，‎ ‎∴3，4，5，a，b这组数据的方差为：‎ S2=[（3﹣4）2+（4﹣4）2+（5﹣4）2+（4﹣4）2+（4﹣4）2]=．‎ 故选：D．‎ ‎【点评】本题考查方差的求法，是基础题，解题时要认真审题，注意平均数、中位数、概率、方差的性质的合理运用．‎ ‎　‎ ‎11．（2016秋•湖北期中）执行如图所示的程序框图，若输出的S=，判断框内填入的条件可以是（　　）‎ A．n＜10 B．n≤10 C．n≤1024 D．n＜1024‎ ‎【考点】程序框图．‎ ‎【专题】计算题；转化思想；定义法；算法和程序框图．‎ ‎【分析】分析程序框图的运行过程，得出程序输出的算式S的表达式，列出方程求出n的值，即可得出结论．‎ ‎【解答】解：本程序的功能是计算S=+++…+==1﹣，‎ ‎∵S+=，‎ ‎∴S=，‎ ‎∴1﹣=，‎ ‎∴=，‎ ‎∴k=10，即运行了10次，‎ 故可判断框内可填入的条件n≤210=1024，‎ 故选：C ‎【点评】本题主要考查程序框图的识别和判断，等比数列的求和公式，属于基础题．‎ ‎　‎ ‎12．（2016秋•湖北期中）钝角△OAB三边的比为2：2：（﹣），O为坐标原点，A（2，2）、B（a，a），则a的值为（　　）‎ A．2 B． C．2或 D．+‎ ‎【考点】余弦定理．‎ ‎【专题】综合题；分类讨论；综合法；解三角形．‎ ‎【分析】由题意画出图象，由图和题意分两种情况，分别根据余弦定理求出内角的余弦值，由内角的范围和特殊角的三角函数值求出角的大小，由正弦定理求出边OA的值，由点A的坐标求出a的值．‎ ‎【解答】解：由题意画出图象：‎ ‎（1）当OA：0B：AB=2：2：（﹣）时，‎ 则cos∠OBA=‎ ‎==，‎ 因为∠OBA是内角，则∠OBA=120°，‎ cos∠OAB=‎ ‎===，‎ 因为∠OAB是内角，则∠OAB=45°，‎ 在△OAB中，由正弦定理得，‎ 则OB===，‎ 因B（a，a），则a=，解得a=，‎ ‎（2）当OB：0A：AB=2：2：（﹣）时，‎ 则cos∠OAB=‎ ‎==，‎ 因为∠OAB是内角，则∠OAB=120°，‎ cos∠OBA=‎ ‎===，‎ 因为∠OBA是内角，则∠OBA=45°，‎ 在△OAB中，由正弦定理得，‎ 则OB===2，‎ 因B（a，a），则a=2，解得a=2，‎ 综上可得，a的值是或2‎ 故选C．‎ ‎【点评】本题考查了正弦、余弦定理的综合应用，注意内角的范围，考查分类讨论思想，化简、计算能力．‎ ‎　‎ 二、填空题 ‎13．（2016秋•湖北期中）直线2x+y﹣2=0被圆x2+y2=5截得的弦长为　　．‎ ‎【考点】直线与圆的位置关系．‎ ‎【专题】计算题；方程思想；演绎法；直线与圆．‎ ‎【分析】求出圆心到直线的距离，利用半径、半弦长，弦心距满足勾股定理，求出半弦长，即可求出结果．‎ ‎【解答】解：由题意，弦心距为：=；半径为：，半弦长为：，弦长=．‎ 故答案为：．‎ ‎【点评】本题是基础题，考查直线与圆的位置关系，弦长的求法，考查计算能力．‎ ‎　‎ ‎14．（2016秋•湖北期中）已知θ服从上的均匀分布，则2|sinθ|＜成立的概率为　　．‎ ‎【考点】几何概型．‎ ‎【专题】计算题；转化思想；数学模型法；概率与统计．‎ ‎【分析】由θ服从上的均匀分布，在此范围下满足2|sinθ|＜的θ∈[]，利用几何概型能求出概率．‎ ‎【解答】解：θ服从上的均匀分布，区间长度为π，‎ 在此范围下满足2|sinθ|＜的θ∈[]，区间长度为，‎ 由几何概型得到所求概率为；‎ 故答案为：．‎ ‎【点评】本题考查了几何概型的概率求法；关键是明确利用区间长度的比求概率．‎ ‎　‎ ‎15．（2016秋•湖北期中）已知四面体P﹣ABC各面都是直角三角形，且最长棱长PC=2，则此四面体外接球的表面积为　12π　．‎ ‎【考点】球的体积和表面积；球内接多面体．‎ ‎【专题】综合题；方程思想；演绎法；空间位置关系与距离．‎ ‎【分析】根据已知可得三棱锥的外接球的直径为2，进而求出球半径，代入球的表面积公式，可得答案．‎ ‎【解答】解：若三棱锥P﹣ABC的最长的棱PA=2，且各面均为直角三角形，‎ 将此三棱锥的外接球的直径为2，‎ 故此三棱锥的外接球的半径为，‎ 故此三棱锥的外接球的表面积S=4π•3=12π，‎ 故答案为：12π．‎ ‎【点评】本题考查的知识点是球的体积与表面积，根据已知得到球的半径，是解答的关键．‎ ‎　‎ ‎16．（2016秋•湖北期中）记Min{a，b}为a、b两数中的最小值，当正数x，y变化时，令t=Min{4x+y，}，则t的最大值为　2　．‎ ‎【考点】函数的最值及其几何意义；不等式比较大小．‎ ‎【专题】分类讨论；分析法；函数的性质及应用；不等式的解法及应用．‎ ‎【分析】利用重要不等式进行放缩，再分类讨论．‎ ‎【解答】解：∵，‎ ‎∴当时有4x+y≤2；‎ 当时，有，‎ ‎∴t≤2，‎ 故答案：2．‎ ‎【点评】本题考查了简单的放缩法，分类讨论法，一种常见的不等关系处理方法，属于中档题．‎ ‎　‎ 三、解答题 ‎17．（12分）（2016秋•湖北期中）某小学对五年级的学生进行体质测试，已测得五年级一班30名学生的跳远成绩（单位：cm），用茎叶图统计如图，男生成绩在175cm以上（包括175cm）定义为合格，成绩在175cm以下（不含175cm）定义为“不合格”；女生成绩在165以上（包括165cm）定义为“合格”，成绩在165cm以下（不含165cm）定义为“不合格”．‎ ‎（1）求男生跳远成绩的中位数．‎ ‎（2）根据男女生的不同，用分层抽样的方法从该班学生中抽取1个容量为5的样本，求抽取的5人中女生的人数．‎ ‎（3）以此作为样本，估计该校五年级学生体质的合格率．‎ ‎【考点】古典概型及其概率计算公式；茎叶图．‎ ‎【专题】计算题；方程思想；定义法；概率与统计．‎ ‎【分析】（1）男生跳远成绩数据为偶数个，能求出中位数．‎ ‎（2）女生总人数为18人，所占比例为，由此能求出女生应抽取的人数．‎ ‎（3）由茎叶图求出样本的合格率，由此能求出该校五年级学生体质的合格率．‎ ‎【解答】解：（1）男生跳远成绩数据为偶数个，‎ ‎∴中位数为（cm）．…（4分）‎ ‎（2）女生总人数为18人，所占比例为，‎ ‎∴女生应抽取的人数为人．…（8分）‎ ‎（3）由茎叶图可知，‎ 样本中男生有8人合格，女生有10人合格．‎ 样本的合格率为=60%．‎ ‎∴该校五年级学生体质的合格率估计为60%．…（12分）‎ ‎【点评】本题考查中位数、频数、合格率的求法，是基础题，解题时要认真审题，注意茎叶图性质的合理运用．‎ ‎　‎ ‎18．（12分）（2016秋•湖北期中）已知函数f（x）=在（﹣1，+∞）是增函数．‎ ‎（1）当b=1时，求a的取值范围．‎ ‎（2）若g（x）=f（x）﹣1008没有零点，f（1）=0，求f（﹣3）的值．‎ ‎【考点】根的存在性及根的个数判断；函数单调性的判断与证明；函数的零点与方程根的关系．‎ ‎【专题】计算题；函数思想；转化思想；解题方法；函数的性质及应用．‎ ‎【分析】（1）利用分离常数法，通过函数的单调性求解即可．‎ ‎（2）求出函数的对称点的坐标，推出关系式，然后求解a，利用f（x）+f（﹣2﹣x）=2a求解即可．‎ ‎【解答】解：（1）b=1时 …（3分）‎ ‎∵f（x）在（﹣1，+∞）上是增函数，‎ ‎∴1﹣a＜0即a＞1．‎ 所求a的范围为（1，+∞）．…（6分）‎ ‎（2），∴f（x）关于点（﹣1，a）对称．‎ 即f（x）+f（﹣2﹣x）=2a…（8分）‎ ‎∵g（x）=f（x）﹣1008没有零点，‎ ‎∴a=1008…（10分）‎ ‎∵f（1）=0又f（1）+f（﹣3）=2×1008=2016‎ ‎∴f（﹣3）=2016…（12分）‎ ‎【点评】本题考查函数的零点个数，函数的单调性，对称性的应用，考查计算能力．另：本题也可以先求a、b再求f（﹣3）．‎ ‎　‎ ‎19．（12分）（2016秋•湖北期中）在数列{an}中，a1=1an+1=，n∈N*．‎ ‎（1）求证数列为等比数列．‎ ‎（2）求数列{an}的前n项和Sn．‎ ‎【考点】数列递推式．‎ ‎【专题】综合题；函数思想；数学模型法；等差数列与等比数列．‎ ‎【分析】（1）直接把已知数列递推式变形可得，即是首项为1，公比为2的等比数列；‎ ‎（2）由（1）求出数列{an}的通项公式，再由错位相减法求数列{an}的前n项和Sn．‎ ‎【解答】（1）证明：由，得，‎ 又，‎ ‎∴是首项为1，公比为2的等比数列；‎ ‎（2）解：由（1）知，是首项为1，公比为2的等比数列，‎ ‎∴，则，‎ 则，‎ ‎…+（n﹣1）•2n﹣1+n•2n，‎ 两式作差得：﹣Sn=1+2+22+2n﹣1﹣n•2n=2n﹣1﹣n•2n=（1﹣n）•2n﹣1，‎ ‎∴．‎ ‎【点评】本题考查数列递推式，考查了等比关系的确定，训练了错位相减法求数列的前n项和，是中档题．‎ ‎　‎ ‎20．（12分）（2016秋•湖北期中）在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，∠APD=90°，PA=PD=AB=a，ABCD是矩形，E是PD的中点．‎ ‎（1）求证：PB⊥AC．‎ ‎（2）求二面角E﹣AC﹣D的正切值．‎ ‎【考点】二面角的平面角及求法；直线与平面垂直的性质．‎ ‎【专题】证明题；转化思想；综合法；空间位置关系与距离；空间角．‎ ‎【分析】（1）设AD中点为F，连接BF、PF，推导出△ABC∽△FAB，从而AC⊥BF，推导出PF⊥AC，由此能证明AC⊥PB．‎ ‎（2）过E作EH∥PF，EH交AD于H，过H作HO⊥AC，交AC于O，连接EO，则∠EOH为二面角E﹣AC﹣D的平面角，由此能求出二面角E﹣AC﹣D的正切值．‎ ‎【解答】证明：（1）设AD中点为F连接BF、PF．‎ ‎∵PA=PD=AB=a，∴，‎ ‎∴．‎ ‎∴△ABC∽△FAB，∴AC⊥BF，…（4分）‎ 又∵PF⊥AD，又∵平面PAD⊥平面ABCD．‎ 平面PAD∩平面ABCD=AD，‎ ‎∴PF⊥面ABC，∴PF⊥AC，‎ ‎∴AC⊥平面PBF，AC⊥PB．…（6分）‎ 解：（2）过E作EH∥PF，EH交AD于H，‎ 过H作HO⊥AC，交AC于O，连接EO．‎ 由（1）知EH⊥面ACD，HO⊥AC，‎ ‎∴∠EOH为二面角E﹣AC﹣D的平面角…（8分）‎ ‎．‎ ‎．‎ ‎∴．‎ ‎∴二面角E﹣AC﹣D的正切值为．…（12分）‎ ‎【点评】本题考查线线垂直的证明，考查二面角的正切值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．‎ ‎　‎ ‎21．（12分）（2016秋•湖北期中）已知圆C1：（x+2）2+（y﹣1）2=4与圆C2：（x﹣3）2+（y﹣4）2=4，过点P（﹣1，5）作两条互相垂直的直线l1：y=k（x+1）+5，l2：y=﹣（x+1）+5．‎ ‎（1）若k=2时，设l1与圆C1交于A、B两点，求经过A、B两点面积最小的圆的方程．‎ ‎（2）若l1与圆C1相交，求证：l2与圆C2相交，且l1被圆C1截得的弦长与l2被圆C2截得的弦长相等．‎ ‎（3）是否存在点Q，过Q的无数多对斜率之积为1的直线l3，l4，l3被圆C1截得的弦长与l4被圆C2截得的弦长相等．若存在求Q的坐标，若不存在，说明理由．‎ ‎【考点】直线与圆的位置关系．‎ ‎【专题】综合题；转化思想；演绎法；直线与圆．‎ ‎【分析】（1）经过A、B两点面积最小的圆应是以AB为直径的圆；‎ ‎（2）证明l2与圆C2相交，利用两圆的半径相等，而两弦心距相等，可得所截得的弦长相等；‎ ‎（3）由d3=d4得|1﹣b+m（a+2）|=|a﹣3+m（4﹣b）|∴1﹣b+m（a+2）=a﹣3+m（4﹣b）（1）或1﹣b+m（a+2）=3﹣a+m（b﹣4）（2），（1）（2）对于无数多个m的值都成立．（3）或（4），（3）（4）都无解，即可得出结论．‎ ‎【解答】解：（1）当k=2时，l1的方程为y=2x+7‎ 联立方程组，整理得5x2+28x+36=0‎ 设A、B为A（x1，y1），B（x2，y2）∴，，，，‎ 经过A、B两点面积最小的圆应是以AB为直径的圆，‎ 圆的方程为（x﹣x1）（x﹣x2）+（y﹣y1）（y﹣y2）=0．‎ 即x2+y2﹣（x1+x2）x﹣（y1+y2）y+x1x2+y1y2=0‎ 所求圆的方程：…（4分）‎ ‎（2）设圆C1的圆心到l1的距离为d1，圆C2的圆心到l2的距离为d2，则，‎ ‎∴l2与圆C2相交，‎ ‎∵两圆的半径相等，而两弦心距相等，‎ ‎∴所截得的弦长相等．‎ ‎（3）设Q（a，b）ℓ3的方程为y=m（x﹣a）+b．l4的方程为，‎ 依题意圆C1的圆心到l3的距离为，‎ 由d3=d4得|1﹣b+m（a+2）|=|a﹣3+m（4﹣b）|∴1﹣b+m（a+2）=a﹣3+m（4﹣b）（1）‎ 或1﹣b+m（a+2）=3﹣a+m（b﹣4）（2）‎ ‎（1）（2）对于无数多个m的值都成立∴（3）或（4）‎ ‎（3）（4）都无解∴Q不存在…（12分）‎ ‎【点评】本题考查圆的方程，考查直线与圆的位置关系，考查学生分析解决问题的能力，难度大．‎ ‎　‎ ‎22．（10分）（2016秋•湖北期中）在△ABC中，三个内角A，B，C所对的边分别为a，b，c，已知函数f（x）=sin（3x+B）+cos（3x+B）是偶函数，且b=f（）．‎ ‎（1）求b．‎ ‎（2）若a=，求角C．‎ ‎【考点】正弦定理．‎ ‎【专题】计算题；转化思想；综合法；解三角形．‎ ‎【分析】（1）利用两角和的正弦函数公式化简函数解析式可得f（x）=，由题意可得 ‎，结合B范围可求B，求得解析式，即可得解b=f（）的值．‎ ‎（2）由已知及正弦定理得，结合大边对大角及A的范围可求A，利用三角形内角和定理即可得解C的值．‎ ‎【解答】（本题满分为10分）‎ 解：（1）f（x）=sin（3x+B）+cos（3x+B）=，‎ ‎∵f（x）是偶函数，‎ ‎∴…（2分）‎ ‎∵B∈（0，π），‎ ‎∴…（4分）‎ ‎∴，‎ ‎∴．…（6分）‎ ‎（2）∵，由正弦定理得：，…（8分）‎ ‎∵a＜b，‎ ‎∴，‎ ‎∴从而．…（10分）‎ ‎【点评】本题主要考查了两角和的正弦函数公式，正弦定理，大边对大角，三角形内角和定理在解三角形中的应用，考查了转化思想，属于基础题．‎