高中数学（人教A版）必修3能力强化提升及单元测试2-2-2 4页

‎2.2.2　用样本的数字特征估计 总体的数字特征 双基达标　(限时20分钟) ‎1．下面是高一(18)班十位同学的数学测试成绩：82,91,73,84,98,99,101,118,98,110，则该组数据的中位数是 (　　)．‎ A．98 B．99 C．98.5 D．97.5‎ 解析　将这组数据按从小到大排列为73,82,84,91,98,98,99,101,110,118，则最中间的两个数为98,98，故中位数是(98＋98)＝98.‎ 答案　A ‎2．某学习小组在一次数学测验中，得100分的有1人，95分的有1人，90分的有2人，85分的有4人，80分和75分的各有1人，则该小组成绩的平均数、众数、中位数分别是(　　)．‎ A．85,85,85 B．87,85,86‎ C．87,85,85 D．87,85,90‎ 解析　从小到大列出所有数学成绩：75,80,85,85,85,85,90,90,95,100，观察知众数和中位数均为85，计算得平均数为87.‎ 答案　C ‎3．为了让人们感受丢弃塑料袋对环境造成的影响，某班环保小组的六名同学记录了自己家中一周内丢弃的塑料袋的数量，结果如下(单位：个)：33,25,28,26,25,31.如果该班有45名学生，那么根据提供的数据估计本周全班同学各家总共丢弃塑料袋的数量约为(　　)‎ A．900个 B．1 080个 ‎ C．1 260个 D．1 800个 解析　(33＋25＋28＋26＋25＋31)×45＝1 260(个)．故选C.‎ 答案　C ‎4．已知样本9,10,11，x，y的平均数是10，标准差是，则xy＝________.‎ 解析　由平均数得9＋10＋11＋x＋y＝50，‎ ‎∴x＋y＝20，又由(9－10)2＋(10－10)2＋(11－10)2＋(x－10)2＋(y－10)2＝()2×5＝10，‎ 得x2＋y2－20(x＋y)＝－192，(x＋y)2－2xy－20(x＋y)＝－192，xy＝96.‎ 答案　96‎ ‎5．若40个数据的平方和是56，平均数是，则这组数据的方差是________，标准差是________．‎ 解析　设这40个数据为xi(i＝1,2，…，40)，平均数为.‎ 则s2＝×[(x1－)2＋(x2－)2＋…＋(x40－)2]‎ ‎＝[x12＋x22＋…＋x402＋402－2(x1＋x2＋…＋x40)]‎ ‎＝ ‎＝× ‎＝0.9.‎ ‎∴s＝＝ ＝.‎ 答案　0.9　 ‎6．在一次歌手大奖赛中，8位评委现场给每位歌手打分，然后去掉一个最高分和一个最低分，其余分数的平均数作为该歌手的成绩，已知8位评委给某位歌手的打分是：9.2　9.5　9.4　9.6　9.8　9.5　8.1　9.5‎ 比较这8位评委的实际平均分和该歌手的成绩，有何体会？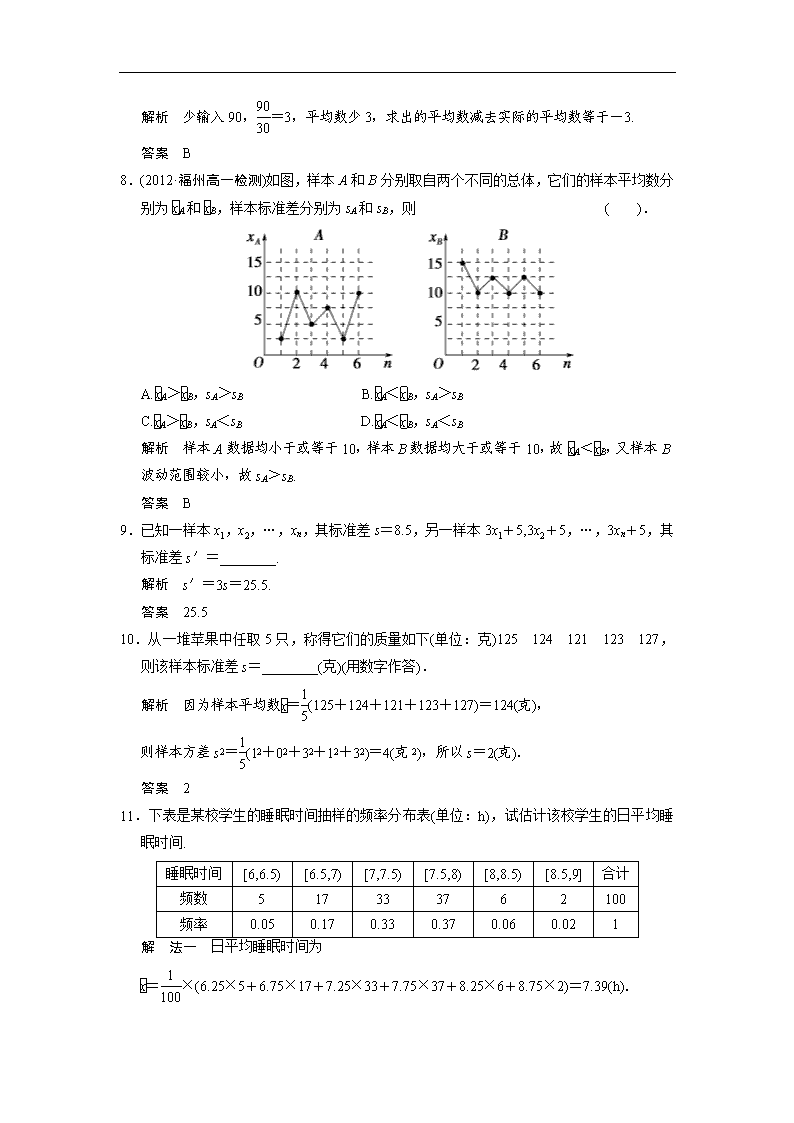‎ 解　实际平均分为＝(9.2＋9.5＋9.4＋9.6＋9.8＋9.5＋8.1＋9.5)＝9.325.‎ 该歌手的得分为′＝(9.2＋9.5＋9.4＋9.6＋9.5＋9.5)＝9.45.‎ 因为9.5在这组数据中出现3次，出现次数最多，故打分的众数是9.5，将这组数据按从小到大的顺序排列，则最中间的两个数是9.5，故中位数是9.5.由此可见，去掉一个最高分，去掉一个最低分后能比较恰当地反映该歌手的实际成绩．‎ 综合提高　(限时25分钟) ‎7．某同学使用计算器求30个数据的平均数时，错将其中一个数据105输入为15，那么由此求出的平均数与实际平均数的差是 (　　)．‎ A．3.5 B．－3 C．3 D．－0.5‎ 解析　少输入90，＝3，平均数少3，求出的平均数减去实际的平均数等于－3.‎ 答案　B ‎8．(2012·福州高一检测)如图，样本A和B分别取自两个不同的总体，它们的样本平均数分别为A和B，样本标准差分别为sA和sB，则 (　　)．‎ A.A＞B，sA＞sB B.A＜B，sA＞sB C.A＞B，sA＜sB D.A＜B，sA＜sB 解析　样本A数据均小于或等于10，样本B数据均大于或等于10，故A＜B，又样本B波动范围较小，故sA＞sB.‎ 答案　B ‎9．已知一样本x1，x2，…，xn，其标准差s＝8.5，另一样本3x1＋5,3x2＋5，…，3xn＋5，其标准差s′＝________.‎ 解析　s′＝3s＝25.5.‎ 答案　25.5‎ ‎10．从一堆苹果中任取5只，称得它们的质量如下(单位：克)125　124　121　123　127，则该样本标准差s＝________(克)(用数字作答)．‎ 解析　因为样本平均数＝(125＋124＋121＋123＋127)＝124(克)，‎ 则样本方差s2＝(12＋02＋32＋12＋32)＝4(克2)，所以s＝2(克)．‎ 答案　2‎ ‎11．下表是某校学生的睡眠时间抽样的频率分布表(单位：h)，试估计该校学生的日平均睡眠时间.‎ 睡眠时间 ‎[6,6.5)‎ ‎[6.5,7)‎ ‎[7,7.5)‎ ‎[7.5,8)‎ ‎[8,8.5)‎ ‎[8.5,9]‎ 合计 频数 ‎5‎ ‎17‎ ‎33‎ ‎37‎ ‎6‎ ‎2‎ ‎100‎ 频率 ‎0.05‎ ‎0.17‎ ‎0.33‎ ‎0.37‎ ‎0.06‎ ‎0.02‎ ‎1‎ 解　法一　日平均睡眠时间为 ＝×(6.25×5＋6.75×17＋7.25×33＋7.75×37＋8.25×6＋8.75×2)＝7.39(h)．‎ 法二　求组中值与对应频率之积的和 ＝6.25×0.05＋6.75×0.17＋7.25×0.33＋7.75×0.37＋8.25×0.06＋8.75×0.02＝7.39(h)．‎ 所以，估计该校学生的日平均睡眠时间约为7.39 h.‎ ‎12．(创新拓展)随机抽取某中学甲、乙两班各10名同学，测量他们的身高(单位：cm)，获得身高数据的茎叶图如图．‎ ‎(1)根据茎叶图判断哪个班的平均身高较高；‎ ‎(2)计算甲班的样本方差．‎ 解　(1)乙班的平均身高较高．(可由茎叶图判断或计算得出)‎ ‎(2)因为甲班的平均身高为＝i＝170(cm)，所以甲班的样本方差s2＝(xi－)2＝(2×122＋2×92＋2×22＋12＋72＋82＋02)＝57.2.‎