高中数学必修5综合测试题及答案 7页

必修5综合测试题（2010.11）‎ ‎ 班级 姓名 ‎ 一、选择题 ‎1. 数列1，3，6，10，…的一个通项公式是（ ）‎ A. an=n2-(n-1) B . an=n2‎-1 C. an= D. an=‎ ‎2. 是a,b,c成等比数列的（ ）‎ A、充分非必要条件 B、必要非充分条件 C、充要条件 D、既不充分也非必要条件 ‎3．已知等差数列{an}的公差d≠0,若a5、a9、a15成等比数列,那么公比为 ( ) ‎ A． B． C． D．‎ ‎4. 等差数列{an}共有2n+1项，其中奇数项之和为4，偶数项之和为3，则n的值是( )‎ A.3 B‎.5 ‎‎ C.7 D.9‎ ‎5．△ABC 中，，则△ABC一定是( )‎ A．等腰三角形 B．直角三角形 ‎ C．等腰直角三角形 D．等边三角形 ‎6．已知△ABC中，a＝4，b＝4，∠A＝30°，则∠B等于( )‎ A．30° B．30°或150° C．60° D．60°或120°‎ ‎7. 在△ABC中，∠A=60°,a=,b=4,满足条件的△ABC( )‎ ‎(A)无解 (B)有解 (C)有两解 (D)不能确定 ‎8．若，则下列不等式中，正确的不等式有 ( ) ‎ ‎① ② ③ ④‎ A.1个 B.2个 C.3个 D.4个 ‎9．下列不等式中，对任意x∈R都成立的是 ( ) ‎ A． B．x2+1>2x ‎ ‎ C．lg(x2+1)≥lg2x D．≤1‎ ‎10. 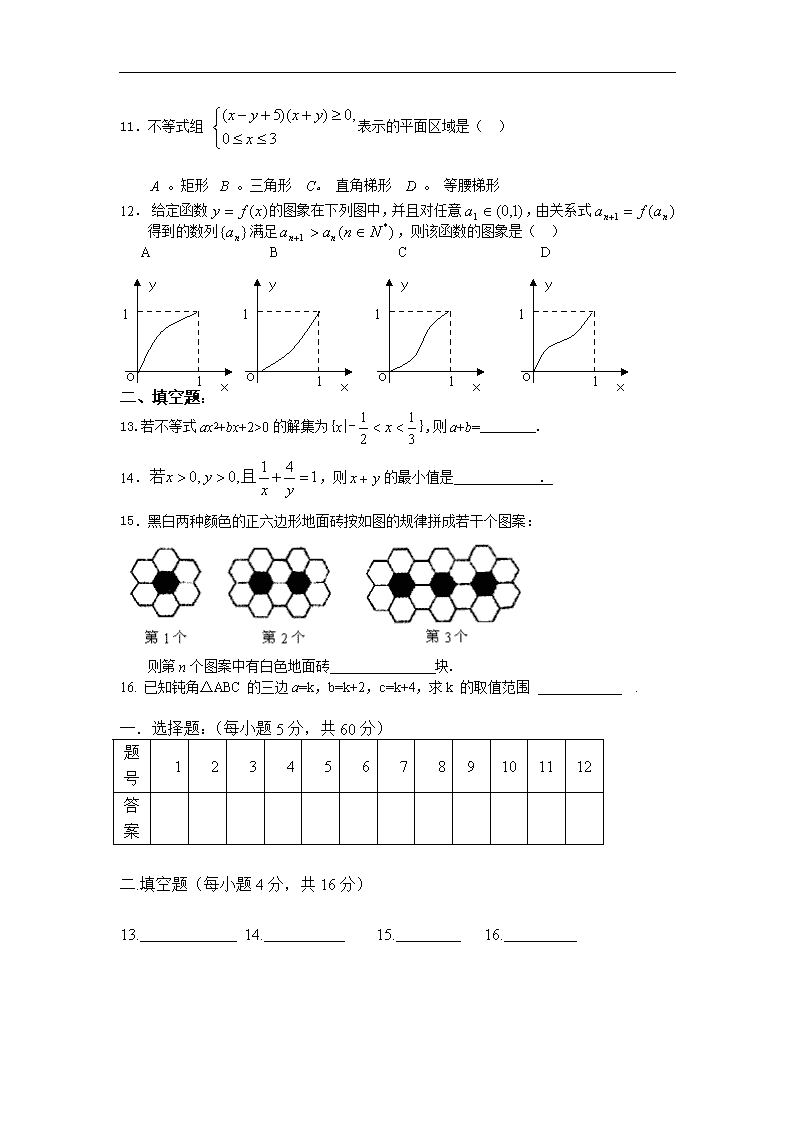下列不等式的解集是空集的是( )‎ A.x2-x+1>0 B.-2x2+x+1>‎0 ‎‎ C.2x-x2>5 D.x2+x>2‎ ‎11．不等式组 表示的平面区域是（ ） ‎ ‎ A 。矩形 B 。三角形 C。 直角梯形 D 。 等腰梯形 ‎12． 给定函数的图象在下列图中，并且对任意，由关系式得到的数列满足，则该函数的图象是（ ）‎ A B C D ｏ ‎1‎ ‎1‎ ｘ ｙ ｏ ‎1‎ ‎1‎ ｘ ｙ ｏ ‎1‎ ‎1‎ ｘ ｙ ｏ ‎1‎ ‎1‎ ｘ ｙ 二、填空题：‎ ‎13.若不等式ax2+bx+2>0的解集为{x|-},则a+b=________.‎ ‎14．，则的最小值是 ．‎ ‎15．黑白两种颜色的正六边形地面砖按如图的规律拼成若干个图案：‎ 则第n个图案中有白色地面砖 块.‎ ‎16. 已知钝角△ABC的三边a=k，b=k+2，c=k+4，求k 的取值范围 . ‎ 一．选择题：（每小题5分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 二.填空题（每小题4分，共16分）‎ ‎13. 14. 15. 16. ‎ 三、解答题：‎ ‎17．已知、、为的三内角，且其对边分别为、、，若．‎ ‎（Ⅰ）求； （Ⅱ）若，求的面积．‎ ‎18．设数列的前项n和为，若对于任意的正整数n都有.‎ ‎（1）设，求证：数列是等比数列，并求出的通项公式。‎ ‎（2）求数列的前n项和. ‎ ‎19．某工厂家具车间造A、B型两类桌子，每张桌子需木工和漆工两道工序完成已知木工做一张A、B型桌子分别需要1小时和2小时，漆工油漆一张A、B型桌子分别需要3小时和1小时；又知木工、漆工每天工作分别不得超过8小时和9小时，而工厂造一张A、B型桌子分别获利润2千元和3千元，试问工厂每天应生产A、B型桌子各多少张，才能获得利润最大？‎ ‎20．在平面直角坐标系中，设矩形OPQR的顶点按逆时针顺序依次为O(0,0),P(1,t) Q(1－2t,2+t),R(－2t,2)其中t(0,+∞),‎ ‎（1）求矩形OPQR在第一象限部分的面积S(t)； ‎ ‎（2）求S(t)的最小值． ‎ 新课标第一网 ‎21、已知数列{}的前n项和，求数列{||}的前n项和. ‎ ‎22．设数列{an}的前n项为Sn，点均在函数y = 3x－2的图象上.‎ ‎ （1）求数列{an}的通项公式。‎ ‎ （2）设，Tn为数列{bn}的前n项和，求使得对所有都成立的最小正整数m.‎ 答案：1---12 CBCAA, DABDC, DA ‎13.-14, 14.9 15. 4n+2 16. (2,6)‎ ‎17. 解：（Ⅰ）‎ ‎ ‎ 又，‎ ‎ ， ． ‎ ‎（Ⅱ）由余弦定理 得 ‎ 即：， ‎ ‎．‎ ‎18．解：（1）对于任意的正整数都成立， ‎ 两式相减，得 ‎∴， 即 ‎，即对一切正整数都成立。‎ ‎∴数列是等比数列。‎ 由已知得 即 ‎∴首项，公比，。。‎ ‎ ‎ ‎19.. 解：设每天生产A型桌子x张，B型桌子y张，则 目标函数为：z=2x+3y 作出可行域： ‎ 把直线：2x+3y=0向右上方平移至的位置时，直 线经过可行域上的点M，且与原点距离最大，此时z=2x+3y取最大值 解方程得M的坐标为（2，3）.‎ 答：每天应生产A型桌子2张，B型桌子3张才能获得最大利润 ‎20． （14分）[解析]：，‎ ‎（1）当RQ与y轴交与点S，即设S（0,m），‎ ‎，，‎ ‎ ；‎ 当PQ与y轴交与点S，即设S（0,n），，‎ ‎，.‎ 综上知：S(t)= ．‎ ‎（2）当时，；当时，，这时t=1.‎ 的最小值为1．‎ www.xkb1.com ‎21、 ‎ ‎22．解：（1）∵点在函数y = 3x－2的图象上，‎ ‎ ……………………………………3分 ‎∴a1= s1 =1‎ 当 ‎ ………………………………………… 6分 ‎ （2） …………8分 ‎ ‎ ‎ ‎ ‎ ‎ ‎ 因此，使得成立的m必须且仅需满足，故满足要求的最小整数m为10.……………………12分