2017届高考文科数学（全国通用）二轮文档讲义：第3编八大提分笔记-8推理与证明、复数、算法 5页

八、推理与证明、复数、算法 ‎1推理方法 ‎(1)合情推理 合情推理是根据已有的事实和正确的结论(包括定义、公理、定理等)，实验和实践的结果，以及个人的经验和直觉等推测某些结果的推理过程，归纳和类比是合情推理常见的方法，在解决问题的过程中，合情推理具有猜测和发现结论、探索和提供思路的作用，有利于创新意识的培养．‎ ‎①类比推理是用一类事物的性质去推测另一类事物的性质，得出一个明确的命题(猜想)，类比的结论不一定正确．‎ ‎②归纳推理是由部分推知整体的一种合情推理，和类比推理一样，“合乎情理”是其主要特征，即我们作出的归纳首先要适合“部分”．‎ ‎(2)演绎推理 演绎推理是指如果推理是从一般性的原理出发，推出某个特殊情况下的结论，我们把这种推理称为演绎推理，演绎推理的一般模式是“三段论”，包括：①大前提；②小前提；③结论．‎ ‎2证明方法 ‎(1)直接证明 ‎①综合法 一般地，利用已知条件和某些数学定义、定理、公理等，经过一系列的推理论证，最后推导出所要证明的结论成立，这种证明方法叫综合法．综合法又叫顺推法或由因导果法．‎ ‎②分析法 一般地，从要证明的结论出发，逐步寻求使它成立的充分条件，直至最后，把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、定理、公理等)，这种证明方法叫分析法．分析法又叫逆推法或执果索因法．‎ ‎(2)间接证明——反证法 一般地，假设原命题不成立，经过正确的推理，最后得出矛盾，因此说明假设错误，从而证明原命题成立，这种证明方法叫反证法．‎ ‎3复数的概念 对于复数a＋bi(a，b∈R)，a叫做实部，b叫做虚部；当且仅当b＝0时，复数a＋bi(a，b∈R)是实数a；当b≠0时，复数a＋bi叫做虚数；当a＝0且b≠0时，复数a＋bi叫做纯虚数．‎ ‎4复数的运算法则与实数运算法则相同，主要是除法法则的运用，另外复数中的几个常用结论应记熟：‎ ‎(1)(1±i)2＝±2i；(2)＝i；＝－i；(3)i4n＝1；i4n＋1＝i；i4n＋2＝－1；i4n＋3＝－i；i4n＋i4n＋1＋i4n＋2＋i4n＋3＝0；‎ ‎(4)设ω＝－±i，则ω0＝1；ω2＝；ω3＝1；1＋ω＋ω2＝0.‎ ‎5解决程序框图问题时，一定要仔细分析程序框图的实际意义是什么，也就是这个程序框图要解决什么问题，从什么时候开始、中间按照什么规律进行、在什么条件下结束．这是分析程序框图的一个基本思路．‎ 复数概念不清致误 　　[2016·广州综合测试]已知复数z＝，其中i为虚数单位，则复数z的共轭复数所对应的点在(　　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎[错解]　z＝＝＝1＋2i，故在复平面内对应的点为(－1，－2)，选A.‎ ‎[错因分析]　z的共轭复数＝1－2i，对应点为(1，－2)．‎ ‎[正解]　z＝＝＝1＋2i，所以z的共轭复数为1－2i，对应复平面内的点为(1，－2)，故选D.‎ ‎[答案]　D ‎[防范措施]　熟练掌握复数的相关概念及运算法则是解决此类问题的关键.‎ 补救训练1　设复数z1＝1－i，z2＝a＋2i，若的虚部是实部的2倍，则实数a的值为(　　)‎ A．6 B．－6‎ C．2 D．－2‎ 答案　A 解析　＝＝＝，故该复数的实部是，虚部是.‎ 由题意，知＝2×.‎ 解得a＝6.故选A.‎ 循环结构判断不准致误 　　[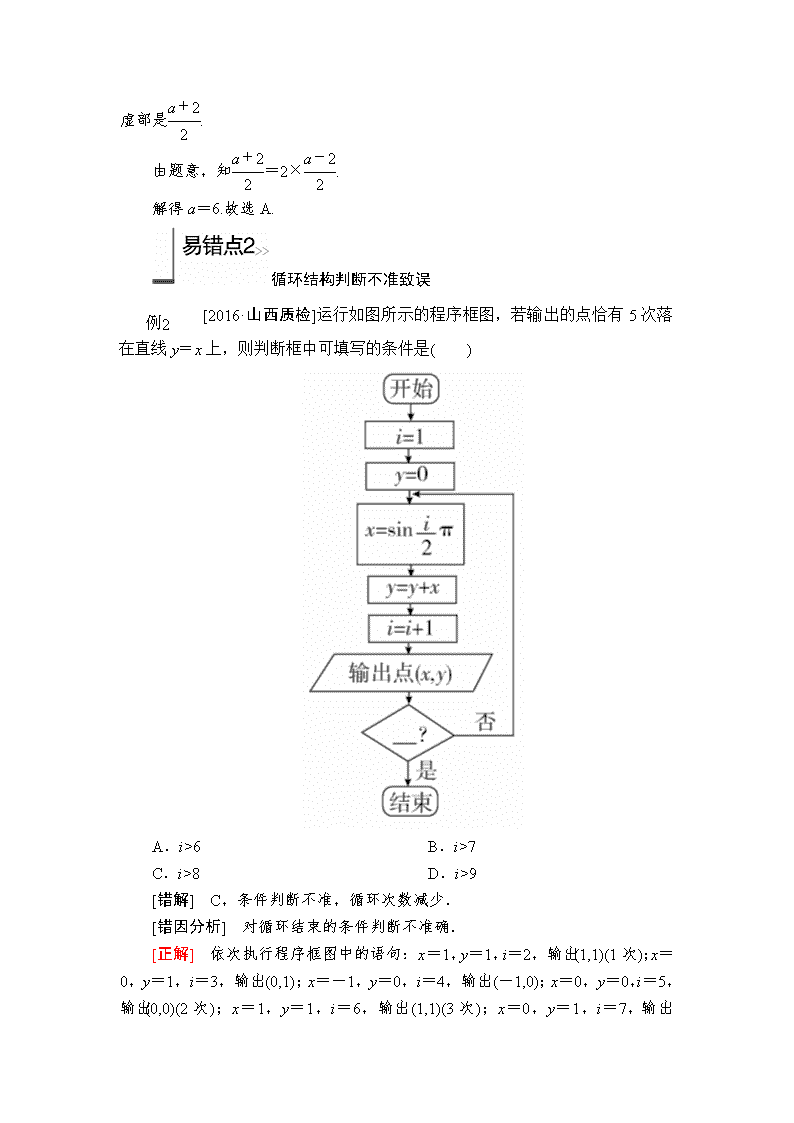2016·山西质检]运行如图所示的程序框图，若输出的点恰有5次落在直线y＝x上，则判断框中可填写的条件是(　　)‎ A．i>6 B．i>7‎ C．i>8 D．i>9‎ ‎[错解]　C，条件判断不准，循环次数减少．‎ ‎[错因分析]　对循环结束的条件判断不准确．‎ ‎[正解]　依次执行程序框图中的语句：x＝1，y＝1，i＝2，输出(1,1)(1次)；x＝0，y＝1，i＝3，输出(0,1)；x＝－1，y＝0，i＝4，输出(－1,0)；x＝0，y＝0，i＝5，输出(0,0)(2次)；x＝1，y＝1，i＝6，输出(1,1)(3次)；x＝0，y＝1，i＝7，输出(0,1)；x＝－1，y＝0，i＝8，输出(－1,0)；x＝0，y＝0，i＝9，输出(0,0)(4次)；x＝1，y＝1，i ‎＝10，输出(1,1)(5次)，此时跳出循环，故判断框中可填写的条件是“i>9？”，故选D.‎ ‎[答案]　D ‎[防范措施]　条件结构的程序框图是对判断条件的分类，是逐级进行的，其中不能有遗漏和重复，在解题时要对判断条件仔细辨别，看清条件的函数的对应关系.‎ 补救训练2　[2016·海口调研]执行如图的程序框图，则输出的i＝________.‎ 答案　4‎ 解析　进行第一次循环时，S＝＝20，i＝2，S＝20>1；进行第二次循环时，S＝＝4，i＝3，S＝4>1；进行第三次循环时，S＝＝0.8，i＝4，S＝0.8<1，此时结束循环，输出的i＝4.‎ 归纳不严密致误 　　[2016·湖北七市联考]观察下列等式 ‎1＋2＋3＋…＋n＝n(n＋1)；‎ ‎1＋3＋6＋…＋n(n＋1)＝n(n＋1)(n＋2)；‎ ‎1＋4＋10＋…＋n(n＋1)(n＋2)＝n(n＋1)(n＋2)·(n＋3)；‎ 可以推测，1＋5＋15＋…＋n(n＋1)(n＋2)(n＋3)＝________.‎ ‎[错解]　根据式子的给出规律可知，‎ 等式右侧为n(n＋1)(n＋2)(n＋3)(n＋4)．‎ ‎[错因分析]　右侧的出现规律归纳不准确．‎ ‎[正解]　根据式子中的规律可知，等式右侧为n(n＋1)(n＋2)(n＋3)(n＋4)＝n(n＋1)·(n＋2)(n＋3)(n＋4)．‎ ‎[答案]　n(n＋1)(n＋2)(n＋3)(n＋4)‎ ‎[防范措施]　熟练掌握归纳推理的解题思路：观察——推广——猜测，把握所给式子的结构特征及出现规律.‎ 补救训练3　观察下列等式：13＝12,13＋23＝32,13＋23＋33＝62,13＋23＋33＋43＝102，…，根据上述规律，第n个等式为________．‎ 答案　13＋23＋33＋43＋…＋n3＝2‎ 解析　由题知13＝12；‎ ‎13＋23＝2；‎ ‎13＋23＋33＝2；‎ ‎13＋23＋33＋43＝2；‎ ‎…‎ ‎∴13＋23＋33＋43＋…＋n3＝2.‎