专题03+二次方程根的分布问题-2019年高考数学二轮复习之重难点微专题突破训练 6页

结论1：方程有且只有一个实根在内,等价于,或且,或且。‎ 例：若方程在内恰有一解，则的取值范围为(  )‎ A. B. C. D.‎ ‎【答案】B ‎【掌握练习】‎ ‎1、关于的方程在区间上有唯一实根，则实数的取值范围为（　　）‎ A. B. C.  D.‎ ‎【答案】D ‎【解析】‎ ‎∵方程在区间上有唯一实根，‎ ‎∴，当且仅当时取等号，‎ 所以在区间上实数的取值范围为.‎ ‎2、若方程在区间上有且仅有一根，则实数的取值范围是（　　）‎ A.  B.  C. D.‎ ‎【答案】C ‎【解析】‎ 方程在区间上有且仅有一个根，则，‎ 即，解得.‎ 结论2：‎ 分布情况 两个负根即两根都小于0‎ 两个正根即两根都大于0‎ 一正根一负根即一个根小于0，一个大于0‎ 综合结论（不讨论）‎ 例：一元二次方程的两个根都是正数，则的取值范围是(　　)‎ A.或 B. ‎ C. D. ‎ ‎【答案】A ‎【掌握练习】‎ ‎1、已知二次方程有一正根和一负根，则实数的取值范围是(  )‎ A.或 B. C. 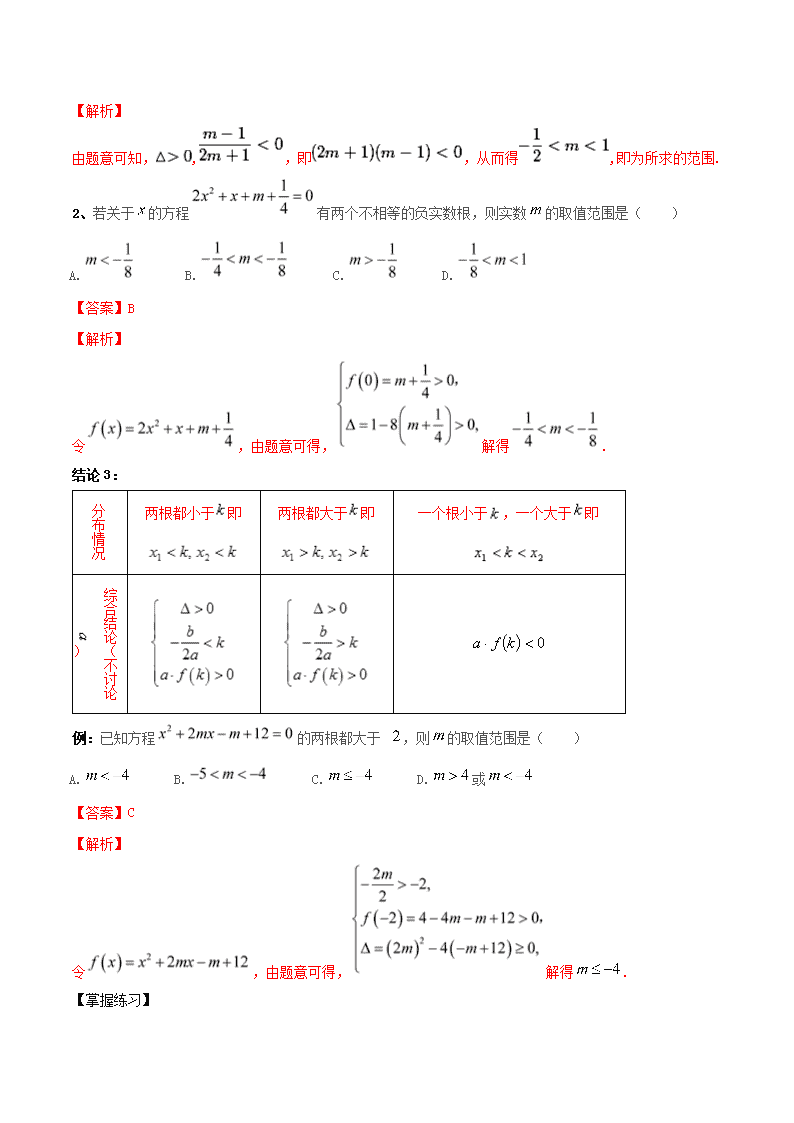D.‎ ‎【答案】C ‎【解析】‎ 由题意可知，,，即，从而得,即为所求的范围.‎ ‎2、若关于的方程有两个不相等的负实数根，则实数的取值范围是（　　）‎ A. B. C. D.‎ ‎【答案】B ‎【解析】‎ 令，由题意可得，解得.‎ 结论3：‎ 分布情况 两根都小于即 两根都大于即 一个根小于，一个大于即 综合结论（不讨论）‎ 例：已知方程的两根都大于，则的取值范围是（　　）‎ A. B. C. D.或 ‎【答案】C ‎【解析】‎ 令，由题意可得，解得.‎ ‎【掌握练习】‎ ‎1、如果方程的两个实根一个大于‒2，另一个小于﹣2，那么实数m的取值范围是（　　）‎ A. B. C. D.（﹣1，5）‎ ‎【答案】D ‎2、已知二次方程两根都小于，则求实数的取值范围(   )‎ A. B. C. D.‎ ‎【答案】D ‎【解析】‎ 解：设，则，从而得。‎ 结论4：‎ 分布情况 两根都在内 两根有且仅有一根在内 ‎（图象有两种情况，只画了一种）‎ 一根在内，另一根在内， ‎ 大致图象（）‎ 得出的结论 或 大致图象（）‎ 得出的结论 或 综合结论（不讨论）‎ ‎——————‎ 例：方程的两根，且，则实数的范围 (   )‎ A. B. C. D.‎ ‎【答案】D ‎【解析】‎ 令，由得：，得，选D；‎ ‎【掌握练习】‎ ‎1、若关于的方程在内有解，则的取值范围是（ ）.‎ A. B. C. D.‎ ‎【答案】B ‎【解析】‎ 设，则，即，所以，故选B.‎ ‎2、关于的方程在区间内有两个不等实根,则实数的取值范围是(  )‎ A. B. C. D.‎ ‎【答案】C ‎ ‎