数学卷·2018届福建省莆田二十五中高二上学期期中数学试卷（理科）（解析版） 14页

‎2016-2017学年福建省莆田二十五中高二（上）期中数学试卷（理科）‎ ‎　‎ 一．选择题：（共12小题，每小题5分，共60分）．‎ ‎1．如果a＜b＜0，那么（　　）‎ A．a﹣b＞0 B．ac＜bc C． D．a2＜b2‎ ‎2．等差数列{an}中，a3=7，a9=19，则a5为（　　）‎ A．13 B．12 C．11 D．10‎ ‎3．已知{an}是等比数列，a2=2，a5=，则公比q=（　　）‎ A． B．﹣2 C．2 D．‎ ‎4．在△ABC中，若b=3，c=1，cosA=，则a=（　　）‎ A． B． C．8 D．12‎ ‎5．在△ABC中，内角A，B，C的对边分别为a，b，c，若a=3，b=4，C=120°，则△ABC的面积是（　　）‎ A．3 B． C．6 D．‎ ‎6．等差数列{an}中，a1=7，a3=3，前n项和为Sn，则n=（　　）时，Sn取到最大值．‎ A．4或5 B．4 C．3 D．2‎ ‎7．若ax2+x+a＜0的解集为∅，则实数a取值范围（　　）‎ A．a≥ B．a＜ C．﹣≤a≤ D．a≤﹣或a≥‎ ‎8．（5）若xy满足约束条件，则的取值范围为（　　）‎ A．[﹣，] B．[﹣，1] C．（﹣∞，﹣]∪[，+∞） D．（﹣∞，﹣]∪[1，+∞）‎ ‎9．各项都是正数的等比数列{an}，若a2， a3，2a1成等差数列，则的值为（　　）‎ A．2 B．2或﹣1 C． D．或﹣1‎ ‎10．已知函数的值域为（﹣∞，0]∪[4，+∞），则a的值是（　　）‎ A． B． C．1 D．2‎ ‎11．设等比数列{an}的前n项和为Sn，且S2=1，S4=3，则S6=（　　）‎ A．5 B．7 C．9 D．11‎ ‎12．设{an}（n∈N*）是等差数列，Sn是其前n项的和，且S5＜S6，S6=S7＞S8，则下列结论错误的是（　　）‎ A．d＜0 B．a7=0‎ C．S9＞S5 D．S6与S7均为Sn的最大值 ‎　‎ 二、填空题（共4小题，每小题5分，共20分）．‎ ‎13．若x，y满足约束条件由约束条件围成的图形的面积　　．‎ ‎14．若等差数列{an}的前n项和为Sn（n∈N*），若a2：a3=5：2，则S3：S5=　　．‎ ‎15．在△ABC中，角A、B、C所对边分别为a、b、c，若bcosC=ccosB成立，则△ABC是　　三角形．‎ ‎16．某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为　　元．‎ ‎　‎ 三、解答题（本大题共6小题，共70分）‎ ‎17．已知集合A={x|x2﹣5x﹣6＜0}，集合B={x|6x2﹣5x+1≥0}，集合C={x|（x﹣m）（x﹣m﹣9）＜0}‎ ‎（1）求A∩B；‎ ‎（2）若A⊆C，求实数 m的取值范围．‎ ‎18．等差数列{an}满足：a1=1，a2+a6=14；正项等比数列{bn}满足：b1=2，b3=8．‎ ‎（Ⅰ） 求数列{an}，{bn}的通项公式an，bn；‎ ‎（Ⅱ）求数列{an•bn}的前n项和Tn．‎ ‎19．已知数列{an}的前n项和Sn，且Sn=2n2+3n；‎ ‎（1）求它的通项an．‎ ‎（2）若bn=，求数列{bn}的前n项和Tn．‎ ‎20．△ABC的内角A、B、C的对边分别为a、b、c．己知c=asinC﹣ccosA．‎ ‎（1）求A；‎ ‎（2）若a=2，△ABC的面积为，求b，c．‎ ‎21．已知{an}是公差为3的等差数列，数列{bn}满足b1=1，b2=，anbn+1+bn+1=nbn．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）求{bn}的前n项和．‎ ‎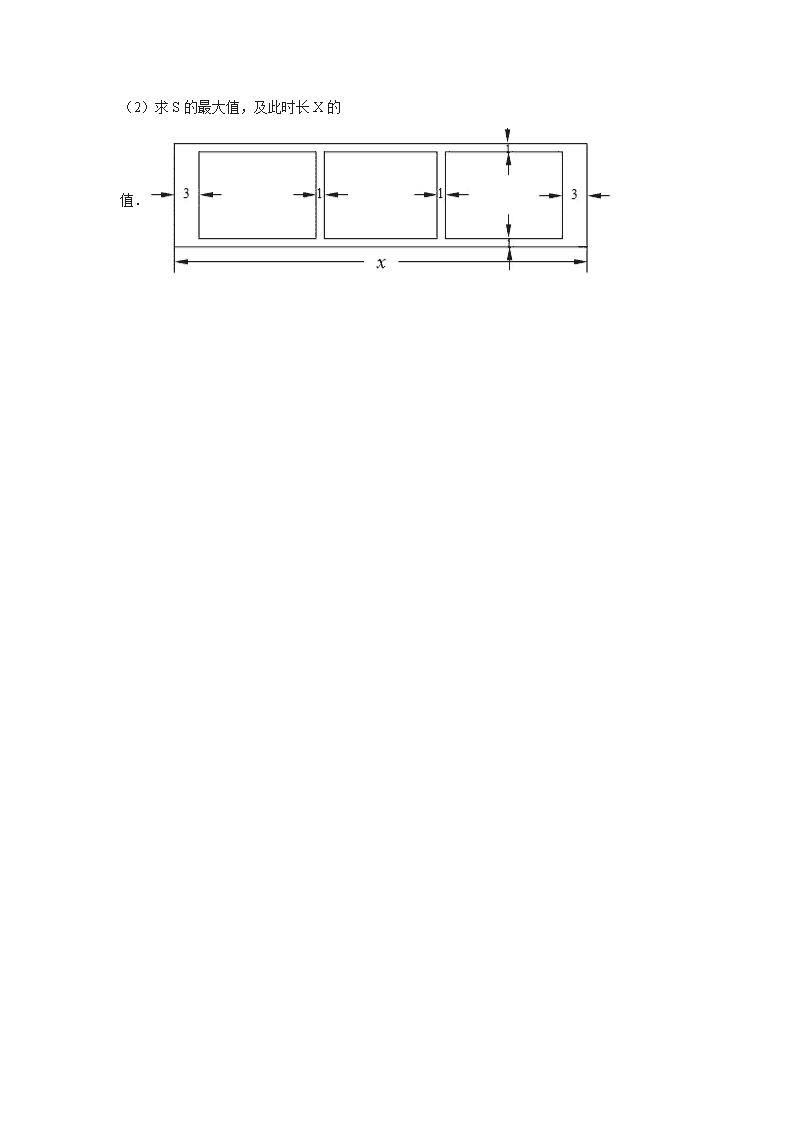22．某学校为了支持生物课程基地研究植物生长，计划利用学校空地建造一间室内面积为900m2的矩形温室，在温室内划出三块全等的矩形区域，分别种植三种植物，相邻矩形区域之间间隔1m，三块矩形区域的前、后与内墙各保留 1m 宽的通道，左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道，如图．设矩形温室的室内长为x（m），三块种植植物的矩形区域的总面积为S（m2）．‎ ‎（1）求S关于x的函数关系式；‎ ‎（2）求S的最大值，及此时长X的值．‎ ‎　‎ ‎2016-2017学年福建省莆田二十五中高二（上）期中数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一．选择题：（共12小题，每小题5分，共60分）．‎ ‎1．如果a＜b＜0，那么（　　）‎ A．a﹣b＞0 B．ac＜bc C． D．a2＜b2‎ ‎【考点】不等关系与不等式．‎ ‎【分析】根据a＜b＜0，给a，b，c赋予特殊值，即a=﹣2，b=﹣1，c=0，代入即可判定选项真假．‎ ‎【解答】解：∵a＜b＜0，给a，b，c赋予特殊值，即a=﹣2，b=﹣1，c=0‎ 选项A、B、D都不正确 故选C．‎ ‎　‎ ‎2．等差数列{an}中，a3=7，a9=19，则a5为（　　）‎ A．13 B．12 C．11 D．10‎ ‎【考点】等差数列的通项公式．‎ ‎【分析】根据公式a3=a1+2d=7，a9=a1+8d=19，可求a1，d，代入等差数列的通项公式可求．‎ ‎【解答】解：根据公式a3=a1+2d=7，a9=a1+8d=19，‎ 解方程得到 故a5=a1+4d=11，‎ 故选C ‎　‎ ‎3．已知{an}是等比数列，a2=2，a5=，则公比q=（　　）‎ A． B．﹣2 C．2 D．‎ ‎【考点】等比数列．‎ ‎【分析】根据等比数列所给的两项，写出两者的关系，第五项等于第二项与公比的三次方的乘积，代入数字，求出公比的三次方，开方即可得到结果．‎ ‎【解答】解：∵{an}是等比数列，a2=2，a5=，‎ 设出等比数列的公比是q，‎ ‎∴a5=a2•q3，‎ ‎∴==，‎ ‎∴q=，‎ 故选：D．‎ ‎　‎ ‎4．在△ABC中，若b=3，c=1，cosA=，则a=（　　）‎ A． B． C．8 D．12‎ ‎【考点】余弦定理．‎ ‎【分析】直接利用余弦定理即可计算求值得解．‎ ‎【解答】解：∵b=3，c=1，cosA=，‎ ‎∴由余弦定理可得：a2=b2+c2﹣2bccosA=9+1﹣2×=8，解得：a=2．‎ 故选：B．‎ ‎　‎ ‎5．在△ABC中，内角A，B，C的对边分别为a，b，c，若a=3，b=4，C=120°，则△ABC的面积是（　　）‎ A．3 B． C．6 D．‎ ‎【考点】正弦定理．‎ ‎【分析】由a，b及sinC的值，利用三角形的面积公式即可求出三角形ABC的面积．‎ ‎【解答】解：∵a=3，b=4，C=120°，‎ ‎∴S△ABC=absinC=×3×4×=3．‎ 故选B ‎　‎ ‎6．等差数列{an}中，a1=7，a3=3，前n项和为Sn，则n=（　　）时，Sn取到最大值．‎ A．4或5 B．4 C．3 D．2‎ ‎【考点】等差数列的前n项和．‎ ‎【分析】由已知条件推导出d=﹣2，从而得到Sn=﹣n2+8n，由此利用配方法能求出n=4时，Sn取到最大值．‎ ‎【解答】解：等差数列{an}中，‎ ‎∵a1=7，a3=3，∴7+2d=3，解得d=﹣2，‎ ‎∴Sn=7n+=﹣n2+8n=﹣（n2﹣8n）=﹣（n﹣4）2+16，‎ ‎∴n=4时，Sn取到最大值．‎ 故选：B．‎ ‎　‎ ‎7．若ax2+x+a＜0的解集为∅，则实数a取值范围（　　）‎ A．a≥ B．a＜ C．﹣≤a≤ D．a≤﹣或a≥‎ ‎【考点】一元二次不等式的解法．‎ ‎【分析】理解题意，即该不等式无实解．‎ ‎【解答】解：∵ax2+x+a＜0的解集为∅，‎ ‎∴a＞0，△≤0，即a＞0，1﹣4a2≤0，‎ 解得a≥．‎ 故选：A．‎ ‎　‎ ‎8．（5）若xy满足约束条件，则的取值范围为（　　）‎ A．[﹣，] B．[﹣，1] C．（﹣∞，﹣]∪[，+∞） D．（﹣∞，﹣]∪[1，+∞）‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作出可行域，结合的几何意义，即可行域内的动点与定点P（1，﹣1）连线的斜率求得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 的几何意义为可行域内的动点与定点P（1，﹣1）连线的斜率，‎ ‎∵，，‎ ‎∴的取值范围为[]．‎ 故选：B．‎ ‎　‎ ‎9．各项都是正数的等比数列{an}，若a2， a3，2a1成等差数列，则的值为（　　）‎ A．2 B．2或﹣1 C． D．或﹣1‎ ‎【考点】等差数列与等比数列的综合．‎ ‎【分析】设等比数列{an}的公比为q，由题意得q＞0，根据条件和等差中项的性质列出方程求出q的值，利用等比数列的通项公式化简即可得答案．‎ ‎【解答】解：设等比数列{an}的公比为q，则q＞0，‎ 因为a2， a3，2a1成等差数列，‎ 所以2×a3=a2+2a1，则，‎ 即q2﹣q﹣2=0，解得q=2或q=﹣1（舍去），‎ 所以===，‎ 故选：C．‎ ‎　‎ ‎10．已知函数的值域为（﹣∞，0]∪[4，+∞），则a的值是（　　）‎ A． B． C．1 D．2‎ ‎【考点】函数的值域．‎ ‎【分析】利用勾勾函数的性质求解．，当x＞0时，y的最小值为2，当x＜0时，y的最大值为﹣2，可得答案．‎ ‎【解答】解：由题意：函数的定义域为（﹣∞，0）∪（0，+∞），值域为（﹣∞，0]∪[4，+∞），‎ 令，当x＞0，a＞0时，y的最小值2，‎ 则当x＞0，a＞0时，的最小值为2+2，‎ 由题意：，解得a=1．满足题意．‎ 当x＜0，a＞0时，y的最大值为﹣2+2，‎ 由题意：﹣2+2=﹣1，解得a=1．满足题意．‎ 因此得a=1．‎ 故选：C．‎ ‎　‎ ‎11．设等比数列{an}的前n项和为Sn，且S2=1，S4=3，则S6=（　　）‎ A．5 B．7 C．9 D．11‎ ‎【考点】等比数列的性质．‎ ‎【分析】由等比数列的性质可得S2，S4﹣S2，S6﹣S4成等比数列，代入数据计算可得．‎ ‎【解答】解：由等比数列的性质可得S2，S4﹣S2，S6﹣S4成等比数列，‎ 即1，3﹣1，S6﹣3成等比数列，‎ ‎∴22=1×（S6﹣3），解得S6=7．‎ 故选：B．‎ ‎　‎ ‎12．设{an}（n∈N*）是等差数列，Sn是其前n项的和，且S5＜S6，S6=S7＞S8，则下列结论错误的是（　　）‎ A．d＜0 B．a7=0‎ C．S9＞S5 D．S6与S7均为Sn的最大值 ‎【考点】等差数列的前n项和．‎ ‎【分析】利用结论：n≥2时，an=sn﹣sn﹣1，易推出a6＞0，a7=0，a8＜0，然后逐一分析各选项，排除错误答案．‎ ‎【解答】解：由S5＜S6得a1+a2+a3+…+a5＜a1+a2++a5+a6，即a6＞0，‎ 又∵S6=S7，‎ ‎∴a1+a2+…+a6=a1+a2+…+a6+a7，‎ ‎∴a7=0，故B正确；‎ 同理由S7＞S8，得a8＜0，‎ ‎∵d=a7﹣a6＜0，故A正确；‎ 而C选项S9＞S5，即a6+a7+a8+a9＞0，可得2（a7+a8）＞0，由结论a7=0，a8＜0，显然C选项是错误的．‎ ‎∵S5＜S6，S6=S7＞S8，∴S6与S7均为Sn的最大值，故D正确；‎ 故选C．‎ ‎　‎ 二、填空题（共4小题，每小题5分，共20分）．‎ ‎13．若x，y满足约束条件由约束条件围成的图形的面积　　．‎ ‎【考点】简单线性规划．‎ ‎【分析】由约束条件作出可行域，求出三角形顶点的坐标，进一步求出|AB|，C到AB所在直线的距离，代入三角形面积公式得答案．‎ ‎【解答】解：由约束条件作出可行域如图，‎ 联立，得A（﹣2，﹣1），‎ 联立，得B（1，），‎ ‎∴|AB|=．‎ 又C（0，1）到直线x﹣2y=0的距离d=，‎ ‎∴由约束条件围成的图形的面积S==．‎ 故答案为：．‎ ‎　‎ ‎14．若等差数列{an}的前n项和为Sn（n∈N*），若a2：a3=5：2，则S3：S5=　3：2　．‎ ‎【考点】等差数列的性质．‎ ‎【分析】等差数列{an}中，由等差数列的通项公式表示出a2与a3，求出（a1+d）与（a1+2d）之比，再利用求和公式表示出S3与S5，利用比例的性质即可求出S3与S5比值．‎ ‎【解答】解：∵a2=a1+d，a3=a1+2d，a2：a3=5：2，‎ ‎∴（a1+d）：（a1+2d）=5：2，‎ ‎∵S3=3a1+d=3（a1+d），S5=5a1+d=5（a1+d），‎ 则S3：S5=3（a1+d）：5（a1+d）=15：10=3：2．‎ 故答案为：3：2‎ ‎　‎ ‎15．在△ABC中，角A、B、C所对边分别为a、b、c，若bcosC=ccosB成立，则△ABC是　等腰　三角形．‎ ‎【考点】正弦定理；两角和与差的余弦函数．‎ ‎【分析】运用正弦定理，化简ccosB=bcosC，即sinCcosB=sinBcosC⇒sin（B﹣C）=0，B=C，推出三角形的形状．‎ ‎【解答】解：∵bcosC=ccosB，‎ ‎∴sinCcosB=sinBcosC，‎ ‎∴sin（B﹣C）=0，‎ ‎∴B=C，‎ ‎∴三角形是等腰三角形．‎ 故答案为：等腰．‎ ‎　‎ ‎16．某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为　216000　元．‎ ‎【考点】简单线性规划的应用．‎ ‎【分析】设A、B两种产品分别是x件和y件，根据题干的等量关系建立不等式组以及目标函数，利用线性规划作出可行域，通过目标函数的几何意义，求出其最大值即可；‎ ‎【解答】解：（1）设A、B两种产品分别是x件和y件，获利为z元．‎ 由题意，得，z=2100x+900y．‎ 不等式组表示的可行域如图：由题意可得，解得：，A（60，100），‎ 目标函数z=2100x+900y．经过A时，直线的截距最大，目标函数取得最大值：2100×60+900×100=216000元．‎ 故答案为：216000．‎ ‎　‎ 三、解答题（本大题共6小题，共70分）‎ ‎17．已知集合A={x|x2﹣5x﹣6＜0}，集合B={x|6x2﹣5x+1≥0}，集合C={x|（x﹣m）（x﹣m﹣9）＜0}‎ ‎（1）求A∩B；‎ ‎（2）若A⊆C，求实数 m的取值范围．‎ ‎【考点】集合的包含关系判断及应用；交集及其运算．‎ ‎【分析】（1）由A={x|x2﹣5x﹣6＜0}={x|﹣1＜x＜6}，集合B={x|6x2﹣5x+1≥0}={x|x≥，或x≤}，能求出A∩B．‎ ‎（2）由A⊆C，建立不等式组，能求出m的取值范围．‎ ‎【解答】解：（1）∵A={x|x2﹣5x﹣6＜0}={x|﹣1＜x＜6}，‎ 集合B={x|6x2﹣5x+1≥0}={x|x≥，或x≤}，‎ ‎∴A∩B={x|﹣1＜x≤，或≤x＜6}．‎ ‎（2）∵集合C={x|（x﹣m）（x﹣m﹣9）＜0}={x|m＜x＜m+9}，A⊆C，‎ ‎∴，‎ 解得﹣3≤m≤﹣1．‎ ‎∴m的取值范围是{m|﹣3≤m≤﹣1}．‎ ‎　‎ ‎18．等差数列{an}满足：a1=1，a2+a6=14；正项等比数列{bn}满足：b1=2，b3=8．‎ ‎（Ⅰ） 求数列{an}，{bn}的通项公式an，bn；‎ ‎（Ⅱ）求数列{an•bn}的前n项和Tn．‎ ‎【考点】数列的求和．‎ ‎【分析】（Ⅰ）利用等差数列与等比数列的通项公式即可得出；‎ ‎（Ⅱ）由（I）有，利用“错位相减法”与等比数列的前n项和公式即可得解．‎ ‎【解答】解：（Ⅰ）设等差数列{an}的公差为d，‎ ‎∵a1=1，a2+a6=14；‎ ‎∴2×1+6d=14，解得d=2．‎ ‎∴an=1+2（n﹣1）=2n﹣1．‎ 设正项等比数列{bn}的公比为q＞0，‎ ‎∵b1=2，b3=8．‎ ‎∴2q2=8，解得q=2．‎ ‎∴bn=2×2n﹣1=2n．‎ 因此数列{an}，{bn}的通项公式．‎ ‎（II）由（I）有，‎ 两式相减，得=，‎ ‎∴．‎ ‎　‎ ‎19．已知数列{an}的前n项和Sn，且Sn=2n2+3n；‎ ‎（1）求它的通项an．‎ ‎（2）若bn=，求数列{bn}的前n项和Tn．‎ ‎【考点】数列的求和；等差数列的性质．‎ ‎【分析】（1）由数列的通项和求和的关系：当n=1时，a1=S1，当n＞1时，an=Sn﹣Sn﹣1，化简即可得到所求通项；‎ ‎（2）求得bn===（﹣），再由数列的求和方法：裂项相消求和，化简整理即可得到所求和．‎ ‎【解答】解：（1）由Sn=2n2+3n，‎ 当n=1时，a1=S1=5；‎ 当n＞1时，an=Sn﹣Sn﹣1=2n2+3n﹣2（n﹣1）2﹣3（n﹣1）‎ ‎=4n+1，对n=1也成立．‎ 则通项an=4n+1；‎ ‎（2）bn===（﹣），‎ 即有前n项和Tn=（﹣+﹣+…+﹣）‎ ‎=（﹣）=．‎ ‎　‎ ‎20．△ABC的内角A、B、C的对边分别为a、b、c．己知c=asinC﹣ccosA．‎ ‎（1）求A；‎ ‎（2）若a=2，△ABC的面积为，求b，c．‎ ‎【考点】正弦定理；余弦定理．‎ ‎【分析】（1）由c=asinC﹣ccosA，由正弦定理可得：sinC=sinAsinC﹣sinCcosA，化为=，即可得出．‎ ‎（2）由a=2，△ABC的面积为，可得bc=4．由余弦定理可得：，化为b+c=4．联立解出即可．‎ ‎【解答】解：（1）∵△ABC中，c=asinC﹣ccosA，‎ 由正弦定理可得：sinC=sinAsinC﹣sinCcosA，‎ ‎∵sinC≠0，∴1=sinA﹣cosA=2，‎ 即=，∵∈，‎ ‎∴=，‎ ‎∴A=．‎ ‎（2）∵a=2，△ABC的面积为，‎ ‎∴，化为bc=4．‎ 由余弦定理可得：，‎ 化为b+c=4．‎ 联立，解得b=c=2．‎ ‎∴b=c=2．‎ ‎　‎ ‎21．已知{an}是公差为3的等差数列，数列{bn}满足b1=1，b2=，anbn+1+bn+1=nbn．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）求{bn}的前n项和．‎ ‎【考点】数列递推式．‎ ‎【分析】（Ⅰ）令n=1，可得a1=2，结合{an}是公差为3的等差数列，可得{an}的通项公式；‎ ‎（Ⅱ）由（1）可得：数列{bn}是以1为首项，以为公比的等比数列，进而可得：{bn}的前n项和．‎ ‎【解答】解：（Ⅰ）∵anbn+1+bn+1=nbn．‎ 当n=1时，a1b2+b2=b1．‎ ‎∵b1=1，b2=，‎ ‎∴a1=2，‎ 又∵{an}是公差为3的等差数列，‎ ‎∴an=3n﹣1，‎ ‎（Ⅱ）由（I）知：（3n﹣1）bn+1+bn+1=nbn．‎ 即3bn+1=bn．‎ 即数列{bn}是以1为首项，以为公比的等比数列，‎ ‎∴{bn}的前n项和Sn==（1﹣3﹣n）=﹣．‎ ‎　‎ ‎22．某学校为了支持生物课程基地研究植物生长，计划利用学校空地建造一间室内面积为900m2的矩形温室，在温室内划出三块全等的矩形区域，分别种植三种植物，相邻矩形区域之间间隔1m，三块矩形区域的前、后与内墙各保留 1m 宽的通道，左、右两块矩形区域分别与相邻的左右内墙保留 3m 宽的通道，如图．设矩形温室的室内长为x（m），三块种植植物的矩形区域的总面积为S（m2）．‎ ‎（1）求S关于x的函数关系式；‎ ‎（2）求S的最大值，及此时长X的值．‎ ‎【考点】函数解析式的求解及常用方法．‎ ‎【分析】（1）根据题意，室内面积为900m2的矩形，长为x（m），则宽为：，三块种植植物的矩形长度为x﹣8，则宽为，植植物的矩形区域的总面积为S=长×宽，可得S关于x的函数关系式．‎ ‎（2）利用基本不等式的性质求解S的最大值以及长度x的值．‎ ‎【解答】解：（1）由题意：室内面积为900m2的矩形，长为x（m），则宽为：，‎ 三块种植植物的矩形长度为x﹣8，则宽为，‎ 植物的矩形区域的总面积为S=，‎ ‎（2）由（1）可得S=，‎ 化简可得：S=916﹣（2x），‎ ‎∵2x≥2=240，（当且仅当x=60时取等号）‎ ‎∴Smax=916﹣240=676（m2）‎ 此时长为x=60．‎ 故得S的最大值676平方米，长度为60米．‎ ‎　‎