2020届二轮复习 用样本的频率分布估计总体分布 课件（24张）（全国通用） 24页

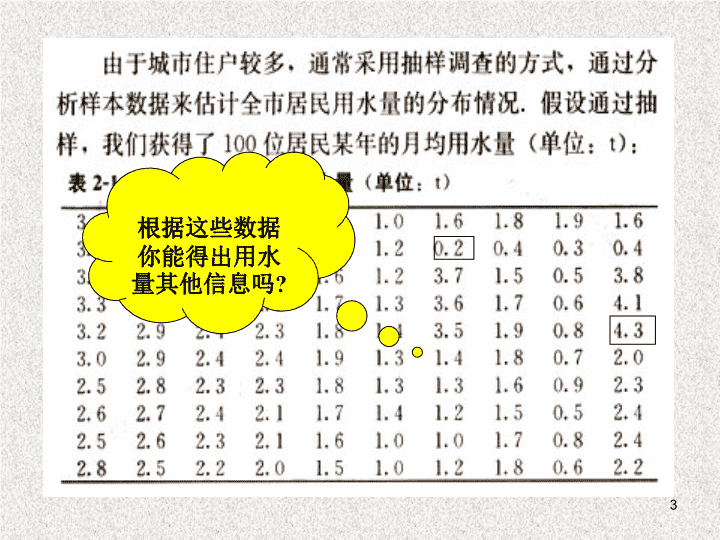
1 知识点： 1. 频率分布表、频率分布直方图、 频率折线图和茎叶图 2. 会分析样本的分布，准确的作出总体估计 教学重点：会列频率分布表，画频率分布直方图、 频率折线图和茎叶图 教学难点：能通过样本的频率分布估计总体的分布 2 3 根据这些数据你能得出用水量其他信息吗 ? 4 1 、求极差 ( 即一组数据中最大值与最小值的差 ) 知道这组数据的变动范围 4.3-0.2=4.1 2 、决定组距与组数（将数据分组） 3 、 将数据分组 (8.2 取整 , 分为 9 组 ) 画频率分布直方图的步骤 4 、列出 频率分布表 .( 学生填写频率 / 组距一栏 ) 5 、画出 频率分布直方图 。 组距 ： 指每个小组的两个端点的距离，组距 组数 ： 将数据分组，当数据在 100 个以内时， 按数据多少常分 5-12 组。 5 频率分布直方图如下 ： 月均用水量 /t 频率 组距 0.10 0.20 0.30 0.40 0.50 0.5 1 1.5 2 2.5 3 3.5 4 4.5 小长方形的面积 =? 6 频率分布直方图如下 ： 月均用水量 /t 频率 组距 0.10 0.20 0.30 0.40 0.50 0.5 1 1.5 2 2.5 3 3.5 4 4.5 小长方形的面积总和 =? 7 频率分布直方图如下 ： 月均用水量 /t 频率 组距 0.10 0.20 0.30 0.40 0.50 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月均用水量最多的在那个区间 ? 8 频率分布直方图如下 ： 月均用水量 /t 频率 组距 0.10 0.20 0.30 0.40 0.50 0.5 1 1.5 2 2.5 3 3.5 4 4.5 请大家阅读第 68 页 , 直方图有那些优点和缺点 ? 9 练 习 1. 有一个容量为 50 的样本数据的分组的频数如下： ［ 12.5, 15.5 ） 3 ［ 15.5, 18.5 ） 8 ［ 18.5, 21.5 ） 9 ［ 21.5, 24.5 ） 11 ［ 24.5, 27.5 ） 10 ［ 27.5, 30.5 ） 5 ［ 30.5, 33.5 ） 4 (1) 列出样本的频率分布表 ; (2) 画出频率分布直方图 ; (3) 根据频率分布直方图估计 , 数据落在 [15.5, 24.5 ）的百分比是多少 ? 10 解 : 组距为 3 分组 频数 频率 频率 / 组距 ［ 12.5, 15.5 ） 3 ［ 15.5, 18.5 ） 8 ［ 18.5, 21.5 ） 9 ［ 21.5, 24.5 ） 11 ［ 24.5, 27.5 ） 10 ［ 27.5, 30.5 ） 5 ［ 30.5, 33.5 ） 4 0.06 0.16 0.18 0.22 0.20 0.10 0.08 0.020 0.053 0.060 0.073 0.067 0.033 0.027 (2) 纵坐标为 : 注意 : 11 频率分布直方图如下 ： 频率 组距 0.010 0.020 0.030 0.040 0.050 12.5 15.5 0.060 0.070 12 频率分布直方图如下 ： 月均用水量 /t 频率 组距 0.10 0.20 0.30 0.40 0.50 0.5 1 1.5 2 2.5 3 3.5 4 4.5 连接频率分布直方图中各小长方形上端的中点 , 得到 频率分布折线图 13 利用样本频分布对总体分布进行相应估计 （ 3 ）当样本容量无限增大，组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线 —— 总体密度曲线 。 （ 2 ）样本容量越大，这种估计越精确。 （ 1 ）上例的样本容量为 100 ，如果增至 1000 ，其频率分布直方图的情况会有什么变化？假如增至 10000 呢？ 14 2.2 总体分布的估计 频率 组距 月均用水量 （ mm ） a b 当样本容量无限增大，分组的组距无限缩小，那么频率分 布直方图就会无限接近一条光滑曲线 —— 总体密度曲线 ． 总体在区间 内取值的概率 S 15 总体密度曲线 频率 组距 月均用水量 /t a b （图中阴影部分的面积，表示总体在某个区间 (a, b) 内取值的百分比）。 16 用样本分布直方图去估计相应的总体分布时，一般样本容量越大， 频率分布直方图 就会无限接近 总体密度曲线 ，就越精确地反映了总体的分布规律，即越精确地反映了总体在各个范围内取值百分比。 总体密度曲线反映了总体在各个范围内取值的百分比 , 精确地反映了总体的分布规律。是研究总体分布的工具 . 总体密度曲线 17 茎叶图 情境： 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下： (1) 甲运动员得分： 13,51,23,8,26,38,16,33,14,28,39 (2) 乙运动员得分 ： 49,24,12,31,50,31,44,36,15,37,25,36,39 问题： 如何有条理地列出这些数据，分析该运动员的整体水平及发挥的稳定程度？ 18 茎叶图 甲 乙 0 1 2 3 4 5 2 5 5 4 1 6 1 6 7 9 4 9 0 8 4 6 3 6 8 3 8 9 1 19 一般地：当数据是一位和两位有效数字时，用中间的数字表示十位数，即第一个有效数字，两边的数字表示个位数，即第二个有效数字，它的中间部分像植物的茎，两边部分像植物茎上长出来的叶子，因此通常把这样的图叫做茎叶图。茎按从小到大的顺序从上向下列出，共茎的叶一般按从大到小（或从小到大）的顺序同行列出。 1 ．茎叶图的概念： 20 2 ．茎叶图的特征： １）用茎叶图表示数据有两个优点：一是从统计图上没有原始数据信息的损失，所有数据信息都可以从茎叶图中得到；二是茎叶图中的数据可以随时记录，随时添加，方便记录与表示；（２）茎叶图只便于表示两位（或一位）有效数字的数据，对位数多的数据不太容易操作；而且茎叶图只方便记录两组的数据，两个以上的数据虽然能够记录，但是没有表示两个记录那么直观，清晰；（３）茎叶图对重复出现的数据要重复记录，不能遗漏 ． 21 制作茎叶图的方法是 ：将所有两位数的十位数字作为 “ 茎 ” ，个位数字作为 “ 叶 ” ，茎相同者共用一个茎，茎按从小到大的顺序从上向下列出，共茎的叶一般按从大到小（或从小到大）的顺序同行列出 . 茎叶图的制作方法 注意 ： 在制作茎叶图时，重复出现的数据要重复记录，不能遗漏，特别是 “ 叶 ” 部分；同一数据出现几次，就要在图中体现几次 . 22 用茎叶图表示数据有两个突出的优点： 一 . 是所有的信息都可以从这个茎叶图 上得到； 二 . 是茎叶图便于记录和表示 . 用茎叶图表示数据有一个突出的缺点： 茎叶图 的缺点 是其分析只是粗略的，对差异不大的两组数据不易分析；表示三位数以上的数据时不够方便 . 23 1 、求极差 ( 即一组数据中最大值与最小值的差 ) 知道这组数据的变动范围 4.3-0.2=4.1 2 、决定组距与组数（将数据分组） 3 、 将数据分组 (8.2 取整 , 分为 9 组 ) 小结 : 一 . 画频率分布直方图的步骤 4 、列出 频率分布表 .( 填写频率 / 组距一栏 ) 5 、画出 频率分布直方图 。 组距 ： 指每个小组的两个端点的距离，组距 组数 ： 将数据分组，当数据在 100 个以内时， 按数据多少常分 5-12 组。 ( 注意 ) 纵坐标为 : 24 二 . 总体密度曲线 1. 当样本容量无限增大，组距无限缩小，那么频率分布直方图就会无限接近于一条光滑曲线 —— 总体密度曲线 。 2. 用样本分布直方图去估计相应的总体分布时，一般样本容量越大， 频率分布直方图 就会无限接近 总体密度曲线 ，就越精确地反映了总体的分布规律，即越精确地反映了总体在各个范围内取值百分比。