2017高考数学（理,江苏）二轮专题复习与策略（教师用书） 第1部分 专题2 第8讲 三角函数的图象与性质 8页

第8讲　三角函数的图象与性质 题型一| 三角函数的概念及其基本关系、诱导公式 ‎　(1)已知cos＝，则sin＝________.‎ ‎(2)已知角θ的顶点在坐标原点，始边与x轴正半轴重合，终边在直线3x－y＝0上，则＝________.‎ ‎ (3)(2016·合肥模拟)如图8－1，为了研究钟表与三角函数的关系，建立如图所示的坐标系，设秒针针尖位置P(x，y)．若初始位置为P0，当秒针从P0(此时t＝0)正常开始走时，那么点P的纵坐标y与时间t的函数关系是________．‎ 图8－1‎ ‎(1)　(2)　(3)y＝sin　[(1)由题意得：sin＝sin ‎＝cos＝.‎ ‎(2)根据直线的斜率的定义得tan θ＝3，＝＝＝.‎ ‎(3)由三角函数的定义可知，初始位置点P0的弧度为，由于秒针每秒转过的弧度为－，针尖位置P到坐标原点的距离为1，故点P的纵坐标y与时间t的函数关系可能为y＝sin.]‎ ‎【名师点评】　1.涉及与圆及角有关的函数建模问题(如钟表、摩天轮、水车等)，常常借助三角函数的定义求解．应用定义时，注意三角函数值仅与终边位置有关，与终边上点的位置无关．‎ ‎2．应用诱导公式时要弄清三角函数在各个象限内的符号；利用同角三角函数的关系化简过程要遵循一定的原则，如切化弦、化异为同、化高为低、化繁为简等．‎ ‎1．(2016·南通调研一)已知sin＝，则 sin＋sin2的值是________．‎ 　[sin＋sin2＝sin＋sin2＝－sin＋1－sin2＝.]‎ ‎2．如图8－2，以Ox为始边作角α(0＜α＜π)，终边与单位圆相交于点P，已知点P的坐标为，则＝________.‎ 图8－2‎ 　[由三角函数定义，‎ 得cos α＝－，sin α＝，‎ ‎∴原式＝ ‎＝ ‎＝2cos2α＝2×2＝.]‎ ‎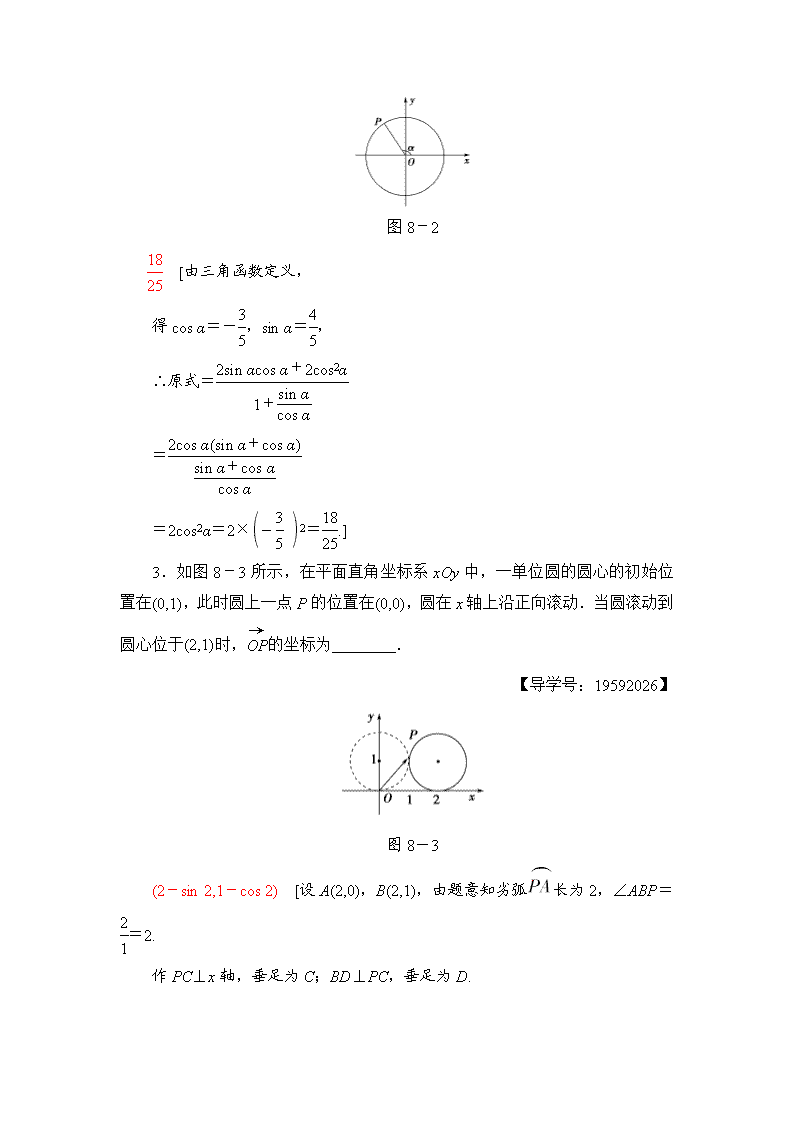3．如图8－3所示，在平面直角坐标系xOy中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P的位置在(0,0)，圆在x轴上沿正向滚动．当圆滚动到圆心位于(2,1)时，的坐标为________．‎ ‎【导学号：19592026】‎ 图8－3‎ ‎(2－sin 2,1－cos 2)　[设A(2,0)，B(2,1)，由题意知劣弧长为2，∠ABP＝＝2.‎ 作PC⊥x轴，垂足为C；BD⊥PC，垂足为D.‎ ‎∴∠PBD＝2－.‎ 设P(x，y)，由三角函数定义，‎ x＝2－1×cos＝2－sin 2，‎ y＝1＋1×sin＝1－cos 2，‎ ‎∴的坐标为(2－sin 2,1－cos 2)．]‎ 题型二| 三角函数的图象及应用 ‎　(1)函数y＝sin的图象可由函数y＝sin x的图象作两次变换得到，第一次变换是针对函数y＝sin x的图象而言的，第二次变换是针对第一次变换所得图象而言的，现给出下列四个变换：‎ A．图象上所有点向右平移个单位；‎ B．图象上所有点向右平移个单位；‎ C．图象上所有点的横坐标变为原来的2倍(纵坐标不变)；‎ D．图象上所有点的横坐标变为原来的倍(纵坐标不变)．‎ 请按顺序写出两次变换的代表字母：________.‎ ‎(2)函数f(x)＝Asin(ωx＋φ)(A，ω，φ为常数，A>0，ω>0,0<φ<π)的图象如图8－4所示，则f的值为________．‎ 图8－4‎ ‎(1)BD或DA　(2)1　[(1)由函数y＝sin x的图象上所有点向右平移个单位，可得函数y＝sin，再将图象上所有点的横坐标变为原来的倍，得函数y＝sin，则两次变换依次为BD.‎ 或，由函数y＝sin x的图象上所有点的横坐标变为原来的倍，可得函数y＝sin 2x，再将图象上所有点向右平移个单位，则两次变换依次为DA.‎ ‎(2)由图知：A＝2，＝－，T＝π，ω＝＝2.又函数过点，所以有sin＝1，而0<φ<π，所以φ＝.‎ 所以f(x)＝2sin，因此f＝2sin ‎＝1.]‎ ‎【名师点评】　作三角函数图象左右平移变换时，平移的单位数是指单个变量x的变化量，因此由y＝sin ωx(ω>0)的图象得到y＝sin(ωx＋φ)的图象时，应将图象上所有点向左(φ>0)或向右(φ<0)平移个单位，而非|φ|个单位．‎ ‎1．(2016·苏北三市三模)已知函数f(x)＝sin x(x∈[0，π])和函数g(x)＝tan x 的图象交于A，B，C三点，则△ABC的面积为________．‎ π　[由sin x＝tan x得cos x＝，又x∈[0，π]，∴x＝，又f＝sin＝.‎ 不妨设A(0,0)，B，C(π，0)，‎ ‎∴S△ABC＝×π×＝π.]‎ ‎2．将函数f(x)＝2sin(ω>0)的图象向左平移个单位，得到函数y＝g(x)的图象，若y＝g(x)在上为增函数，则ω的最大值为________．‎ ‎2　[平移后的解析式为g(x)＝2sin＝2sin ωx，此函数的单调递增区间为－≤x≤＋，故⊆(k∈Z)，即由①式得k≤，由②式得0<ω≤‎ ‎8k＋2，因为k∈Z且要求ω的最大值，则k＝0，故ω的最大值为2.]‎ ‎3．函数f(x)＝cos(ωx＋φ)的部分图象如图8－5所示，则f(x)的单调递减区间为________．‎ 图8－5‎ ，k∈Z　[由图象知，周期T＝2＝2，‎ ‎∴＝2，∴ω＝π.‎ 由π×＋φ＝＋2kπ，k∈Z，不妨取φ＝，‎ ‎∴f(x)＝cos.‎ 由2kπ<πx＋<2kπ＋π，k∈Z，得2k－0)的最大值与最小正周期相同，则函数f(x)在[－1,1]上的单调增区间为________．‎ ‎(1)　(2)　[(1)因为三角函数的对称轴经过最值点，所以当x＝时，f(x)＝sin(x＋θ)取最值，即sin＝±1⇒＋θ＝＋kπ，(k∈Z)，又0<θ<，所以θ＝.‎ ‎(2)由题意可知，函数f(x)＝2sin，令－＋2kπ≤πx－≤＋2kπ，解得－＋2k≤x≤＋2k，k∈Z，又x∈[－1,1]，所以－≤x≤，所以函数f(x)在[－1,1]上的单调递增区间为.]‎ ‎【名师点评】　函数y＝Asin(ωx＋φ)的性质及应用的求解思路：‎ 第一步：先借助三角恒等变换及相应三角函数公式把待求函数化成y＝Asin(ωx＋φ)＋B的形式；‎ 第二步：把“ωx＋φ”视为一个整体，借助复合函数性质求y＝Asin(ωx＋φ)＋B的单调性及奇偶性、最值、对称性等问题．‎ ‎1．(2016·南通二调)设函数y＝sin(0＜x＜π)，当且仅当x＝时，y取得最大值，则正数ω的值为________．‎ ‎2　[由0＜x＜π，当且仅当x＝时，y取得最大值，故即 ‎∴ω＝2.]‎ ‎2．若x是一个三角形的最小内角，则函数y＝sin x－cos x的值域是________．‎ 　[因为x是一个三角形的最小内角，所以 ‎0