数学卷·2017届江苏省兴化一中高三下学期期中考试（2017 11页

兴化市第一中学高三年级学情调研卷 高 三 数 学 命题人：耿小平 2017.04‎ 一、填空题：本大题共14小题，每小题5分，共70分．请把答案填写在答题卡相应位置上．‎ ‎1.已知为实数集，，则　 .‎ ‎2.命题:“,”的否定是 .‎ ‎3.已知（a∈R，为虚数单位），若复数z在复平面内对应的点在实轴上，则a= ．‎ ‎4.设不等式组，表示平面区域为D，在区域D内随机取一个 ‎ ‎ 点，则此点到坐标原点的距离大于2的概率是____ ____.‎ ‎5.阅读右图所示的程序框图，运行相应的程序，输出的值 ‎ 等于______.‎ ‎6.椭圆的右焦点为，右准线为，若过点且垂直于轴的弦的弦长等于点到的距离，则椭圆的离心率是 ． ‎ ‎7．已知正方形ABCD的边长为1，点E是AB边上的动点，则的最大值为______.‎ ‎8.设且若定义在区间内的函数是奇函数，则的取值范围是 .‎ ‎9.巳知函数有两个不同的零点，且方程有两个不同的实根.若把这四个数按从小到大排列构成等差数列，则实数m的值为____ ______.‎ ‎10.等比数列中，，函数，则曲线 ‎ 在点处的切线方程为 .‎ ‎11.已知变量，则的最小值为 .‎ ‎12.已知函数，其中．若函数仅在处有极值，则的取值范围是 ．‎ ‎13.已知成等差数列，将其中的两个数交换，得到的三个数依次成等比数列，则的值为 ．‎ ‎14.如图，用一块形状为半椭圆的铁皮截取一个以短轴为底的等腰梯形，记所得等腰梯形ABCD的面积为，则的最小值是 ．‎ 二、解答题：本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．‎ ‎15．（本小题满分14分）‎ 已知函数f(x)＝2sin(2x＋φ)(0＜φ＜2π)的图象过点(，－2)．‎ ‎（1）求φ的值；‎ ‎（2）若f()＝，－＜α＜0，求sin(2α－)的值．‎ ‎16．（本小题满分14分）‎ 如图，三棱柱ABC－A1B‎1C1中，M，N分别为AB，B‎1C1的中点．‎ ‎（1）求证：MN∥平面AA‎1C1C；‎ ‎（2）若CC1＝CB1，CA＝CB，平面CC1B1B⊥平面ABC，求证：AB^平面CMN．‎ A1‎ A B C B1‎ C1‎ M N ‎（第16题图）‎ ‎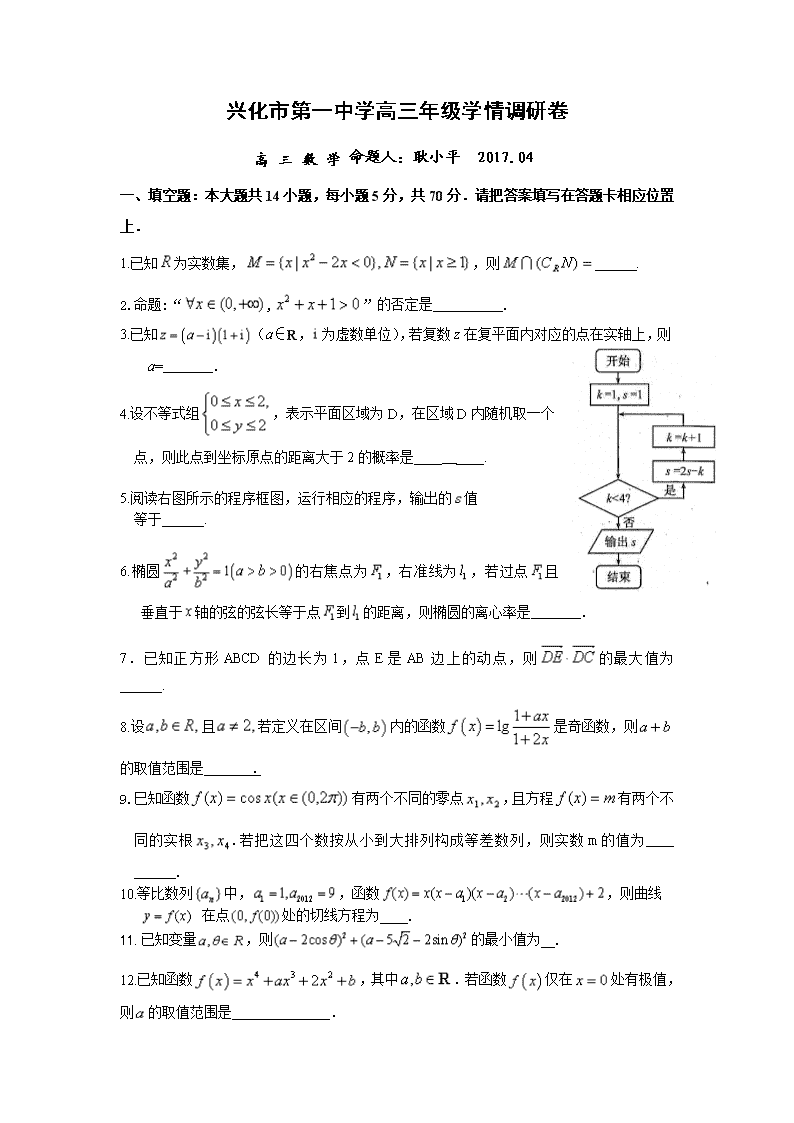17．（本小题满分15分）‎ 如图,椭圆经过点离心率,直线的方程为.‎ ‎(1) 求椭圆的方程;‎ ‎(2) 是经过右焦点的任一弦(不经过点),设直线与直线相交于点,记的斜率分别为问:是否存在常数,使得?若存在求的值;若不存在,说明理由.‎ ‎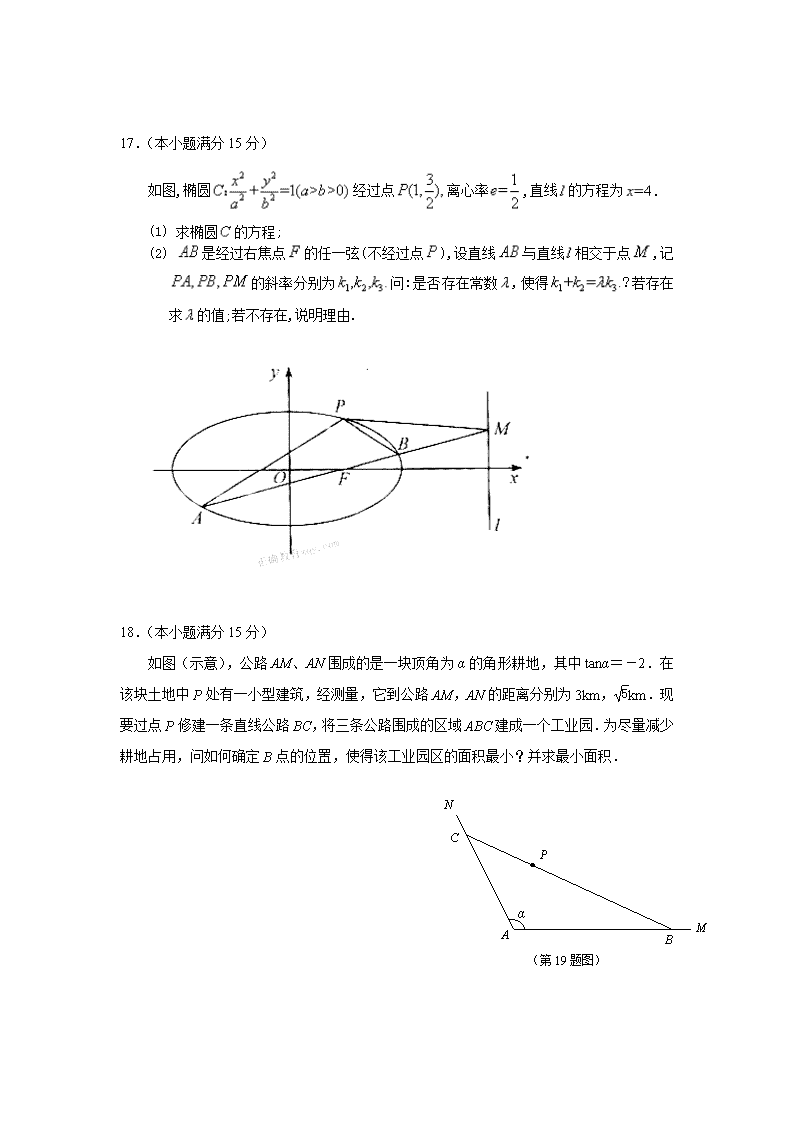18．（本小题满分15分）‎ 如图（示意），公路AM、AN围成的是一块顶角为α的角形耕地，其中tanα＝－2．在该块土地中P处有一小型建筑，经测量，它到公路AM，AN的距离分别为‎3km，km．现要过点P修建一条直线公路BC，将三条公路围成的区域ABC建成一个工业园．为尽量减少耕地占用，问如何确定B点的位置，使得该工业园区的面积最小？并求最小面积．‎ ‎·‎ A M N P ‎（第19题图）‎ α C B ‎ ‎ ‎19．（本小题满分16分）‎ 已知函数f(x)＝ax3＋|x－a|，aR．‎ ‎（1）若a＝－1，求函数y＝f(x) (x[0，＋∞))的图象在x＝1处的切线方程；‎ ‎（2）若g(x)＝x4，试讨论方程f(x)＝g(x)的实数解的个数；‎ ‎（3）当a＞0时，若对于任意的x1[a，a＋2]，都存在x2[a＋2，＋∞)，使得f(x1)f(x2)＝1024，求满足条件的正整数a的取值的集合．‎ ‎20．（本小题满分16分）‎ 已知数列{an}的各项均为正数，其前n项的和为Sn，且对任意的m，n∈N*，‎ 都有(Sm＋n＋S1)2＝‎4a2ma2n． ‎ ‎（1）求的值；‎ ‎（2）求证：{an}为等比数列；‎ ‎（3）已知数列{cn}，{dn}满足|cn|＝|dn|＝an，p(p≥3)是给定的正整数，数列{cn}，{dn}的前p项的和分别为Tp，Rp，且Tp＝Rp，求证：对任意正整数k(1≤k≤p)，ck＝dk．‎ 兴化市第一中学高三年级学情调研卷数学参考答案及评分标准 ‎ ‎2017.04 ‎ 一、填空题：本大题共14小题，每小题5分，共70分． ‎ ‎1. 2. 3.1‎ ‎4. 5. 6. ‎ ‎7. 1 8. 9.‎ ‎10. 11. 9 12.‎ ‎13．10 14.‎ 二、解答题：本大题共6小题，共计90分．‎ ‎15．（本小题满分14分）‎ 解：（1）因为函数f(x)＝2sin(2x＋φ)(0＜φ＜2π)的图象过点(，－2)，‎ 所以f()＝2sin(π＋φ)＝－2，‎ 即sinφ＝1． …………………………………………… 4分 因为0＜φ＜2π，所以φ＝． …………………………………………… 6分 ‎（2）由（1）得，f(x)＝2cos2x． ………………………………………… 8分 因为f()＝，所以cosα＝．‎ 又因为－＜α＜0，所以sinα＝－． …………………………………… 10分 所以sin2α＝2sinαcosα＝－，cos2α＝2cos2α－1＝－．…………………… 12分 从而sin(2α－)＝sin2αcos－cos2αsin＝． …………………… 14分 ‎16．（本小题满分14分）‎ 证明：（1）取A‎1C1的中点P，连接AP，NP．‎ A1‎ A B C B1‎ C1‎ M N ‎（第16题图）‎ P 因为C1N＝NB1，C1P＝PA1，所以NP∥A1B1，NP＝A1B1． …………………… 2分 在三棱柱ABC－A1B‎1C1中，A1B1∥AB，A1B1＝AB．‎ 故NP∥AB，且NP＝AB． ‎ 因为M为AB的中点，所以AM＝AB．‎ 所以NP＝AM，且NP∥AM．‎ 所以四边形AMNP为平行四边形．‎ 所以MN∥AP． ……………………………………… 4分 因为APÌ平面AA‎1C1C，MNË平面AA‎1C1C，‎ 所以MN∥平面AA‎1C1C． ……………………………………………… 6分 ‎（2）因为CA＝CB，M为AB的中点，所以CM⊥AB． …………………………… 8分 因为CC1＝CB1，N为B‎1C1的中点，所以CN⊥B‎1C1． ‎ 在三棱柱ABC－A1B‎1C1中，BC∥B‎1C1，所以CN^BC．‎ 因为平面CC1B1B⊥平面ABC，平面CC1B1B∩平面ABC＝BC．CNÌ平面CC1B1B，‎ 所以CN⊥平面ABC． …………………………………… 10分 因为ABÌ平面ABC，所以CN⊥AB． …………………………………… 12分 因为CMÌ平面CMN，CNÌ平面CMN，CM∩CN＝C，‎ 所以AB⊥平面CMN． …………………………………… 14分 ‎17. （本小题满分16分）‎ ‎【答案】解:(1)由在椭圆上得, ① ‎ 依题设知,则 ② ‎ ②代入①解得. ‎ 故椭圆的方程为. ……………………………5分 ‎(2)方法一:由题意可设的斜率为, ‎ 则直线的方程为 ③ ‎ 代入椭圆方程并整理,得, ‎ 设,则有 ‎ ‎ ④ ‎ 在方程③中令得,的坐标为. ‎ 从而. ‎ 注意到共线,则有,即有. ‎ 所以 ‎ ‎ ⑤ ……………………………11分 ④代入⑤得, ‎ 又,所以.故存在常数符合题意. …………………16分 ‎18．（本小题满分16分）‎ 解：（方法一）‎ ‎·‎ ‎(A)‎ x N P y O B C ‎（第19题图1）‎ 如图1，以A为原点，AB为x轴，建立平面直角坐标系．‎ 因为tanα＝－2，故直线AN的方程是y＝－2x．‎ 设点P(x0，y0)．‎ 因为点P到AM的距离为3，故y0＝3．‎ 由P到直线AN的距离为，‎ 得＝，解得x0＝1或x0＝－4(舍去)，‎ 所以点P(1，3)． ……………………………… 4分 显然直线BC的斜率存在．设直线BC的方程为y－3＝k(x－1)，k∈(－2，0)．‎ 令y＝0得xB＝1－． ……………………………… 6分 由解得yC＝． ……………………………… 8分 设△ABC的面积为S，则S＝×xB×yC＝＝－1＋． …………… 10分 ‎ 由S¢＝ ＝0得k＝－或k＝3．‎ 当－2＜k＜－时，S¢＜0，S单调递减；当－＜k＜0时，S¢＞0，S单调递增．… 13分 所以当k＝－时，即AB＝5时，S取极小值，也为最小值15． ‎ 答：当AB＝‎5km时，该工业园区的面积最小，最小面积为‎15km2．……………… 15分 ‎（方法二）‎ 如图1，以A为原点，AB为x轴，建立平面直角坐标系．‎ 因为tanα＝－2，故直线AN的方程是y＝－2x．‎ 设点P(x0，y0)．‎ 因为点P到AM的距离为3，故y0＝3．‎ 由P到直线AN的距离为，‎ 得＝，解得x0＝1或x0＝－4(舍去)，‎ 所以点P(1，3)． ……………………………… 4分 显然直线BC的斜率存在．设直线BC的方程为y－3＝k(x－1)，k∈(－2，0)．‎ 令y＝0得xB＝1－． ……………………………… 6分 由解得yC＝． ……………………………… 8分 设△ABC的面积为S，则S＝×xB×yC＝＝－1＋． …………… 10分 ‎ 令8k－9＝t，则t∈(－25，－9)，从而k＝． ‎ 因此S＝－1＋＝－1＋＝－1＋．………… 13分 因为当t∈(－25，－9)时，t＋∈(－34，－30]，‎ 当且仅当t＝－15时，此时AB＝5，34＋t＋的最大值为4．从而S有最小值为15．‎ 答：当AB＝‎5km时，该工业园区的面积最小，最小面积为‎15km2．……………… 15分 ‎（方法三）‎ 如图2，过点P作PE⊥AM，PF⊥AN，垂足为E、F，连接PA．设AB＝x，AC＝y．‎ ‎·‎ A M N P B C ‎（第19题图2）‎ E F 因为P到AM，AN的距离分别为3，，‎ ‎ 即PE＝3，PF＝．‎ 由S△ABC＝S△ABP＋S△APC ‎＝×x×3＋×y× ＝(3x＋y)． ① …… 4分 因为tana＝－2，所以sina＝． ‎ 所以S△ABC＝×x×y× ． ② ……………………………………… 8分 由①②可得×x×y× ＝(3x＋y)．‎ 即3x＋5y＝2xy． ③ ………………………………………10分 因为3x＋5y≥2，所以 2xy≥2．‎ 解得xy≥15． ………………………………………13分 当且仅当3x＝5y取“＝”，结合③解得x＝5，y＝3． ‎ 所以S△ABC＝×x×y× 有最小值15．‎ 答：当AB＝‎5km时，该工业园区的面积最小，最小面积为‎15km2．……………… 15分 ‎19．（本小题满分16分）‎ 解：（1）当a＝－1，x[0，＋∞)时，f(x)＝－x3＋x＋1，从而f ′(x)＝－3x2＋1．‎ 当x＝1时，f(1)＝1，f ′(1)＝－2，‎ 所以函数y＝f(x) (x[0，＋∞))的图象在x＝1处的切线方程为y－1＝－2(x－1)，‎ 即2x＋y－3＝0． ………………………………………………… 3分 ‎（2）f(x)＝g(x)即为ax3＋|x－a|＝x4．‎ 所以x4－ax3＝|x－a|，从而x3(x－a)＝|x－a|．‎ 此方程等价于x＝a或或 ………………………………………… 6分 所以当a≥1时，方程f(x)＝g(x)有两个不同的解a，－1；‎ 当－1＜a＜1时，方程f(x)＝g(x)有三个不同的解a，－1，1；‎ 当a≤－1时，方程f(x)＝g(x)有两个不同的解a，1． …………………………… 9‎ 分 ‎（3）当a＞0，x(a，＋∞)时，f(x)＝ax3＋x－a，f ′(x)＝3ax2＋1＞0，‎ 所以函数f(x)在(a，＋∞)上是增函数，且f(x)＞f(a)＝a4＞0．‎ 所以当x[a，a＋2]时，f(x)[f(a)，f(a＋2)]，[，]，‎ 当x[a＋2，＋∞)时，f(x)[ f(a＋2)，＋∞)． …………………………………… 11分 因为对任意的x1[a，a＋2]，都存在x2[a＋2，＋∞)，使得f(x1)f(x2)＝1024，‎ 所以[，][ f(a＋2)，＋∞)． ………………………………………… 13分 从而≥f(a＋2)．‎ 所以f 2(a＋2)≤1024，即f(a＋2)≤32，也即a(a＋2)3＋2≤32．‎ 因为a＞0，显然a＝1满足，而a≥2时，均不满足．‎ 所以满足条件的正整数a的取值的集合为{1}． …………………………………… 16分 ‎20．解：（1）由(Sm＋n＋S1)2＝‎4a2na‎2m，得(S2＋S1)2＝‎4a，即(a2＋‎2a1)2＝‎4a．‎ 因为a1＞0，a2＞0，所以a2＋‎2a1＝a2，即＝2． ………………………… 3分 证明：（2）（方法一）令m＝1，n＝2，得(S3＋S1)2＝‎4a2a4，即(‎2a1＋a2＋a3)2＝‎4a2a4，‎ 令m＝n＝2，得S4＋S1＝‎2a4，即‎2a1＋a2＋a3＝a4．‎ 所以a4＝‎4a2＝‎8a1．‎ 又因为＝2，所以a3＝‎4a1． ………………………… 6分 由(Sm＋n＋S1)2＝‎4a2na‎2m，得(Sn＋1＋S1)2＝‎4a2na2，(Sn＋2＋S1)2＝‎4a2na4．‎ 两式相除，得＝，所以＝＝2．‎ 即Sn＋2＋S1＝2(Sn＋1＋S1)，‎ 从而Sn＋3＋S1＝2(Sn＋2＋S1)．‎ 所以an＋3＝2an＋2，故当n≥3时，{an}是公比为2的等比数列．‎ 又因为a3＝‎2a2＝‎4a1，从而an＝a1·2 n－1，n∈N*．‎ 显然，an＝a1·2 n－1满足题设，‎ 因此{an}是首项为a1，公比为2的等比数列． ………………………… 10分 ‎（方法二）在(Sm＋n＋S1)2＝‎4a2na‎2m中，‎ 令m＝n，得S2n＋S1＝‎2a2n． ①‎ 令m＝n＋1，得S2n＋1＋S1＝2 ， ②‎ 在①中，用n＋1代n得，S2n＋2＋S1＝‎2a2n＋2． ③‎ ‎②－①，得a2n＋1＝2－‎2a2n＝2(－)， ④‎ ‎③－②，得a2n＋2＝‎2a2n＋2－2＝2(－)， ⑤‎ 由④⑤得a2n＋1＝． ⑥‎ ‎………………………… 8分 ‎⑥代入④，得a2n＋1＝‎2a2n；⑥代入⑤得a2n＋2＝‎2a2n＋1，‎ 所以＝＝2．又＝2，‎ 从而an＝a1·2 n－1，n∈N*．‎ 显然，an＝a1·2 n－1满足题设，‎ 因此{an}是首项为a1，公比为2的等比数列． ………………………… 10分 ‎（3）由（2）知，an＝a1·2 n－1．‎ 因为|cp|＝|dp|＝a1·2p－1，所以cp＝dp或cp＝－dp．‎ 若cp＝－dp，不妨设cp＞0，dp＜0，‎ 则Tp≥a1·2p－1－(a1·2p－2＋a1·2p－3＋…＋a1)＝a1·2p－1－a1·(2p－1－1)＝a1＞0．‎ Rp≤－a1·2p－1＋(a1·2p－2＋a1·2p－3＋…＋a1)＝－a1·2p－1＋a1·(2p－1－1)＝－a1＜0．‎ 这与Tp＝Rp矛盾，所以cp＝dp．‎ 从而Tp－1＝Rp－1．‎ 由上证明，同理可得cp－1＝dp－1．如此下去，可得cp－2＝dp－2，cp－3＝dp－3．…，c1＝d1．‎ 即对任意正整数k(1≤k≤p)，ck＝dk． ………………………… 16分