2017-2018学年陕西省黄陵中学高新部高二下学期开学考试数学理试题（解析版） 14页

‎2017-2018学年陕西省黄陵中学高新部高二下学期开学考试数学理试题（解析版）‎ 一、选择题(本大题共12个小题，每小题5分，共60分。) ‎ ‎1. 已知为正数，则“”是“ ”的 （ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎【答案】C ‎【解析】设，则在上单调递减。‎ 若，则，即；‎ 若，即，则有。‎ 综上可得“”是“ ”的充要条件。‎ 选C。‎ ‎2. 由命题“存在，使”是假命题，得m的取值范围是，则实数a的值是（ ）‎ A. 2 B. C. 1 D. ‎ ‎【答案】C ‎【解析】由题意命题“存在，使”是假命题 ∴对于任意的都成立，即 恒成立． 又 ．所以. 故选C.‎ ‎3. 如图，空间四边形中，点分别在上， ， ，则 ( )‎ A. B. ‎ C. D. 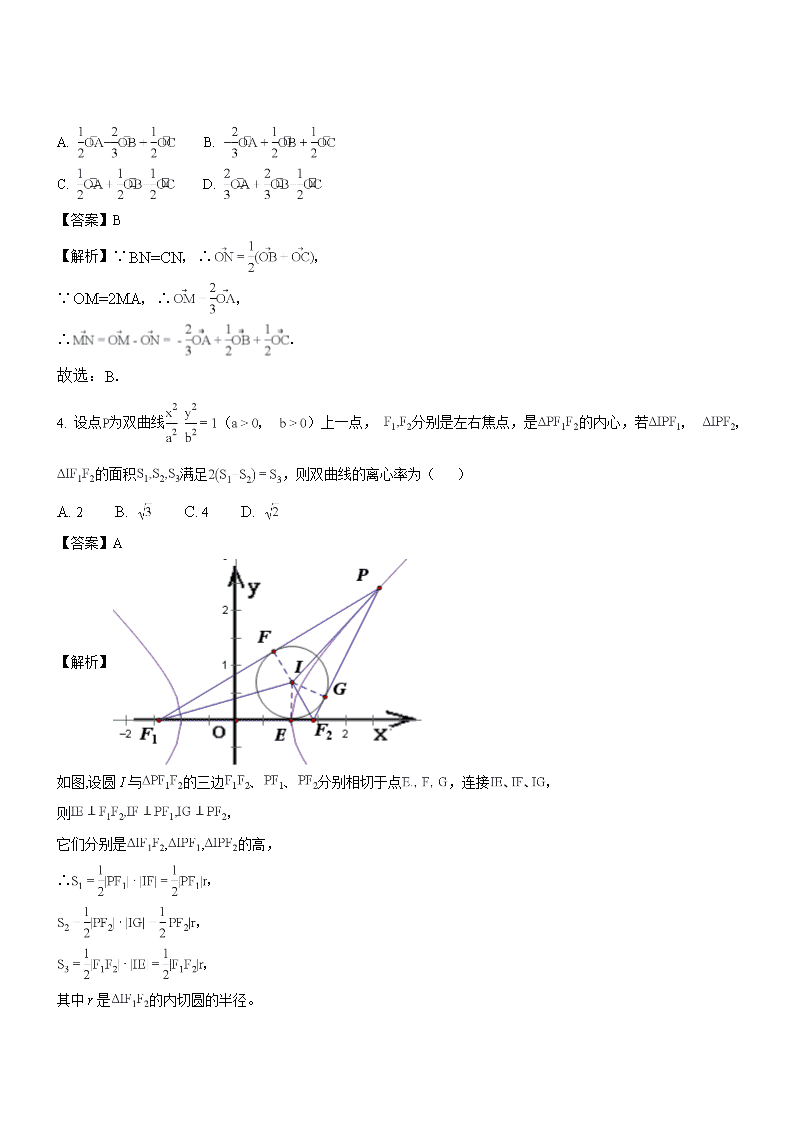‎ ‎【答案】B ‎【解析】∵BN=CN，∴，‎ ‎∵OM=2MA，∴，‎ ‎∴．‎ 故选：B．‎ ‎4. 设点为双曲线（， ）上一点， 分别是左右焦点，是的内心，若， ， 的面积满足，则双曲线的离心率为（ ）‎ A. 2 B. C. 4 D. ‎ ‎【答案】A ‎【解析】‎ 如图,设圆I与的三边、、分别相切于点，连接，‎ 则，‎ 它们分别是,,的高，‎ ‎∴，‎ ‎，‎ ‎，‎ 其中r是的内切圆的半径。‎ ‎∵，‎ ‎∴− =，‎ 两边约去r得：，‎ 根据双曲线定义,得，‎ ‎∴离心率为.‎ 故选：A.‎ ‎5. 椭圆的左、右顶点分别是A、B，左、右焦点分别是F1，F2．若，，成等比数列，则此椭圆的离心率为(　　)‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】∵椭圆的左、右顶点分别是，左、右焦点分别是 设椭圆的半焦距为， 则 成等比数列， 即 ‎ 故选A．‎ ‎6. 若两点,，当||取最小值时，的值等于(　　)‎ A. 19 B. C. D. ‎ ‎【答案】B ‎【解析】∵,， ， ‎ ‎∴当|取最小值时的值等于． 故选C．‎ ‎7. 已知命题p:∃ ，,命题q: ,则(　　)‎ A. 命题p∨q是假命题 B. 命题p∧q是真命题 C. 命题p∧()是真命题 D. 命题p∨()是假命题 ‎【答案】C ‎【解析】命题p:∃ ，为真命题；,命题q: 为假命题，‎ 故命题p∧()是真命题.‎ 故选C.‎ ‎8. 设F1，F2为曲线C1：的焦点，P是曲线C2：与C1的一个交点，则cos∠F1PF2的值是(　　)‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】依题意，曲：的焦点为 双曲线：的焦点也为 是曲线与的一个交点，设其为第一象限的点 由椭圆与双曲线定义可知 解得 ‎ 设 则 ‎ 故选C．‎ ‎【点睛】本题综合考查了椭圆与双曲线的定义，解题时要透过现象看本质，用联系的观点解题．‎ ‎9. 已知，分别为双曲线的左，右焦点，点在双曲线上.若，则的面积为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】不妨设点在双曲线的右支上，令，‎ 由双曲线的定义有：，①‎ 在中，由余弦定理有：，‎ 即：，②‎ ‎①-②可得：，则的面积为.‎ 本题选择B选项.‎ 点睛：双曲线上一点与两焦点构成的三角形，称为双曲线的焦点三角形，与焦点三角形有关的计算或证明常利用正弦定理、余弦定理、||PF1|-|PF2||＝2a，得到a，c的关系．‎ ‎10. 过抛物线 的焦点作倾斜角为的直线，交抛物线于、两点，则（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】设过抛物线的焦点且倾斜角为的直线方程为，且与抛物线交于点，联立，‎ 得，则，则或；故选C.‎ 点睛：本题考查直线和抛物线的位置关系；再处理直线与抛物线的位置关系时，往往设直线方程为的形式，这样可以避免讨论直线无斜率的情况，且联立方程组、整理方程时的运算量较小.‎ ‎11. 由直线上的一点向圆引切线，则切线长的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】设圆心为，直线上点为，切点为，‎ 由题意可得：，‎ 切线长最小时最小即可，‎ 利用点到直线距离公式可得：，‎ 则切线长的最小值为.‎ 本题选择C选项.‎ ‎12. 2016年1月14日，国防科工局宣布，嫦娥四号任务已经通过了探月工程重大专项领导小组审议通过，正式开始实施，如图所示，假设“嫦娥四号”卫星将沿地月转移轨道飞向月球后，在月球附近一点变轨进入月球球为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在点第二次变轨进入仍以为一个焦点的椭圆轨道Ⅱ绕月飞行，若用和分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用和分别表示椭圆轨道Ⅰ和Ⅱ的长轴长，给出下列式子：① ② ③ ④‎ 其中正确的式子的序号是（ ）‎ A. ②③ B. ①④ C. ①③ D. ②④‎ ‎【答案】B ‎【解析】因为，所以，即①正确，由图可得，所以，即②错误；由，得，即，即，即，即③错误，且，即④正确；故选B.‎ 二、填空题：(本大题共4小题，每小题5分，共20分，将答案填在答题纸的横线上）‎ ‎13. 对四个样本点，，，分析后，得到回归直线方程为，则样本点中的值为__________．‎ ‎【答案】7.01‎ ‎【解析】由回归直线一定过样本中心点可得：‎ ‎14. 若在上是减函数，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】试题分析：转化为在上恒成立，即在上恒成立，令 ‎，所以，则的取值范围是.‎ 考点：1.导数判断函数的单调性；2.不等式恒成立.‎ ‎15. 在区间内任取两个实数，则这两个实数的和大于的概率为__________．‎ ‎【答案】‎ ‎16. 对于三次函数 ，给出定义：设是的导数，是的导数，若方程有实数解，则称点为函数的“拐点”.某同学经过探究发现：任何一个三次函数都有“拐点”，任何一个三次函数都有对称中心，且“拐点”就是对称中心.设函数，则 __________．‎ ‎【答案】2017‎ ‎【解析】由题可得：，所以对称中心为（，） ，设g(x)上任意一点，因为关于（，）对称，所以P关于其对称的对称点为在g(x)上，且所以，故 2017‎ 二、解答题（本大题共6小题，共70分。请在答题纸指定区域内作答，解答时应写出文字说明、证明过程或演算步骤。）‎ ‎17. (1)设.‎ ‎①求；‎ ‎②求；‎ ‎③求；‎ ‎(2)求除以9的余数．‎ ‎【答案】（1）16，256，15；（2）7‎ ‎【解析】试题分析：（1）利用赋值法，令，求；（2）令x=-1，与（2）相加求；，； ③令，结合二项式系数和即可求出结果； （2）利用二项式系数和，把 分解为9的倍数形式，再求对应的余数．‎ 试题解析：(1)①令x＝1，得a0＋a1＋a2＋a3＋a4＝(3－1)4＝16. ‎ ‎②令x＝－1得，a0－a1＋a2－a3＋a4＝(－3－1)4＝256，‎ 而由(1)知a0＋a1＋a2＋a3＋a4＝(3－1)4＝16，两式相加，得a0＋a2＋a4＝136. ‎ ‎③令x＝0得a0＝(0－1)4＝1，得a1＋a2＋a3＋a4＝a0＋a1＋a2＋a3＋a4－a0＝16－1＝15.‎ ‎（2）解　S＝C＋C＋…＋C＝227－1‎ ‎＝89－1＝(9－1)9－1＝C×99－C×98＋…＋C×9－C－1‎ ‎＝9(C×98－C×97＋…＋C)－2‎ ‎＝9(C×98－C×97＋…＋C－1)＋7，‎ 显然上式括号内的数是正整数．‎ 故S被9除的余数为7.‎ ‎18. 如图是大丰区新丰中学2016年校园“十佳歌手”大奖赛上，七位评委为甲、乙两位选手打出的分数的茎叶图.‎ ‎（1）写出评委为乙选手打出分数数据的众数，中位数；‎ ‎（2）求去掉一个最高分和一个最低分后，两位选手所剩数据的平均数和方差，根据结果比较，哪位选手的数据波动小？‎ ‎【答案】（1）84，84；（2）乙的数据波动小 ‎【解析】试题分析：（1）根据茎叶图及数据特点，众数为出现频数多的数，中位数为从小到大排处于中间位置的数,显然乙选手打出分数的众数为，中位数；（2）在甲乙中分别去掉一个最高分和一个最低分之后，得到，根据结果方差越大越不稳定，显然乙的数据波动小.‎ 试题解析：（1）众数为，中位数；‎ ‎（2），所以，所以乙的数据波动小.‎ 考点：1.茎叶图；2.众数，中位数，平均数和方差.‎ ‎19. 在如图所示的几何体中，四边形为矩形，平面平面，//,,,点在棱上. ‎ ‎（1）求证：；‎ ‎（2）若是的中点，求异面直线与所成角的余弦值；‎ ‎（3）是否存在正实数，使得，且满足二面角的余弦值为，若存在，求出的值，若不存在，请说明理由.‎ ‎【答案】（1）见解析；（2）；（3）2‎ ‎【解析】试题分析：（1）利用面面垂直的性质定理、线面垂直的判定定理及其性质定理即可得出． （2）以为坐标原点，分别为轴建立如图所示空间直角坐标系．‎ 求得，利用平面法向量的夹角公式即可得出异面直线与所成角的余弦值；‎ ‎（3）假设存在正实数满足题意，易知平面的一个法向量为，设，‎ 由，求得，进而求得，，求得平面的一个法向量为，利用平面法向量的夹角公式即可得出．‎ 试题解析：(1)证：平面平面，‎ ‎ 平面平面，‎ ‎ ‎ 又 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 又四边形为矩形，‎ 以为坐标原点，分别为轴建立如图所示空间直角坐标系.则，‎ ‎ ，，则 ‎，，‎ ‎ ‎ ‎ 异面直线所成角的余弦值为 ‎（3）假设存在正实数满足题意，易知平面的一个法向量为，设，‎ 由得：得：‎ ‎ 即： ‎ ‎，‎ 设平面的一个法向量为则 ‎ 即 令，则，‎ 即 ， 则 解之得：‎ 综上所述，存在满足题意.‎ ‎20. 已知函数f（x）=x2+（lga+2）x+lgb满足f（﹣1）=﹣2且对于任意x∈R，恒有f（x）≥2x成立．‎ ‎（1）求实数a，b的值；‎ ‎（2）解不等式f（x）＜x+5．‎ ‎【答案】（1）100；（2）‎ ‎【解析】试题分析：（1）由，代入函数解析式得到化简后得到关于 的等式记作②，又因为恒成立，把的解析式代入后，令0，根据平方大于等于0，即可求出 的值，把的值代入②即可求出的值； （2）由（1）可确定出的解析式，然后解关于的一元二次不等式即可．‎ 试题解析：（1）由f（﹣1）=﹣2知，lgb﹣lga+1=0①，所以②．‎ 又f（x）≥2x恒成立，f（x）﹣2x≥0恒成立，‎ 则有x2+x•lga+lgb≥0恒成立，‎ 故△=（lga）2﹣4lgb≤0，‎ 将①式代入上式得：（lgb）2﹣2lgb+1≤0，即（lgb﹣1）2≤0，‎ 故lgb=1即b=10，代入②得，a=100；‎ ‎（2）由（1）知f（x）=x2+4x+1，f（x）＜x+5，‎ 即x2+4x+1＜x+5，‎ 所以x2+3x﹣4＜0，‎ 解得﹣4＜x＜1，‎ 因此不等式的解集为{x|﹣4＜x＜1}．‎ ‎21. 已知函数 ‎（1）若函数在处取得极值，求的值；‎ ‎（2）若函数的图象上存在两点关于原点对称，求的取值范围.‎ ‎【答案】（1）；（2）‎ ‎【解析】试题分析：（1）当时，.从而，解出即可，（2）由题意得到方程组，求出的表达式，设，再通过求导求出函数的最小值，问题得以解决．‎ 试题解析：（1）当时，.‎ 因为在处取得极值，所以，即 ‎，解得，经验证满足题意，所以.‎ ‎(2)由题意知的图像上存在两点关于原点对称，即 图象上存在一点，使得 在的图象上，即有 ‎ 消去，得 ‎ ，化简得.‎ 则由题意关于的方程在上有解.‎ 设，‎ 令，得，当时，，在为增函数；‎ 当时，，在为减函数.‎ 所以 ‎，即的值域为.‎ 所以当时，方程在上有解.‎ 所以当时，函数的图像上存在两点关于原点对称.‎ ‎22. 已知函数.‎ ‎（1）求函数的单调区间和最小值；‎ ‎（2）若函数在上的最小值为，求的值；‎ ‎（3）若,且对任意恒成立，求的最大值.‎ ‎【答案】（1）见解析；（2）见解析；（3）3‎ ‎【解析】试题分析：（1）求导函数，由导数的正负，可得函数的单调区间； （2），对结合在上的最小值为，分类讨论，建立等式，从而可得结论．‎ ‎（3）问题转化为对任意恒成立，设，根据函数的单调性求出的值即可．‎ 试题解析：（1）的单调增区间为，单调减区间为，‎ ‎（2），，‎ Ⅰ．当时，，在上单调递增，，所以，舍去.‎ Ⅱ．当时，在上单调递减，在上单调递增，‎ ‎①若，在上单调递增，，所以，舍去，‎ ‎②若，在上单调递减，在上单调递增，所以，解得.‎ ‎③若，在上单调递减，，所以，舍去，‎ 综上所述，.‎ ‎（3）由题意得：对任意恒成立，即对任意恒成立.‎ 令，则，令，则，‎ 所以函数在上单调递增，‎ 因为方程在上存在唯一的实根，且，当时，，即，‎ 当时，，即.‎ 所以函数在上递减，在上单调递增.‎ 所以 所以，又因为，故整数的最大值为3.‎ ‎【点睛】本题考查导数知识的运用，考查函数的单调性，考查函数的最值以及恒成立问题，考查分类讨论的数学思想，正确分类是关键