【数学】2018届一轮复习人教A版第十章计数原理、概率第6讲离散型随机变量及其分布列课时作业 7页

第6讲　离散型随机变量及其分布列 基础巩固题组 ‎(建议用时：40分钟)‎ 一、选择题 ‎1.某射手射击所得环数X的分布列为 X ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ P ‎0.02‎ ‎0.04‎ ‎0.06‎ ‎0.09‎ ‎0.28‎ ‎0.29‎ ‎0.22‎ 则此射手“射击一次命中环数大于‎7”‎的概率为(　　)‎ A.0.28‎‎ B.‎0.88 C.0.79 D.0.51‎ 解析　P(X＞7)＝P(X＝8)＋P(X＝9)＋P(X＝10)＝0.28＋0.29＋0.22＝0.79.‎ 答案　C ‎2.设X是一个离散型随机变量，其分布列为：‎ X ‎－1‎ ‎0‎ ‎1‎ P ‎2－3q q2‎ 则q的值为(　　)‎ A.1 B.± C.－ D.＋ 解析　由分布列的性质知 解得q＝－.‎ 答案　C ‎3.设某项试验的成功率是失败率的2倍，用随机变量X去描述1次试验的成功次数，则P(X＝0)等于(　　)‎ A.0 B. C. D. 解析　由已知得X的所有可能取值为0，1，‎ 且P(X＝1)＝2P(X＝0)，由P(X＝1)＋P(X＝0)＝1，‎ 得P(X＝0)＝.‎ 答案　C ‎4.在15个村庄中有7个村庄交通不方便，现从中任意选10个村庄，用X表示这10个村庄中交通不方便的村庄数，下列概率中等于的是(　　)‎ A.P(X＝2) B.P(X≤2)‎ C.P(X＝4) D.P(X≤4)‎ 解析　X服从超几何分布P(X＝k)＝，故k＝4.‎ 答案　C ‎5.从装有3个白球、4个红球的箱子中，随机取出了3个球，恰好是2个白球、1个红球的概率是(　　)‎ A. B. C. D. 解析　如果将白球视为合格品，红球视为不合格品，则这是一个超几何分布问题，故所求概率为P＝＝.‎ 答案　C 二、填空题 ‎6.(2017·金华调研)设离散型随机变量X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ P ‎0.2‎ ‎0.1‎ ‎0.1‎ ‎0.3‎ m ‎(1)则m＝________；‎ ‎(2)若随机变量Y＝|X－2|，则P(Y＝2)＝________.‎ 解析　由分布列的性质，知 ‎0.2＋0.1＋0.1＋0.3＋m＝1，∴m＝0.3.‎ 由Y＝2，即|X－2|＝2，得X＝4或X＝0，‎ ‎∴P(Y＝2)＝P(X＝4或X＝0)‎ ‎＝P(X＝4)＋P(X＝0)‎ ‎＝0.3＋0.2＝0.5.‎ 答案　(1)0.3　(2)0.5‎ ‎7.袋中有4只红球3只黑球，从袋中任取4只球，取到1只红球得1分，取到1只黑球得3分，设得分为随机变量X，则P(X≤6)＝________.‎ 解析　P(X≤6)＝P(取到3只红球1只黑球)＋P(取到4只红球)＝＋＝.‎ 答案　 ‎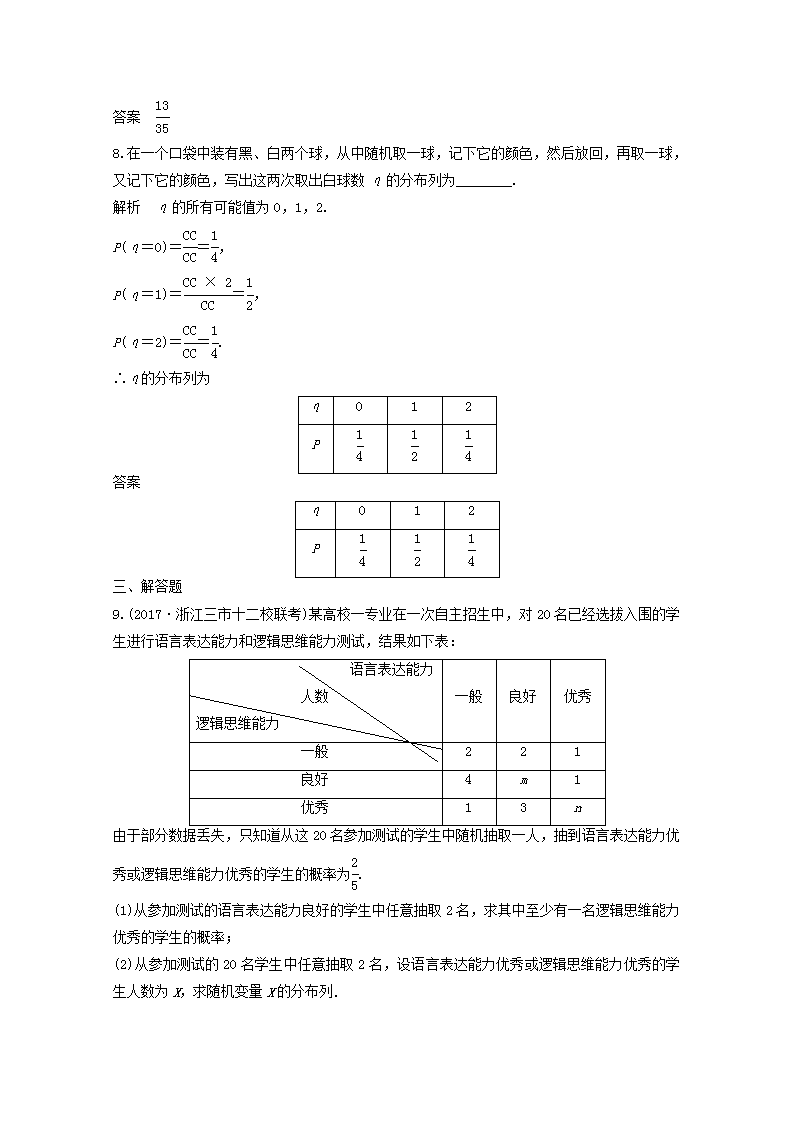8.在一个口袋中装有黑、白两个球，从中随机取一球，记下它的颜色，然后放回，再取一球，‎ 又记下它的颜色，写出这两次取出白球数η的分布列为________.‎ 解析　η的所有可能值为0，1，2.‎ P(η＝0)＝＝，‎ P(η＝1)＝＝，‎ P(η＝2)＝＝.‎ ‎∴η的分布列为 η ‎0‎ ‎1‎ ‎2‎ P 答案　‎ η ‎0‎ ‎1‎ ‎2‎ P 三、解答题 ‎9.(2017·浙江三市十二校联考)某高校一专业在一次自主招生中，对20名已经选拔入围的学生进行语言表达能力和逻辑思维能力测试，结果如下表：‎ 语言表达能力 人数 逻辑思维能力 一般 良好 优秀 一般 ‎2‎ ‎2‎ ‎1‎ 良好 ‎4‎ m ‎1‎ 优秀 ‎1‎ ‎3‎ n 由于部分数据丢失，只知道从这20名参加测试的学生中随机抽取一人，抽到语言表达能力优秀或逻辑思维能力优秀的学生的概率为.‎ ‎(1)从参加测试的语言表达能力良好的学生中任意抽取2名，求其中至少有一名逻辑思维能力优秀的学生的概率；‎ ‎(2)从参加测试的20名学生中任意抽取2名，设语言表达能力优秀或逻辑思维能力优秀的学生人数为X，求随机变量X的分布列.‎ 解　(1)用A表示“从这20名参加测试的学生中随机抽取一人，抽到语言表达能力优秀或逻辑思维能力优秀的学生”，‎ ‎∵语言表达能力优秀或逻辑思维能力优秀的学生共有(6＋n)名，‎ ‎∴P(A)＝＝，解得n＝2，∴m＝4，‎ 用B表示“从参加测试的语言表达能力良好的学生中任意抽取2名，其中至少有一名逻辑思维能力优秀的学生”，‎ ‎∴P(B)＝1－＝.‎ ‎(2)随机变量X的可能取值为0，1，2.‎ ‎∵20名学生中，语言表达能力优秀或逻辑思维能力优秀的学生人数共有8名，‎ ‎∴P(X＝0)＝＝，‎ P(X＝1)＝＝，‎ P(X＝2)＝＝，‎ ‎∴X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P ‎10.某超市在节日期间进行有奖促销，凡在该超市购物满300元的顾客，将获得一次摸奖机会，规则如下：‎ 奖盒中放有除颜色外完全相同的1个红球，1个黄球，1个白球和1个黑球.顾客不放回地每次摸出1个球，若摸到黑球则停止摸奖，否则就要将奖盒中的球全部摸出才停止.规定摸到红球奖励10元，摸到白球或黄球奖励5元，摸到黑球不奖励.‎ ‎(1)求1名顾客摸球3次停止摸奖的概率；‎ ‎(2)记X为1名顾客摸奖获得的奖金数额，随机变量X的分布列.‎ 解　(1)设“1名顾客摸球3次停止摸奖”为事件A，‎ 则P(A)＝＝，‎ 故1名顾客摸球3次停止摸球的概率为.‎ ‎(2)随机变量X的所有取值为0，5，10，15，20.‎ P(X＝0)＝，P(X＝5)＝＝，‎ P(X＝10)＝＋＝，P(X＝15)＝＝，‎ P(X＝20)＝＝.‎ 所以，随机变量X的分布列为 X ‎0‎ ‎5‎ ‎10‎ ‎15‎ ‎20‎ P 能力提升题组 ‎(建议用时：25分钟)‎ ‎11.随机变量X的分布列如下：‎ X ‎－1‎ ‎0‎ ‎1‎ P a b c 其中a，b，c成等差数列，则P(|X|＝1)等于(　　)‎ A. B. C. D. 解析　∵a，b，c成等差数列，∴2b＝a＋c.又a＋b＋c＝1，∴b＝，∴P(|X|＝1)＝a＋c＝.‎ 答案　D ‎12.随机变量X的概率分布规律为P(X＝n)＝(n＝1，2，3，4)，其中a是常数，则P的值为(　　)‎ A. B. C. D. 解析　因为P(X＝n)＝(n＝1，2，3，4)，‎ 所以＋＋＋＝a＝1.∴a＝，‎ 故P＝P(X＝1)＋P(X＝2)＝×＋×＝.‎ 答案　D ‎13.(2017·石家庄调研)为检测某产品的质量，现抽取5件产品，测量产品中微量元素x，y的含量(单位：毫克)，测量数据如下：‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ x ‎169‎ ‎178‎ ‎166‎ ‎175‎ ‎180‎ y ‎75‎ ‎80‎ ‎77‎ ‎70‎ ‎81‎ 如果产品中的微量元素x，y满足x≥175且y≥75时，该产品为优等品.‎ 现从上述5件产品中，随机抽取2件，则抽取的2件产品中优等品数X的分布列为________.‎ 解析　5件抽测品中有2件优等品，则X的可能取值为0，1，2.P(X＝0)＝＝0.3，‎ P(X＝1)＝＝0.6，‎ P(X＝2)＝＝0.1.‎ ‎∴优等品数X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P ‎0.3‎ ‎0.6‎ ‎0.1‎ 答案　‎ X ‎0‎ ‎1‎ ‎2‎ P ‎0.3‎ ‎0.6‎ ‎0.1‎ ‎14.盒内有大小相同的9个球，其中2个红色球，3个白色球，4个黑色球.规定取出1个红色球得1分，取出1个白色球得0分，取出1个黑色球得－1分.现从盒内任取3个球.‎ ‎(1)求取出的3个球中至少有1个红球的概率；‎ ‎(2)求取出的3个球得分之和恰为1分的概率；‎ ‎(3)设X为取出的3个球中白色球的个数，求X的分布列.‎ 解　(1)P＝1－＝.‎ ‎(2)记“取出1个红色球，2个白色球”为事件B，“取出2个红色球，1个黑色球”为事件C，则P(B＋C)＝P(B)＋P(C)＝＋＝.‎ ‎(3)X可能的取值为0，1，2，3，X服从超几何分布，所以 P(X＝k)＝，k＝0，1，2，3.‎ 故P(X＝0)＝＝，P(X＝1)＝＝，‎ P(X＝2)＝＝，P(X＝3)＝＝.‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎15.(2017·温州调研)在一个盒子中，放有标号分别为1，2，3的三张卡片，现从这个盒子中，有放回地先后抽得两张卡片的标号分别为x，y，记X＝|x－2|＋|y－x|.‎ ‎(1)求随机变量X的最大值，并求事件“X取得最大值”的概率；‎ ‎(2)求随机变量X的分布列.‎ 解　(1)由题意知，x，y可能的取值为1，2，3，‎ 则|x－2|≤1，|y－x|≤2，‎ 所以X≤3，且当x＝1，y＝3或x＝3，y＝1时，X＝3.‎ 因此，随机变量X的最大值为3.‎ 而有放回地抽两张卡片的所有情况有3×3＝9(种)，‎ 所以P(X＝3)＝.故随机变量X的最大值为3，事件“X取得最大值”的概率为.‎ ‎(2)X的所有取值为0，1，2，3.‎ 当X＝0时，只有x＝2，y＝2这一种情况，‎ 当X＝1时，有x＝1，y＝1或x＝2，y＝1或x＝2，y＝3或x＝3，y＝3四种情况，‎ 当X＝2时，有x＝1，y＝2或x＝3，y＝2两种情况.‎ 当X＝3时，有x＝1，y＝3或x＝3，y＝1两种情况.‎ 所以P(X＝0)＝，P(X＝1)＝，P(X＝2)＝，‎ P(X＝3)＝.‎ 则随机变量X的分布列为 X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P