2021版新高考数学一轮复习单元质检卷四三角函数解三角形B新人教A版 1 10页

单元质检卷四　三角函数、解三角形(B)‎ ‎(时间:45分钟　满分:100分)‎ 一、单项选择题(本大题共4小题,每小题7分,共28分)‎ ‎1.(2019广东珠海二模)已知tan α=-2,其中α为三角形内角,则cos α=(　　)‎ A.-‎5‎‎5‎ B.‎‎2‎‎5‎‎5‎ C.‎5‎‎5‎ D.-‎‎2‎‎5‎‎5‎ ‎2.已知函数f(x)=‎1‎‎2‎sin 2x+‎3‎‎2‎cos 2x,把函数f(x)的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把所得到的曲线向左平移π‎6‎个单位长度,得到函数g(x)的图象,则函数g(x)的对称中心是(　　)‎ A.‎2kπ+π‎6‎,0‎,k∈Z B.‎2kπ+π‎2‎,0‎,k∈Z C.kπ+π‎2‎,0‎,k∈Z D.kπ+π‎4‎,0‎,k∈Z ‎3.在△ABC中,内角A,B,C所对的边分别为a,b,c,∠ABC=120°,∠ABC的平分线交AC于点D,且BD=1,则4a+c的最小值为(　　)‎ A.8 B.9 C.10 D.7‎ ‎4.如图,函数y=|tan x|cos x0≤x<‎3π‎2‎,x≠π‎2‎的图象是(　　)‎ 10‎ 二、多项选择题(本大题共2小题,每小题7分,共14分)‎ ‎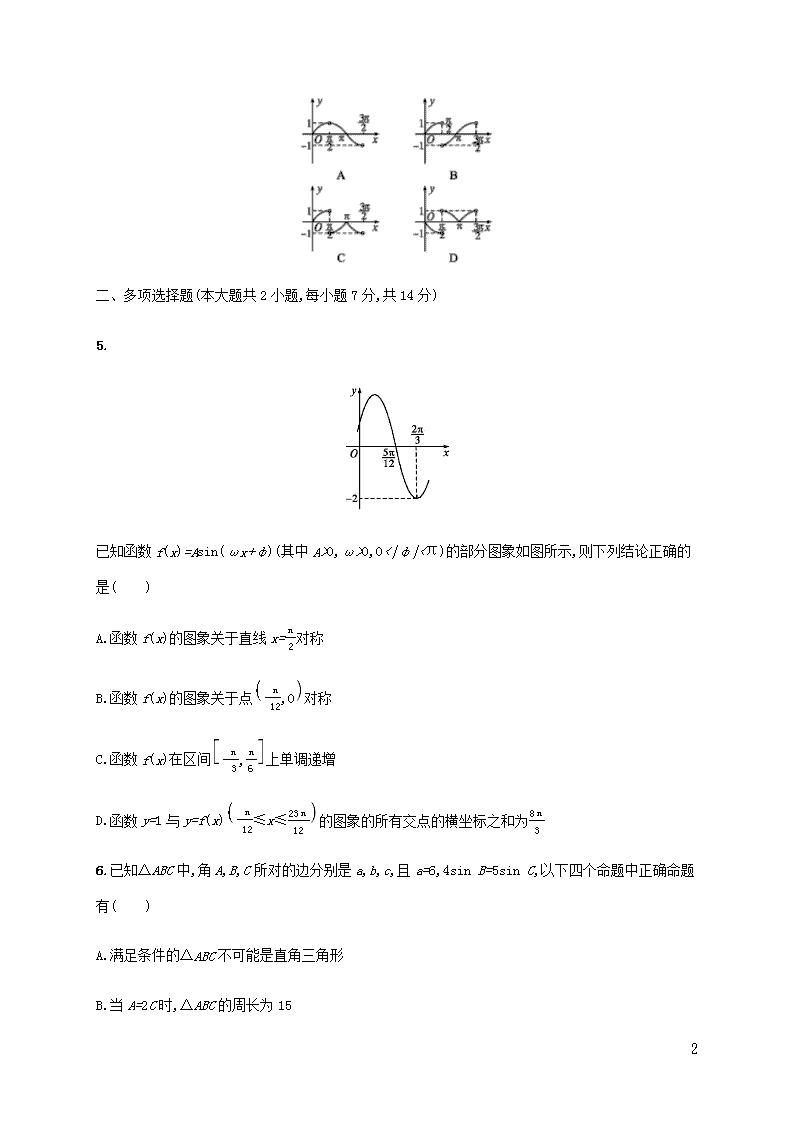5.‎ 已知函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<|φ|<π)的部分图象如图所示,则下列结论正确的是(　　)‎ A.函数f(x)的图象关于直线x=π‎2‎对称 B.函数f(x)的图象关于点-π‎12‎,0对称 C.函数f(x)在区间-π‎3‎‎,‎π‎6‎上单调递增 D.函数y=1与y=f(x)-π‎12‎≤x≤‎23π‎12‎的图象的所有交点的横坐标之和为‎8π‎3‎ ‎6.已知△ABC中,角A,B,C所对的边分别是a,b,c,且a=6,4sin B=5sin C,以下四个命题中正确命题有(　　)‎ A.满足条件的△ABC不可能是直角三角形 B.当A=2C时,△ABC的周长为15‎ 10‎ C.当A=2C时,若O为△ABC的内心,则△AOB的面积为‎7‎ D.△ABC的面积的最大值为40‎ 三、填空题(本大题共2小题,每小题7分,共14分)‎ ‎7.已知△ABC是锐角三角形,a,b,c分别是A,B,C的对边.若A=2B,则 ‎(1)角B的取值范围是　　　　　　. ‎ ‎(2)ab‎+‎ba的取值范围是　　　　　　. ‎ ‎8.已知实数a>0,若函数f(x)=a(sin x+cos x)-sin xcos x(x∈R)的最大值为‎9‎‎2‎,则a的值为　　　　. ‎ 四、解答题(本大题共3小题,共44分)‎ ‎9.(14分)(2019重庆渝中区一模)在△ABC中,内角A,B,C所对的边分别为a,b,c,2acos C=b.‎ ‎(1)证明:A=C;‎ ‎(2)若B为钝角,△ABC的面积为‎2‎‎3‎a2,求ba.‎ ‎10.(15分)△ABC的内角A,B,C的对边分别为a,b,c.已知△ABC的面积为a‎2‎‎3sinA.‎ 10‎ ‎(1)求sin Bsin C;‎ ‎(2)若6cos Bcos C=1,a=3,求△ABC的周长.‎ ‎11.(15分)(2019山东济南一中期末)已知向量a=cos‎3‎‎2‎x,sin‎3‎‎2‎x,b=cosx‎2‎,sinx‎2‎,且x∈-‎2π‎3‎‎,‎π‎2‎.‎ ‎(1)当x=π‎3‎时,求a·b及|a+b|的值;‎ ‎(2)若函数f(x)=a·b-2λ|a+b|的最小值是-1,求实数λ的值.‎ 参考答案 单元质检卷四　三角函数、‎ 解三角形(B)‎ ‎1.A　∵tanα=-2<0,‎∴‎π‎2‎<α<π,‎ 10‎ 则sinα=-2cosα,‎ 代入sin2α+cos2α=1得cos2α=‎1‎‎5‎,则cosα=-‎5‎‎5‎,故选A.‎ ‎2.C　函数f(x)=‎1‎‎2‎sin2x+‎3‎‎2‎cos2x=sin‎2x+‎π‎3‎‎.‎由题意,得g(x)=sinx+π‎2‎=cosx,所以函数g(x)的对称中心是kπ+π‎2‎,0‎,k∈Z.‎ ‎3.B　由题意得‎1‎‎2‎acsin120°=‎1‎‎2‎asin60°+‎1‎‎2‎csin60°,即ac=a+c,得‎1‎a‎+‎‎1‎c=1,‎ 得4a+c=(4a+c)‎1‎a‎+‎‎1‎c=ca‎+‎‎4ac+5≥2ca‎·‎‎4ac+5=4+5=9,‎ 当且仅当ca‎=‎‎4ac,即c=2a时,取等号,故选B.‎ ‎4.C　∵y=|tanx|cosx=‎sinx,x∈[0,π‎2‎)⋃[π,‎3π‎2‎),‎‎-sinx,x∈(π‎2‎,π),‎ ‎∴函数y=|tanx|cosx0≤x<‎3π‎2‎,x‎≠‎π‎2‎的图象是C.故选C.‎ ‎5.BCD　由题图可知,A=2,T‎4‎‎=‎2π‎3‎-‎5π‎12‎=‎π‎4‎,∴T=‎2πω=π,则ω=2,‎ 又2‎×‎‎5π‎12‎+φ=π,∴φ=π‎6‎,满足0<|φ|<π,则f(x)=2sin2x+π‎6‎.‎ ‎∵fπ‎2‎=-1,∴f(x)的图象不关于直线x=π‎2‎对称;‎ ‎∵f-π‎12‎=0,∴f(x)的图象关于点-π‎12‎,0对称;‎ 由x∈-π‎3‎‎,‎π‎6‎,得2x+π‎6‎‎∈‎-π‎2‎‎,‎π‎2‎,则f(x)在区间-π‎3‎‎,‎π‎6‎上单调递增;由f(x)=2sin2x+π‎6‎=1,得sin2x+π‎6‎=‎1‎‎2‎,‎ 10‎ ‎∴2x+π‎6‎‎=‎π‎6‎+2kπ或2x+π‎6‎‎=‎‎5π‎6‎+2kπ,k∈Z.取k=0,得x=0或π‎3‎;取k=1,得x=π或‎4π‎3‎‎.∴‎函数y=1与y=f(x)-π‎12‎‎≤‎x‎≤‎‎23π‎12‎的图象的所有交点的横坐标之和为π‎3‎+π+‎‎4π‎3‎‎=‎8π‎3‎.‎ ‎6.BCD　a=6,4sinB=5sinC即4b=5c,设b=5t,c=4t,由36+16t2=25t2,可得t=‎4‎‎3‎,满足条件的△ABC可能是直角三角形,故A错误;‎ a=6,4sinB=5sinC,A=2C,可得B=π-3C,由正弦定理可得4b=5c,b=‎5c‎4‎,‎ 由bsinB‎=‎csinC,sinC≠0,‎ 可得4cos2C-1=‎5‎‎4‎,解得cosC=‎3‎‎4‎,sinC=‎7‎‎4‎,可得sinA=2sinCcosC=‎3‎‎7‎‎8‎,可得c=4,b=5,则a+b+c=15,故B正确;‎ S△ABC=‎1‎‎2‎bcsinA=‎‎15‎‎7‎‎4‎‎.‎ 设△ABC的内切圆半径为R,则R=‎2Sa+b+c‎=‎‎7‎‎2‎,‎ S△AOB=‎1‎‎2‎cR=‎7‎‎.‎故C正确.‎ 以BC的中点为坐标原点,BC所在直线为x轴,可得B(-3,0),C(3,0),‎ 又4sinB=5sinC,可得4b=5c,‎ 设A(m,n),‎ 可得4‎(m-3‎)‎‎2‎+‎n‎2‎=5‎(m+3‎)‎‎2‎+‎n‎2‎,平方可得16(m2+n2-6m+9)=25(m2+n2+6m+9),即有m2+n2+‎82‎‎3‎m+9=0,‎ 化为m+‎41‎‎3‎2+n2=‎40‎‎3‎2,‎ 10‎ 则A的轨迹为以-‎41‎‎3‎,0为圆心,半径为‎40‎‎3‎的圆,可得△ABC的面积的最大值为‎1‎‎2‎‎×‎6‎×‎‎40‎‎3‎=40,故D正确.‎ ‎7.π‎6‎‎,‎π‎4‎　‎3‎‎2‎‎2‎‎,‎‎4‎‎3‎‎3‎　(1)∵A=2B,A+B+C=π,∴C=π-3B,‎ ‎∵△ABC是锐角三角形,‎ ‎∴0<2B<π‎2‎且0<π-3B<π‎2‎,解得π‎6‎0,‎ 当0‎‎3‎‎2‎,且B为钝角,‎∴‎π‎2‎1时,当且仅当cosx‎2‎=1时,f(x)取得最小值,‎ 即f(x)min=2-4λ-1=-1,解得λ=‎1‎‎2‎,不满足λ>1,故舍去;‎ 当λ<‎1‎‎2‎时,当且仅当cosx‎2‎‎=‎‎1‎‎2‎时,f(x)取得最小值,‎ 即f(x)min=2‎×‎‎1‎‎4‎-4λ‎×‎‎1‎‎2‎-1=-1,解得λ=‎1‎‎4‎,满足λ<‎‎1‎‎2‎‎.‎ 综上所述,λ=‎‎1‎‎4‎‎.‎ 10‎