【数学】云南省玉溪市普通高中2021届高三上学期第一次教学质量检测（12月）试题（理） 16页

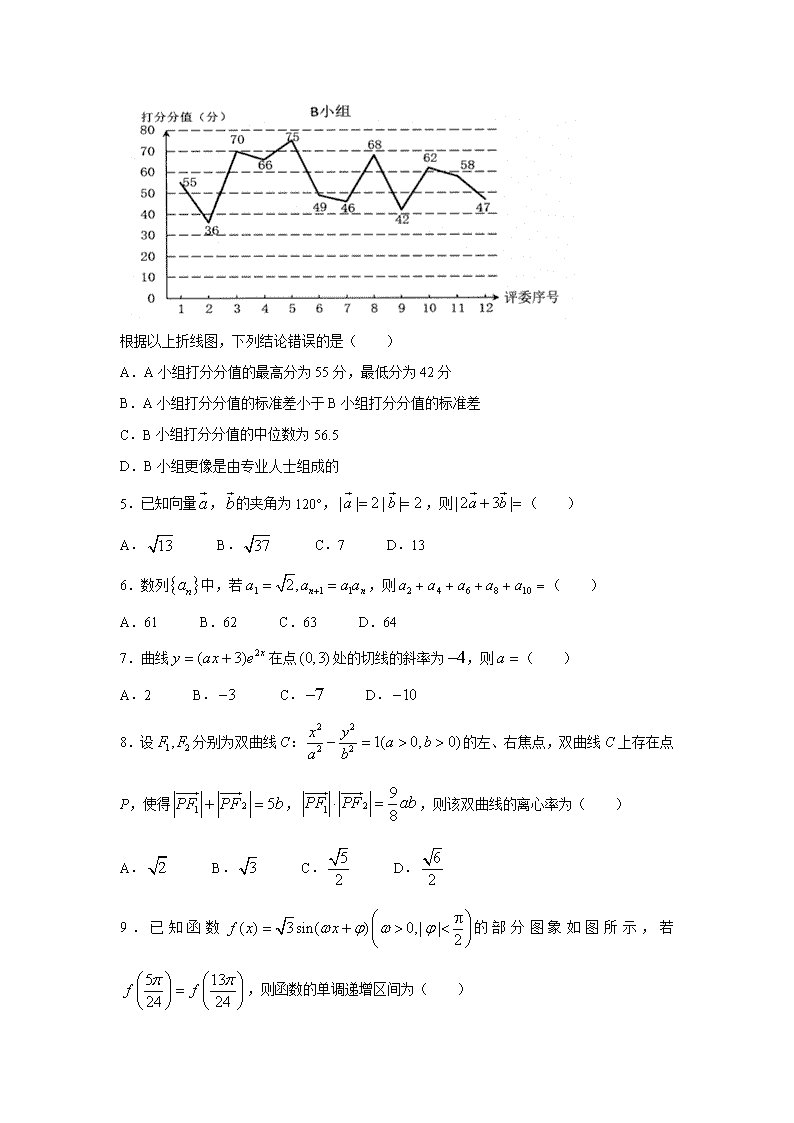
云南省玉溪市普通高中 2021 届高三上学期第一次教学质量 检测（12 月）数学试题（理） 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有 一项是符合题目要求的． 1．已知集合  2{ | 1}, | 0     A x x B x x x ，则  A B （ ） A． ( 1,1) B．[ 1,1) C． (0,1) D．[0,1) 2．设 2 i 1 iz   ，则在复平面内 z 对应的点位于（ ） A．第一象限 B．第二象限 C．第三象限 D．第四象限 3．已知 3 1cos 2 5        ，则 cos2  （ ） A． 23 25 B． 23 25  C． 24 25 D． 24 25  4．在一个文艺比赛中，12 名专业人士和 12 名观众代表各组成一个评判小组，给参赛选手 打分．根据两个评判小组对同一名选手的打分绘制了下面的折线图． 根据以上折线图，下列结论错误的是（ ） A．A 小组打分分值的最高分为 55 分，最低分为 42 分 B．A 小组打分分值的标准差小于 B 小组打分分值的标准差 C．B 小组打分分值的中位数为 56.5 D．B 小组更像是由专业人士组成的 5．已知向量  a，  b的夹角为 120°，| | 2 | | 2   a b ，则| 2 3 |   a b （ ） A． 13 B． 37 C．7 D．13 6．数列 na 中，若 1 1 12,  n na a a a ，则 2 4 6 8 10    a a a a a （ ） A．61 B．62 C．63 D．64 7．曲线 2( 3)  xy ax e 在点 (0,3) 处的切线的斜率为 4 ，则 a （ ） A．2 B． 3 C． 7 D． 10 8．设 1 2,F F 分别为双曲线 C： 2 2 2 2 1( 0, 0)   x y a ba b 的左、右焦点，双曲线 C 上存在点 P，使得 21 5   PF PF b， 21 9 8    PF PF ab ，则该双曲线的离心率为（ ） A． 2 B． 3 C． 5 2 D． 6 2 9 ． 已 知 函 数 ( ) 3sin( ) 0,| | 2f x x           的 部 分 图 象 如 图 所 示 ， 若 5 13 24 24           f f  ，则函数的单调递增区间为（ ） A． 3, ( )8 8k k k         Z B． 32 ,2 ( )8 8k k k         Z C． 3 7, ( )8 8k k k         Z D． 3 72 ,2 ( )8 8k k k         Z 10．已知直线 l： 1 y kx 与圆 O： 2 2 1 x y 相交于 M，N 两点，且MON 的面积 3 4 S ， 则 k （ ） A． 3 3  B． 3 C． 3 3 或 3 D． 3 3  或 3 11．已知正方体 1 1 1 1ABCD A B C D 的棱长为 3，E，F，G 分别为棱 1AA ， AB ， 1CC 上的 点，其中 1AE ， 2AF ， 3 2 CG ，平面 经过点 E，F，G，则 截此正方体所得的 截面为（ ） A．三角形 B．四边形 C．五边形 D．六边形 12．已知 99 1001 101, , ln101 100    a b e c ，则 a，b，c 的大小关系为（ ） A．  a b c B．  a c b C．  c a b D．  b a c 二、填空题：本题共 4 小题，每小題 5 分，共 20 分． 13．已知实数 x，y 满足 1 0 3 1 0 3          x y x y x ，则 2 z x y 的最小值是________． 14．公元前 6 世纪，古希腊毕达哥拉斯学派已经知道五种正多面体，即正四面体、正六面体、 正八面体、正十二面体、正二十面体．后来，柏拉图学派的泰阿泰德（Theaetetus）证明出 正多面体总共只有上述五种．如图就是五种正多面体的图形．现有 5 张分别画有上述五种多 面体的不同卡片（除画有的图形不同外没有差别），若从这 5 张不同的卡片中任取 2 张，则 没有取到画有“正四面体”卡片的概率为____________． 15．以下数表的构造思路源于我国南宋数学家杨辉所著的《详解九章算术》一书中的“杨辉 三角形”． 此表由若干个数字组成，从第二行起，每一行中的数字均等于其“肩上”两数之和．若每行的 第 一 个 数 构 成 有 穷 数 列  na ， 并 且 得 到 递 推 关 系 为 2 1 12 2 , 1   n n na a a ． 则 na _________． 16．在三棱锥 P ABC 中， 2  PA PB PC ，ABC 是正三角形，E 为 PC 中点，有 以下四个结论： ①若 PC BE ，则三棱锥 P ABC 的体积为 2 2 3 ； ②若 PC BE ，且三棱锥 P ABC 的四个顶点都在球 O 的球面上，则球 O 的体积为 6 ； ③若 PA BE ，则三棱锥 P ABC 的体积为 2 3 3 ； ④若 PA BE ，且三棱锥 P ABC 的四个顶点都在球 O 的球面上，则球 O 的表面积为12 ． 其中结论正确的序号为____________． 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17～21 题为必考 题，每个试题考生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（本小题满分 12 分） 如图，在ABC 中， 2AB AC ，BAC 的角平分线交 BC 于点 D． （1）求   ABD ADC S S 的值；（2）若 1, 2 AC BD ，求 AD的长． 18．（本小题满分 12 分） 物理学中常用“伏安法”测量电阻值（单位：欧姆），现用仪器测量某一定值电阻在不同电压 下的电流值测得一组数据  , ( 1,2, ,10) i ix y i ，其中， ix 和 iy 分别表示第 i 次测量数据 的电流（单位：安培）和电压（单位：伏特），计算得 10 1010 2 1 1 1 1 1 0 2.4, 12, 3.196, 0.6432           i i i i i i i i i x y x y x ． （1）用最小二乘法求出回归直线方程（ b 与 a 精确到 0.01）； （2）由“伏安法”可知，直线的斜率是电阻的估计值，请用计算得到的数据说明电阻的估计 值．附：回归直线的斜率和截距的最小二乘估计公式分别为： 1 22 1 ,          n n i i i i i x y nx y b a y bx x nx ． 19．（本小题满分 12 分） 如图所示，在正三棱柱 1 1 1ABC A B C 中， 1 2 AB AA ，E，F 分别是 AB ， AC 的中点． （1）求证： 1 1∥B C 平面 1A EF ； （2）若点 G 是线段 1 1B C 的中点，求二面角 1  A EF G 的正弦值． 20．（本小题满分 12 分） 已知椭圆 C： 2 2 2 2 1( 0)   x y a ba b 的离心率 1 2 e ，左、右焦点分别为 1F ， 2F ，抛物线 2 8y x 的焦点 F 恰好是该椭圆的一个顶点． （1）求椭圆 C 的方程； （2）记椭圆 C 与 x 轴交于 A，B 两点，M 是直线 1x 上任意一点，直线 MA，MB 与椭圆 C 的另一个交点分别为 D，E．求证：直线 DE 过定点 (4,0)H ． 21．（本小题满分 12 分） 已知函数 2( ) , ( )    xf x e mx g x x m （1）讨论 ( )f x 的单调性； （2）设函数 ( ) ( ) ( ) h x f x g x ，若 ( )h x 在[0, ) 上有且只有一个零点，求 m 的取值范 围． （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多做，则按所做的 第一题计分．作答时用 2B 铅笔在答题卡上把所选题目的题号涂黑． 22．[选修 4-4：坐标系与参数方程]（本小题满分 10 分） 在平面直角坐标系 xOy 中，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，直线 l 的极坐标方程为 3 cos sin 2 03       ，半圆 C 的极坐标方程为 1( [0, ])    ． （1）求直线 l 的直角坐标方程及 C 的参数方程； （2）若直线 l 平行于 l，且与 C 相切于点 D，求点 D 的直角坐标． 23．[选修 4-5：不等式选讲]（本小题满分 10 分） 已知函数 ( ) | | | | ( 0, 0)     f x x a x b a b ． （1）若 1 a b ，解不等式 ( ) 2f x ； （2）若 ( )f x 的值域是[2, ) ，且 1 1 2 1    ka b ，求 k 的最大值． 参考答案 一、选择题：本大题共 12 小题，每小题 5 分，共 60 分． 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C A A D A B D C A D C B 二、填空题：本大题共 4 小题，每小题 5 分，共 20 分． 题号 13 14 15 16 答案 2 3 5 2( 1) 2   nn ①②④ 三、解答题：本大题共 6 小题，共 70 分． 17．（本小题满分 12 分） 解：（1）∵ AD为BAC 的角平分线， ∴   BAD CAD ，即sin sin  BAD CAD ． 1 分 ∴ 1 sin2 1 sin2        ABD ADC AB AD BADS S AC AD CAD 2 分  AB AC ． 3 分 又∵ 2AB AC ， ∴ 2  ABD ADC S S ． 5 分 （2）由（1）知 2 AB BD AC CD 且 1, 2 AC BD ， ∴ 22, 2  AB CD ． 6 分 在ABD 中， 2 2 2 cos 2     AB AD BDBAD AB AD 2 24 2 2 2 2 4      AD AD AD AD ． 8 分 在ACD 中， 2 2 2 cos 2     AC AD CDCAD AC AD 2 21 11 2 2 2 1 2       AD AD AD AD ． 10 分 ∵   BAD CAD ， ∴ cos cos  BAD CAD ， ∴ 2 2 1 2 2 4 2   ADAD AD AD ， ∴ 1AD ． 12 分 18．（本小题满分 12 分） 解：（1） 10 1 0.2410    i i x x ， 1 分 10 1 1.210    i i y y ， 2 分 1 22 1 ˆ        n i i i n i i x y nx y b x nx 2 3.196 10 0.24 1.2 0.6432 10 0.24      4 分 0.316 0.0672  4.70 ， 6 分  1.2 4.70 0.24 0.072 0.07    a ． 8 分 所以，回归直线方程为  4.70 0.07 y x ． 10 分 （2）由“伏安法”可知，直线的斜率是电阻的估计值，所以电阻的估计值为 4.70 欧姆．12 分 19．（1）证明：在正三棱柱 1 1 1ABC A B C 中， 1 1//BC B C ． 1 分 ∵E，F 分别是 AB ， AC 的中点， ∴ EF 是ABC 的中位线，∴ //EF BC ． 2 分 又∵ 1 1//BC B C ，∴ 1 1//EF B C ． 3 分 又 1 1 B C 平面 1A EF ， EF 平面 1A EF ， ∴ 1 1 //B C 平面 1A EF ． 5 分 （2）解：向量法： 在正三棱柱 1 1 1ABC A B C 中， 取 1 1AC 的中点 H，连接 FH ，则 1//FH CC ． 在正ABC 中，连接 FB ，则 FB AC ． 又因为 1 2 AB AA ， 所以 3, 1 FB FC ． 如图，以 F 为原点建立空间直角坐标系 F xyz ． 7 分 1 3 1 3 1(0, 1,2), , ,0 , (0,0,0), , ,22 2 2 2             A E F G 1 1 3 1 3 1, , 2 , (0,1, 2), (0, 1, 2), , , 22 2 2 2                          A E A F GE GF ． 设 ( , , ) m x y z 为平面 1A EF 的一个法向量， 则 1 1 3 1 2 02 2 2 0                m A E x y z m A F y z ． ∴ 2 3 ,2,13        m ． （9 分） 同理可求，平面GEF 的一个法向量为∴ 2 3 ,2, 13        n ． 10 分 设二面角 1  A EF G 的平面角为 ， ∴ 4 4 1 133cos 1919 19 3 3       ， 11 分 所以二面角 1  A EF G 的正弦值为 8 3 19 ． 12 分 几何法： 在正三棱柱 1 1 1ABC A B C 中， 取 BC 中点 D，连接 AD，且  AD EF O ， 连接 1AO ，GO 6 分 则 AD BC ，又 1 AA BC ， 1  AA AD A ， ∴ BC 平面 1AOG ． 7 分 由（1）知： //EF BC ， ∴ EF 平面 1AOG ． 8 分 ∴ 1AOG 即为二面角 1  A EF G 的平面角，记为 ． 9 分 连接 1AG ， 1AOG 中， 1 3 194 4 2   AO ， 3 194 4 2   GO ， 1 3AG ， 由余弦定理得： 19 19 3 134 4cos 1919 192 2 2        ． 11 分 所以二面角 1  A EF G 的正弦值为 8 3 19 ． 12 分 20．解：（本小题满分 12 分） （1）因为椭圆 C 的离心率 1 2 e ，所以 1 2 c a ，即 2a c ． 1 分 因为抛物线 2 8y x 的焦点 (2,0)F 恰好是该椭圆的一个顶点， 2 分 所以 2a ，所以 1, 3 c b ． 3 分 所以椭圆 C 的方程为 2 2 14 3  x y ． 4 分 （2）由（1）可得 ( 2,0)A ， (2,0)B ，设点 M 的坐标为 (1, )m ， 直线 MA的方程为： ( 2)3  my x ． 将 ( 2)3  my x 与 2 2 14 3  x y 联立消去 y 整理 得：  2 2 2 24 27 16 16 108 0    m x m x m ． 5 分 设点 D 的坐标为  ,D Dx y ，则 2 2 16 1082 4 27   D mx m ， 6 分 故 2 2 54 8 4 27  D mx m ，则   2 3623 4 27    D D m my x m ． 7 分 直线 MB 的方程为： ( 2)  y m x ， 将 ( 2)  y m x 与 2 2 14 3  x y 联立消去 y 整理得：  2 2 2 24 3 16 16 12 0    m x m x m ． 8 分 设点 E 的坐标为  ,E Ex y ，则 2 2 16 122 4 3  E mx m ， 9 分 故 2 2 8 6 4 3  E mx m ，则   2 122 4 3     E E my m x m ． 10wv 直线 HD 的斜率为  1 22 2 36 6 4 4 954 8 4 4 27        D D y m mk x mm m ， 直线 HE 的斜率为  2 22 2 12 6 4 4 98 6 4 4 3        E E y m mk x mm m ． 11 分 因为 1 2k k ，所以直线 DE 经过定点 H． 12 分 21．（本小题满分 12 分） 解：（1） ( )  xf x e m 1 分 ①若 0m ，则 ( ) 0 f x ，∴ ( )f x 在 R 上单调递增． 2 分 ②若 0m ，令 ( ) 0 f x ，则 lnx m ， 3 分 当 ( ,ln ) x m 时， ( ) 0 f x ；当 (ln , ) x m 时， ( ) 0 f x ， ∴ ( )f x 在 ( ,ln ) m 上单调递减，在 (ln , )m 上单调递增． 综上，当 0m 时， ( )f x 在 R 上单调递增；当 0m 时， ( )f x 在 ( ,ln ) m 上单调递减， 在 (ln , )m 上单调递增． 4 分 （2）由题意知： 2( )    xh x e mx x m ，则 ( ) 2   xh x e x m ， 5 分 易知 ( )h x 在(0, ) 上单调递增，且 (0) 1 h m ． ①若 1m ，则 ( ) 0 h x ，∴ ( )h x 在 (0, ) 上单调递增， ∵ ( )h x 在[0, ) 上有且只有一个零点， (0) 1 , (1) 1 0    h m h e ， ∴ (0) 1 0  h m ，即 1 m ． ∴当 1 m 时， ( )h x 在[0, ) 上有且只有一个零点． 7 分 ②若 1m ，则 (0) 1 0, (ln ) 2ln 0     h m h m m ， ∴存在 0 (0,ln )x m ，使  0 0 h x ，即 0 02 xe x m ， 8 分 ∴当  00,x x 时， ( ) 0 h x ；当  0, x x 时， ( ) 0 h x ． ∴ ( )h x 在  00, x 上单调递减，在  0,x 上单调递增， 又 (0) 1 0  h m ， ( ) 0  mh m e m ， ( )h x 在[0, ) 上有且只有一个零点， ∴  0 0h x ，即 0 2 0 0 0   xe mx x m ． 把 0 02 xm e x 代入上式可知：  0 0 02 0  xx e x ，∴ 0 2x ， 10 分 从而 2 4 m e ． 11 分 综上，当 1 m 或 2 4 m e 时， ( )h x 在[0, ) 上有且只有一个零点． 12 分 22．（本小题满分 10 分） 解：（1）直线 l 的普通方程为 3 2 03   x y ； 2 分 C 的普通方程为 2 2 1(0 1)   x y y ． 可得 C 的参数方程为 cos sin    x t y t （t 为参数， 0  t  ）． 5 分 （2）由点 D 在曲线 C 上可设 (cos ,sin )D t t ， 6 分 由题意可知曲线 C 在点 D 处的切线斜率为 3 3  ， 7 分 tan 3, 3  t t  ． 8 分 故 D 的直角坐标为 cos ,sin3 3       ，即 1 3,2 2       ． 10 分 23．（本小题满分 10 分） 解：（1）∵ 1a ， 1b ， ∴ 2 , 1 ( ) | 1| | 1| 2, 1 1 2 , 1             x x f x x x x x x 2 分 当 1x 时， ( ) 2f x 化为 1x ，不等式的解为 1x ； 当 1 1  x 时， ( ) 2f x ，不等式的解为  ； 当 1 x 时， ( ) 2f x 化为 2 2 1    x x ，所以不等式的解为 1 x ． 4 分 综上所述，不等式的解集为{ | 1 1}  或x x x ． 5 分 （2）∵ ( ) | | | | |( ) ( ) | | |         f x x a x b x a x b a b ， 6 分 当且仅当 ( )( ) 0  x a x b 时取“=”号． 又 ( )f x 的值域是[2, ) ， 所以| | 2 a b ，∵ 0, 0 a b ． ∴ 2 2 1 5      a b a b ． 7 分 ∵ 1 1 2 1 2 1( 2 1) 2 2 2 42 1 1 2 1 2                              a b a ba b a b b a b a （当且仅当 1 2 2 1    b a a b ，即 0.5, 1.5 a b 时取“=”号）， ∴ 1 1 4 2 1 5   a b ，当且仅当 0.5, 1.5 a b 时取“=”号． 9 分 又∵ 1 1 2 1    ka b 恒成立，∴ 4 5 k ， 故 k 的最大值是 4 5 ． 10 分