2018届二轮复习（文）专题七解析几何3 26页

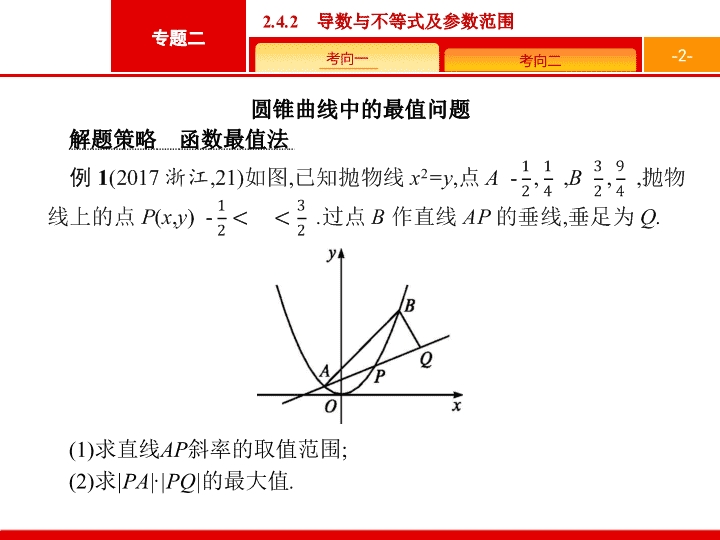
7 . 3 . 2 　 圆锥曲线中的最值 、 范围 、证明问题 - 2 - 圆锥曲线中的最值问题 解题策略 　 函数最值法   (1) 求直线 AP 斜率的取值范围 ; (2) 求 |PA| · |PQ| 的最大值 . - 3 - (2) 以 AP 斜率 k 为自变量 , 表示出 |PA| , 联立直线 AP 与 BQ 的方程用 k 表示出点 Q 的横坐标 , 从而用 k 表示出 |PQ| , 得到 |PA| · |PQ| 是关于 k 的函数 , 用函数求最值的方法求出最大值 . - 4 - 所以 |PA|·|PQ|=- ( k- 1)( k+ 1) 3 . 令 f ( k ) =- ( k- 1)( k+ 1) 3 , 因为 f' ( k ) =- (4 k- 2)( k+ 1) 2 , 解题心得 圆锥曲线中的有关平面几何图形面积的最值问题 , 通过某一变量表示出图形的面积的函数表达式 , 转化为函数的最值问题 , 然后求导确定函数单调性求最值 , 或利用基本不等式 , 或利用式子的几何意义求最值 . - 5 - 对点训练 1 (2017 山西临汾三模 , 文 20) 已知抛物线 y 2 = 8 x 与垂直于 x 轴的直线 l 相交于 A , B 两点 , 圆 C : x 2 +y 2 = 1 分别与 x 轴正、负半轴相交于点 P , N , 且直线 AP 与 BN 交于点 M. (1) 求证 : 点 M 恒在抛物线上 ; (2) 求 △ AMN 面积的最小值 . (1) 证明 设 A ( x 1 , y 1 ), B ( x 1 , -y 1 )( x 1 > 0), 由题意 , P (1,0), N ( - 1,0), 直线 AP 的方程为 ( x 1 - 1) y=y 1 ( x- 1), 直线 BN 的方程为 ( x 1 + 1) y=-y 1 ( x+ 1), 即点 M 恒在抛物线上 . - 6 - (2) 由 (1) 可得 △ AMN 面积 - 7 - 圆锥曲线中的范围问题 ( 多维探究 ) 解题策略一 　 条件转化法   (1) 求椭圆 E 的方程 ; (2) 设过点 P 的动直线 l 与 E 相交于 M , N 两点 , 当坐标原点 O 位于以 MN 为直径的圆外时 , 求直线 l 斜率的取值范围 . - 8 - 难点突破 (1) △ ABP 是等腰直角三角形 ⇒ a= 2; 由 , 得 Q 点坐标 , 代入椭圆方程求得 b ; (2) 设直线 y=kx- 2, 代入椭圆方程 , 由根与系数的关系及 Δ> 0 得 k 的一个范围 , 由原点 O 在以 MN 为直径的圆外 ⇒ > 0 ⇒ x 1 x 2 +y 1 y 2 > 0 ⇒ 关于 k 的不等式 ⇒ k 的另一范围 , 取两个 k 的范围的交集得结论 . 由向量数量积的坐标公式 , 即可求得直线 l 斜率的取值范围 . 解 (1) 由题意知 △ ABP 是等腰直角三角形 , a= 2, B (2,0 ), - 9 - (2) 由题意可知 , 直线 l 的斜率存在 , 设方程为 y=kx- 2, 设 M ( x 1 , y 1 ), N ( x 2 , y 2 ), 即 x 1 x 2 +y 1 y 2 > 0, 则 x 1 x 2 +y 1 y 2 =x 1 x 2 + ( kx 1 - 2)( kx 2 - 2) - 10 - 解得 k 2 < 4, ② 解题心得 求某一量的取值范围 , 要看清与这个量有关的条件有几个 , 有几个条件就可转化为几个关于这个量的不等式 , 解不等式取交集得结论 . - 11 - 对点训练 2 经过 原点的直线与 椭圆 C : ( a>b> 0 ) 交于 A , B 两点 , 点 P 为椭圆上不同于 A , B 的一点 , 直线 PA , PB 的斜率均存在 , 且直线 PA , PB 的斜率之积为 - . (1) 求椭圆 C 的离心率 ; (2) 设 F 1 , F 2 分别为椭圆的左、右焦点 , 斜率为 k 的直线 l 经过椭圆的右焦点 , 且与椭圆交于 M , N 两点 . 若点 F 1 在以 |MN| 为直径的圆内部 , 求 k 的取值范围 . - 12 - 解 (1) 设 A ( x 1 , y 1 ), 则 B ( -x 1 , -y 1 ), P ( x 0 , y 0 ), ∵ 点 A , B , P 三点均在椭圆上 , - 13 - (2) 设 F 1 ( -c ,0), F 2 ( c ,0), 直线 l 的方程为 y=k ( x-c ), 记 M ( x 3 , y 3 ), N ( x 4 , y 4 ), - 14 - 解题策略二 　 构造函数法   (1) 求椭圆 C 的方程 ; (2) 设直线 PQ 方程 , 代入椭圆方程 , 利用根与系数的关系及向量数量积的坐标 , 将 表示 为直线斜率 k 的函数 , 由函数的单调性求得函数的值域 , 即所求量的取值范围 . - 15 - (2) 当 PQ 的斜率存在时 , 设直线 PQ 的方程为 y=kx+ 2, 点 P , Q 的坐标分别为 ( x 1 , y 1 ),( x 2 , y 2 ), - 16 - 解题心得 求直线与圆锥曲线的综合问题中 , 求与直线或与圆锥曲线有关的某个量 d 的范围问题 , 依据已知条件建立关于 d 的函数表达式 , 转化为求函数值的范围问题 , 然后用函数的方法或解不等式的方法求出 d 的范围 . - 17 - 对点训练 3 如 图 , 设抛物线 y 2 = 2 px ( p> 0) 的焦点为 F , 抛物线上的点 A 到 y 轴的距离等于 |AF|- 1 . (1) 求 p 的值 ; (2) 若直线 AF 交抛物线于另一点 B , 过 B 与 x 轴平行的直线和过 F 与 AB 垂直的直线交于点 N , AN 与 x 轴交于点 M. 求 M 的横坐标的取值范围 . - 18 - 解 (1) 由题意可得 , 抛物线上点 A 到焦点 F 的距离等于点 A 到直线 x=- 1 的距离 , (2) 由 (1) 得 , 抛物线方程为 y 2 = 4 x , F (1,0), 可设 A ( t 2 ,2 t ), t ≠0, t ≠ ± 1 . 因为 AF 不垂直于 y 轴 , 可设直线 AF : x=sy+ 1( s ≠0), - 19 - 所以 m< 0 或 m> 2 . 经检验 , m< 0 或 m> 2 满足题意 . 综上 , 点 M 的横坐标的取值范围是 ( -∞ ,0) ∪ (2, +∞ ) . - 20 - 圆锥曲线中的证明问题 解题策略 　 转化法   例 4 已知 A 是椭圆 E : = 1 的左顶点 , 斜率为 k ( k> 0) 的直线交 E 于 A , M 两点 , 点 N 在 E 上 , MA ⊥ NA. (1) 当 |AM|=|AN| 时 , 求 △ AMN 的面积 ; (2) 当 2 |AM|=|AN| 时 , 证明 : < k< 2 . 难点突破 (1) A 是椭圆的左顶点及 MA ⊥ NA ⇒ AM 的倾斜角 为 ⇒ AM 的方程再代入椭圆方程 ⇒ y M ⇒ △ AMN 的面积 . (2) MA ⊥ NA ⇒ k MA · k NA =- 1 ⇒ 用 k 表示出两条直线方程 , 分别与椭圆联立 , 用 k 表示出 |AM| 与 |AN| ,2 |AM|=|AN| ⇒ f ( k ) = 0 ⇒ k 是函数 f ( t ) 的零点 , 对 f ( t ) 求导确定 f ( t ) 在 (0, +∞ ) 单调递增 , 再由零点存在性定理求出 k 的范围 . - 21 - (1) 解 设 M ( x 1 , y 1 ), 则由题意知 y 1 > 0 . 由已知及椭圆的对称性知 , 直线 AM 的倾斜角 为 . 又 A ( - 2,0), 因此直线 AM 的方程为 y=x+ 2 . - 22 - 即 4 k 3 - 6 k 2 + 3 k- 8 = 0 . 设 f ( t ) = 4 t 3 - 6 t 2 + 3 t- 8, 则 k 是 f ( t ) 的零点 . f' ( t ) = 12 t 2 - 12 t+ 3 = 3(2 t- 1) 2 ≥ 0, 所以 f ( t ) 在 (0, +∞ ) 单调递增 . - 23 - 解题心得 圆锥曲线中的证明问题涉及证明的范围比较广 , 但无论证明什么 , 其常用方法有直接法和转化法 , 对于转化法 , 先是对已知条件进行化简 , 根据化简后的情况 , 将证明的问题转化为另一问题 , 如本例中把证明 k 的范围问题转化为方程的零点 k 所在的范围问题 . - 24 - 对点训练 4 (2017 贵州贵阳二模 , 文 20 ) 已知椭圆 C : = 1( a> 0) 的焦点在 x 轴上 , 且椭圆 C 的焦距为 2 . (1) 求椭圆 C 的标准方程 ; (2) 过点 R (4,0) 的直线 l 与椭圆 C 交于 P , Q 两点 , 过 P 作 PN ⊥ x 轴且与椭圆 C 交于另一点 N , F 为椭圆 C 的右焦点 , 求证 : N , F , Q 三点在同一条直线上 . ∵ 椭圆 C 的焦距为 2, 且 a 2 -b 2 =c 2 , ∴ a 2 - (7 -a 2 ) = 1, 解得 a 2 = 4, - 25 - (2) 证明 由题知直线 l 的斜率存在 , 设 l 的方程为 y=k ( x- 4), 点 P ( x 1 , y 1 ), Q ( x 2 , y 2 ), N ( x 1 , -y 1 ), - 26 - 即直线 QN 过点 (1,0), 又椭圆 C 的右焦点坐标为 F (1,0), ∴ N , F , Q 三点在同一条直线上 .