2019届二轮复习第十章算法初步、统计与统计案例10 40页

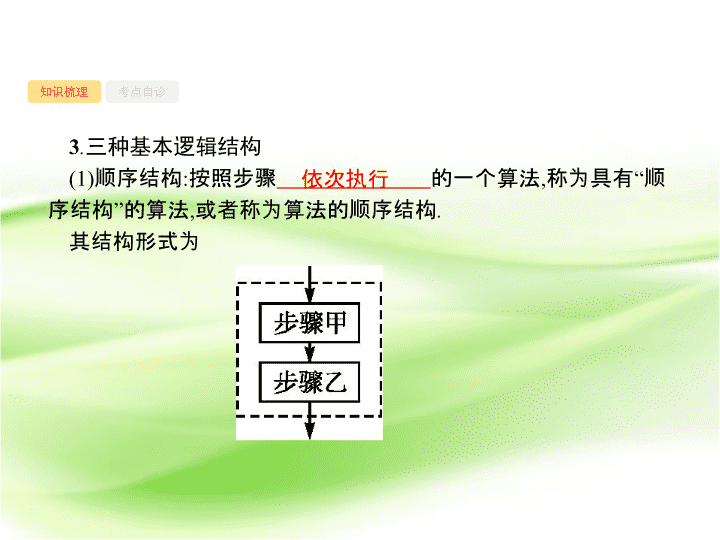
10 . 1 　 算法初步 - 2 - 知识梳理 考点自诊 1 . 算法的含义 在解决某些问题时 , 需要设计出一系列可操作或可计算的 　　　 , 通过实施这些 　　　　　 来解决问题 , 通常把这些 　　　　　 称为解决这些问题的算法 .   2 . 算法框图 在算法设计中 , 算法框图可以准确、清晰、直观地表达解决问题的思想和步骤 , 算法框图的三种基本结构 : 　　　　　　　 、 　　　　　　　 、 　　　　　　　 .   步骤 步骤 步骤 顺序结构 　 选择结构 　 循环结构 - 3 - 知识梳理 考点自诊 3 . 三种基本逻辑结构 (1) 顺序结构 : 按照步骤 　　　　　　　 的一个算法 , 称为具有 “ 顺序结构 ” 的算法 , 或者称为算法的顺序结构 .   其结构形式为 依次执行 - 4 - 知识梳理 考点自诊 (2) 选择结构 : 需要 　　　　　　　　 , 判断的结果决定后面的步骤 , 像这样的结构通常称作选择结构 .   其结构形式为 进行判断 - 5 - 知识梳理 考点自诊 (3) 循环结构 : 指从某处开始 , 按照一定条件反复执行某些步骤的情况 . 反复执行的处理步骤称为 　　　　　　 .   其基本模式为 循环体 - 6 - 知识梳理 考点自诊 4 . 基本算法语句 任何一种程序设计语言中都包含五种基本的算法语句 , 它们分别是 : 　　　　　　　 、输出语句、 　　　　　　　 、条件语句和 　　　　　　　 .   5 . 赋值语句 (1) 一般形式 : 变量 = 表达式 . (2) 作用 : 将表达式所代表的值赋给变量 . 输入语句 赋值语句 循环语句 - 7 - 知识梳理 考点自诊 6 . 条件语句 (1)If—Then—Else 语句的一般格式为 : If 　条件　　 Then 语句 1 Else 语句 2 End 　 If (2)If—Then 语句的一般格式是 : If 　条件　　 Then 语句 End 　 If - 8 - 知识梳理 考点自诊 7 . 循环语句 (1)For 语句的一般格式 : For 循环变量 = 初始值 To 终值 循环体 Next (2)Do Loop 语句的一般格式 : Do 　 循环体 Loop While 条件为真 - 9 - 知识梳理 考点自诊 1 . 判断下列结论是否正确 , 正确的画 “ √ ”, 错误的画 “ × ” . (1) 一个 算法框图 一定包含顺序结构 , 但不一定包含 选择 结构和循环结构 . ( 　　 ) (2) 选择 结构的出口有两个 , 但在执行时 , 只有一个出口是有效的 . ( 　　 ) (3) 输入框只能紧接开始框 , 输出框只能紧接结束框 . ( 　　 ) (4) 输入语句可以同时给多个变量赋值 . ( 　　 ) (5) 在算法语句中 , x=x+ 1 是错误的 . ( 　　 ) × √ √ √ × - 10 - 知识梳理 考点自诊 2 . (2018 全国 2, 文 8) 为计算 , 设计了下面的程序框图 , 则在空白框中应填入 ( 　　 ) A. i=i+ 1 B. i=i+ 2 C. i=i+ 3 D. i=i+ 4 B - 11 - 知识梳理 考点自诊 3 . (2018 四川成都考前模拟 ,7) 我国古代数学著作《孙子算经》中有这样一道算术题 :“ 今有物不知其数 , 三三数之剩一 , 五五数之剩三 , 七七数之剩六 , 问物几何 ?” 人们把此类题目称为 “ 中国剩余定理 ” . 若正整数 N 除以正整数 m 后的余数为 n , 则记为 N ≡ n (mod m ), 例如 10 ≡ 2(mod4) . 现将该问题以程序框图给出 , 执行该程序框图 , 则输出的 n 等于 ( 　　 ) A.13 B.11 C.15 D.8 A 解析 : 该程序框图的作用是求被 3 除后余数是 1, 被 5 除后余数是 3, 所有选项中只有 13 满足 . - 12 - 知识梳理 考点自诊 4 . (2017 全国 3, 文 8) 执行下面的程序框图 , 为使输出 S 的值小于 91, 则输入的正整数 N 的最小值为 ( 　　 ) A.5 B.4 C.3 D.2 D - 13 - 知识梳理 考点自诊 解析 : 程序运行过程如下表所示 : 此时 S= 90 < 91 首次满足条件 , 程序需在 t= 3 时跳出循环 , 即 N= 2 为满足条件的最小值 , 故选 D . - 14 - 知识梳理 考点自诊 5 . 运行如图所示的框图对应的程序 , 输出的结果为 　　　　　 .  1 - 15 - 考点 1 考点 2 考点 3 算法的基本结构 ( 多考向 ) 考向 1 　 顺序结构与 选择 结构 例 1 (1)(2018 山西大同二测 ,6) 对任意非零实数 a , b , 若 a*b 的运算原理如图所示 , 则 = ( 　　 ) A.1 B.2 C.3 D.4 A - 16 - 考点 1 考点 2 考点 3 (2)(2018 福建泉州 5 月质检 ,9) 执行如图所示的程序框图 , 若输入 x= 1, 则输出 a , b 的值分别为 ( 　　 ) A.sin 1,cos 1 B.sin 1,sin 1 C.cos 1,cos 1 D.cos 1,sin 1 D - 17 - 考点 1 考点 2 考点 3 - 18 - 考点 1 考点 2 考点 3 思考 应用顺序结构与 选择结构 时应注意什么 ? 解题心得 应用顺序结构 与 选择结构 的注意点 : (1) 顺序结构 : 顺序结构是最简单的算法结构 , 语句与语句之间、框与框之间是按从上到下的顺序进行的 . (2) 选择结构 : 利用 选择结构 解决算法问题时 , 重点是判断框 , 是否满足判断框内的条件 , 对应的下一图框中的内容是不一样的 , 故要重点分析判断框内的条件是否满足 . - 19 - 考点 1 考点 2 考点 3 对点训练 1 (1)(2018 福建漳州 5 月质检 , 文 8) 执行如图所示的程序框图 , 若输入 x= 64, 则输出的结果为 ( 　　 ) A.2 B.3 C.4 D.5 C - 20 - 考点 1 考点 2 考点 3 (2) 运行如图所示的程序框图 , 如果输出的 t ∈ ( - 2,2], 那么输入 x 的范围是 ( 　　 ) D - 21 - 考点 1 考点 2 考点 3 - 22 - 考点 1 考点 2 考点 3 考向 2 　 循环结构 A .A> 1 000 和 n=n+ 1 B .A> 1 000 和 n=n+ 2 C .A ≤ 1 000 和 n=n+ 1 D .A ≤ 1 000 和 n=n+ 2 D - 23 - 考点 1 考点 2 考点 3 (2)(2017 全国 2, 文 10) 执行下面的程序框图 , 如果输入的 a=- 1, 则输出的 S= ( 　　 ) A . 2 B . 3 C . 4 D . 5 B - 24 - 考点 1 考点 2 考点 3 (2) 程序框图运行如下 : a=- 1, S= 0, K= 1, 进入循环 , S= 0 + ( - 1) × 1 =- 1, a= 1, K= 2; S=- 1 + 1 × 2 = 1, a=- 1, K= 3; S= 1 + ( - 1) × 3 =- 2, a= 1, K= 4; S=- 2 + 1 × 4 = 2, a=- 1, K= 5; S= 2 + ( - 1) × 5 =- 3, a= 1, K= 6; S=- 3 + 1 × 6 = 3, a=- 1, K= 7, 此时退出循环 , 输出 S= 3 . 故选 B . - 25 - 考点 1 考点 2 考点 3 思考 循环结构的思维分析过程是怎样的 ? 解题心得 循环结构的一般思维分析过程是 : (1) 分析进入或退出循环体的条件 , 确定循环次数 . (2) 结合初始条件和输出结果 , 分析控制循环的变量应满足的条件或累加、累乘的变量的表达式 . (3) 辨析循环结构的功能 . - 26 - 考点 1 考点 2 考点 3 对点训练 2 (1)(2018 广东湛江二模 ,8) 执行如图的程序框图 , 输入 N= 2 018, 则输出的 S= ( 　　 ) B - 27 - 考点 1 考点 2 考点 3 (2)(2018 重庆三模 ,9) 《九章算术》里有一段叙述 : 今有良马与驽马发长安至齐 , 齐去长安一千一百二十五里 , 良马初日行一百零三里 , 日增十三里 ; 驽马初日行九十七里 , 日减半里 ; 良马先至齐 , 复还迎驽马 , 二马相逢 . 根据该问题设计程序框图如下 , 若输入 a= 103, b= 97, 则输出 n 的值是 ( 　　 ) A.8 B.9 C.12 D.16 B - 28 - 考点 1 考点 2 考点 3 - 29 - 考点 1 考点 2 考点 3 算法框图 的应用 ( 多考向 ) 考向 1 　 程序框图在函数中的应用 例 3 (2017 山东 , 文 6) 执行右面的程序框图 , 当输入的 x 的值为 4 时 , 输出的 y 的值为 2, 则空白判断框中的条件可能为 ( 　　 ) A. x> 3 　　　 B. x> 4 C. x ≤ 4 D. x ≤ 5 B 解析 : 因为输入的 x 的值为 4, 输出的 y 的值为 2, 所以程序运行 y= log 2 4 = 2 . 故 x= 4 不满足判断框中的条件 , 所以空白判断框中应填 x> 4 . - 30 - 考点 1 考点 2 考点 3 思考 求解本例题的关键是什么 ? 解题心得 与函数有关的程序框图问题大多是选择结构的程序框图 , 实质是与分段函数有关的问题 . 处理办法是仔细阅读框图 , 把选择结构所实现的程序功能弄清楚 , 可能是分段函数求函数值、分段函数求值域 , 也可能是解决一个多分支问题 . 总而言之 , 把选择结构所要表达的各分支的功能及条件弄清楚 , 然后根据条件选择某一分支 , 是解决这类问题的关键 . 求解中可能需要利用分类讨论思想 . - 31 - 考点 1 考点 2 考点 3 对点训练 3 一程序框图如图所示 , 如果输出的函数值在区间 [1,2] 上 , 那么输入实数 x 的取值范围是 ( 　　 )   A.( -∞ ,0) B.[ - 1,0] C.[1, +∞ ) D.[0,1] D 解析 : 根据题意 , 得当 x ∈ [ - 2,2] 时 , f ( x ) = 2 x , ∴ 1 ≤ 2 x ≤ 2, ∴ 0 ≤ x ≤ 1; 当 x ∉ [ - 2,2] 时 , f ( x ) = 3, 不符合题意 , ∴ x 的取值范围是 [0,1] . - 32 - 考点 1 考点 2 考点 3 考向 2 　 程序框图在数列中的应用 例 4 执行如图所示的程序框图 , 则输出的结果是 　　　　　 .  - 33 - 考点 1 考点 2 考点 3 思考 本例中的程序框图的作用是什么 ? 解题心得 与数列有关的程序框图多是循环结构的程序框图 , 解决此类问题 , 在清楚循环体、变量的初始值和循环的终止条件分别是什么的基础上 , 模拟电脑的运行步骤 . 当循环次数较少时 , 列出每一步的运行结果 , 直至程序结束 , 自然就得出答案 ; 当循环次数较多时 , 逐一列出前面的若干步骤 , 观察、归纳规律 , 从而得出答案 . 这是最常用、最有效、最适合学生认知水平的方法 . - 34 - 考点 1 考点 2 考点 3 对点训练 4 (2018 陕西榆林四模 ,8) 右图的程序框图的算法思路源于我国古代数学名著《数书九章》中的 “ 中国剩余定理 ” . 已知正整数 n 被 3 除余 2, 被 7 除余 4, 被 8 除余 5, 求 n 的最小值 . 执行该程序框图 , 则输出的 n= ( 　　 ) A.50 　 B.53 C.59 D.62 B 解析 : 模拟程序运行 , 变量 n 值依次为 1 229,1 061,893,725,557,389,221,53, 此时不符合循环条件 , 输出 n= 53, 故选 B . - 35 - 考点 1 考点 2 考点 3 基本算法语句 例 5 如果下面的程序执行后输出的结果是 11 880, 那么 While 后面的条件应为 ( 　　 ) i=12 s=1 Do s=s i i=i-1 Loop 　 While 　条件 Next 输出　 s A.i < 10 B.i <= 10 C.i <= 9 D.i < 9 D - 36 - 考点 1 考点 2 考点 3 解析 : 因为输出的结果是 11 880, 即 s= 1 × 12 × 11 × 10 × 9, 所以程序循环了 4 次 , 所以 While 后面的 “ 条件 ” 应为 i < 9 . 故选 D . 思考 解决算法语句问题的一般思路是什么 ? 解题心得 解决算法语句问题的一般思路是 : 首先通读全部语句 , 把它翻译成数学问题 ; 然后领悟该语句的功能 ; 最后根据语句的功能运行程序 , 解决问题 . - 37 - 考点 1 考点 2 考点 3 对点训练 5 按照如图程序运行 , 则输出 K 的值是 　　　　　 .  3 X=3 K=0 Do 　 X=2 X+1 　 K=K+1 Loop 　 While 　 X>16 Next 输出　 K 解析 : 第一次循环 , X= 7, K= 1; 第二次循环 , X= 15, K= 2; 第三次循环 , X= 31, K= 3; 终止循环 , 输出 K 的值是 3 . - 38 - 考点 1 考点 2 考点 3 1 . 在设计一个算法的过程中要牢记它的五个特征 : 概括性、逻辑性、有穷性、不唯一性、普遍性 . 2 . 在画程序框图时要进行结构的选择 . 若所要解决的问题不需要分情况讨论 , 则只用顺序结构就能解决 ; 若所要解决的问题需要分若干种情况讨论 , 则必须引入选择结构 ; 若所要解决的问题要进行多次重复的步骤 , 且这些步骤之间又有相同的规律 , 则必须引入变量 , 应用循环结构 . 3 . 利用循环结构表示算法的特点是先执行循环体再判断 . 当判断框内的条件不满足时继续执行循环体 , 当条件满足时输出结果 , 结束算法 . - 39 - 考点 1 考点 2 考点 3 4 . 需要输入信息时用输入语句 , 需要输出信息时用输出语句 , 当变量需要的数据较少或给变量赋予算式时 , 用赋值语句 , 当变量需要输入多组数据且程序重复使用时 , 使用循环语句较好 . 5 . 完善程序框图中的条件是程序框图问题中难度较大的一类问题 , 解决此类问题 , 应结合初始条件和输出的结果 , 分析控制循环的变量应满足的条件或累加、累乘的变量的表达式 , 明确进入循环体时变量的情况、累加或累乘变量的变化 . 具体解题方法有以下两种 : 一是先假定空白处填写的条件 , 再正面执行程序 , 来检验填写的条件是否正确 ; 二是根据结果进行回溯 , 直至确定填写的条件 . - 40 - 考点 1 考点 2 考点 3 1 . 注意起止框与处理框、判断框与输入、输出框的不同 . 2 . 赋值语句不能与等号相混淆 , 赋值号左边只能是变量名字 , 而不是表达式 , 赋值号左右不能对换 , 在一个赋值语句中只能给一个变量赋值 , 不能出现多个 “ = ” .