人教版高中数学选修1-1课件：5_导数在研究函数中的应用 24页

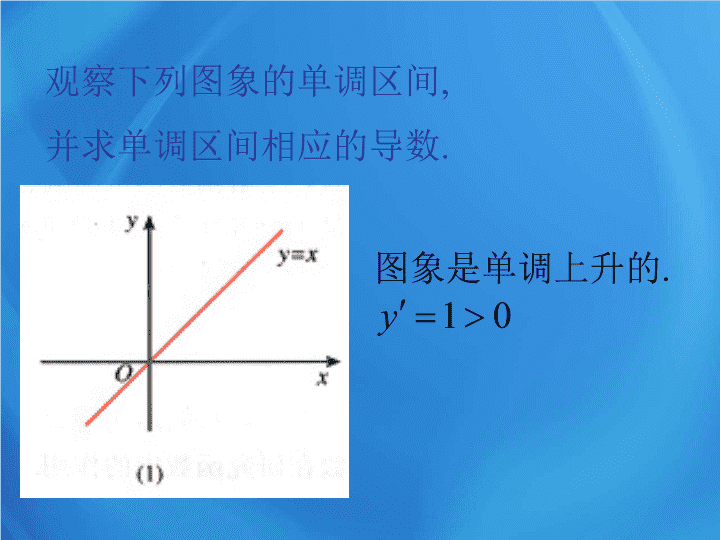
函数的单调性与导数 知识回顾 判断函数单调性有哪些方法？ 比如：判断函数 的单调性。 x y o 函数在 上为 ____ 函数， 在 上为 ____ 函数。 图象法 定义法 减 增 如图： 图象是单调上升的 . 观察下列图象的单调区间 , 并求单调区间相应的导数 . 图象是单调下降的 . 在 x ∈( - ∞,0) 内 图象是单调上升的 . 在 x ∈( 0,+∞) 内 图象是单调上升的 . 图象是单调下降的 . 在 x ∈( - ∞,0) 内 图象是单调下降的 . 在 x ∈( 0,+∞) 内 函数的单调性与其导函数正负的关系 : 当函数 y = f ( x ) 在某个区间内可导时， 如果 , 则 f ( x ) 为增函数； 如果 , 则 f ( x ) 为减函数。 单调性 导数的正负 函数及图象 x y o x y o 切线斜率 的正负 x y o 函数单调性与导数的关系？ 函数单调性与导数正负的关系 注意： 应正确理解 “ 某个区间 ” 的含义， 它必是定义域内的某个区间。 1 ．应用导数求函数的单调区间 ( 选填 :“ 增” ,“ 减” ,“ 既不是增函数 , 也不是减函数” ) (1) 函数 y=x － 3 在 [ － 3 ， 5] 上为 __________ 函数。 (2) 函数 y = x 2 － 3x 在 [2 ， +∞) 上为 _____ 函数， 在 ( － ∞ ,1] 上为 ______ 函数，在 [1,2] 上为 __ __________________________________ 函数。 基础训练： 应用举例 增 增 减 既不是增函数 , 也不是减函数 求函数 的单调区间。 例 1 变 1 ： 求函数 的单调区间。 理解训练： 解 ： 的单调递增区间为 单调递减区间为 解 ： 的单调递增区间为 单调递减区间为 变 3 ： 求函数 的单调区间。 变 2 ： 求函数 的单调区间。 巩固提高： 解 : 解 : 例 2 、已知导函数 的下列信息： 当 1< x <4 时， 当 x >4, 或 x <1 时， 当 x =4, 或 x =1 时， 试画出函数 f ( x ) 图象的大致形状。 4 1 解：由题意可知 当 1< x <4 时， f ( x ) 为增函数 当 x >4, 或 x <1 时， f ( x ) 为减函数 当 x =4, 或 x =1 时， 两点为“临界点” 其图象的大致形状如图。 例 3 、判断下列函数的单调性，并求出 单调区间： (1) f ( x )= x 3 +3 x ; 解： =3 x 2 +3=3( x 2 +1)>0 从而函数 f ( x )= x 3 +3 x 在 x ∈ R 上单调递增， 见右图。 (2) f ( x )= x 2 - 2 x - 3 ; 解： =2 x - 2=2( x - 1)>0 图象见右图。 当 >0 ，即 x >1 时，函数单调递增； 当 <0 ，即 x <1 时， 函数单调递减； (3) f ( x )=sin x - x ; x ∈(0, p) 解： =cos x - 1<0 从而函数 f ( x )=sin x - x 在 x ∈(0,  ) 单调递减， 见右图。 (4) f ( x )=2 x 3 +3 x 2 - 24 x + 1 ; 解： =6 x 2 + 6 x - 24=6( x 2 + x - 4)>0 当 >0 ， 即 时， 函数单调递增； 图象见右图。 当 <0 ， 即 时， 函数单调递减； 总结 : 当遇到三次或三次以上的 , 或图象很难 画出的函数求单调性问题时，应考虑导数法。 纳 ① 求定义域 ② 求 ③ 令 ④ 求定义域 1° 什么情况下，用“导数法” 求函数单调性、 单调区间较简便？ 2° 试总结用“导数法” 求单调区间的步骤？ 归 高 考 试 (04 年全国理 ) B x y o 尝 x y o 1 2 x y o 1 2 x y o 1 2 x y o 1 2 x y o 2 (A) (B) (C) (D) C 高 考 试 尝 设 是函数 的导函数， 的图象如 右图所示 , 则 的图象最有可能的是 ( ) 例 3 、如图，水以常速 ( 即单位时间内注入水的体积相同 ) 注入下面四种底面积相同的容器中，请分别找出与各容器对应的水的高度 h 与时间 t 的函数关系图象。 通过这堂课的研究，你明确了         ， 你的收获与感受是                         ， 你存在的疑惑之处有                  。 课堂小结