江苏省七市2020届高三第三次调研考试（6月） 数学 16页

‎2020届高三模拟考试试卷 数　　学 ‎ ‎(满分160分，考试时间120分钟)‎ ‎2020．6‎ 参考公式：‎ 柱体的体积公式：V柱体＝Sh，其中S为柱体的底面积，h为高．‎ 锥体的体积公式：V锥体＝Sh，其中S为锥体的底面积，h为高．‎ 一、 填空题：本大题共14小题，每小题5分，共70分．‎ ‎1. 已知集合A＝{－1，0，1}，B＝{0，2}，则A∪B＝________．‎ ‎2. 设复数z满足(3－i)z＝，其中i为虚数单位，则z的模是________．‎ ‎3. 如图是一个算法流程图，则输出k的值是________．‎ ‎4. 某校高一、高二、高三年级的学生人数之比为4∶4∶3.为了解学生对防震减灾知识的掌握情况，现采用分层抽样的方法抽取n名学生进行问卷检测．若高一年级抽取了20名学生，则n的值是________．‎ ‎5. 今年我国中医药选出的“三药三方”对治疗新冠肺炎均有显著效果，功不可没．“三药”分别为金花清感颗粒、连花清瘟胶囊、血必净注射液；“三方”分别为清肺排毒汤、化湿败毒方、宜肺败毒方．若某医生从“三药三方”中随机选出2种，则恰好选出1药1方的概率是________．‎ ‎6. 在平面直角坐标系xOy中，已知抛物线y2＝4x的准线是双曲线－＝1(a＞0)的左准线，则实数a的值是________．‎ ‎7. 已知cos(α＋β)＝，sin β＝，α，β均为锐角，则sin α的值是________．‎ ‎8. 公园里设置了一些石凳供游客休息，这些石凳是经过正方体各棱的中点截去8个一样 的四面体得到的(如图)．设石凳的体积为V1，正方体的体积为V2，则的值是________．‎ ‎9. 已知x＞1，y＞1，xy＝10，则＋的最小值是________．‎ ‎10. 已知等比数列{an}的前n项和为Sn.若4S2，S4，－2S3成等差数列，且a2＋a3＝2，则a6的值是________．‎ ‎11. 海伦(Heron，约公元1世纪)是古希腊亚历山大时期的数学家，以他的名字命名的“海伦公式”是几何学中的著名公式，它给出了利用三角形的三边长a，b，c计算其面积的公式S△ABC＝，其中p＝.若a＝5，b＝6，c＝7，则借助“海伦公式”可求得△ABC的内切圆的半径r的值是________．‎ ‎12. 如图，△ABC为等边三角形，分别延长BA，CB，AC到点D，E，F，使得AD＝BE＝CF.若＝2，且DE＝，则·的值是________．‎ ‎13. 已知函数f(x)＝若函数g(x)＝f(－x)＋f(x)有且仅有四个不同的零点，则实数k的取值范围是________．‎ ‎14. 在平面直角坐标系xOy中，过点P(2，－6)作直线交圆O：x2＋y2＝16于A，B两点， C(x0，y0)为弦AB的中点，则的取值范围是________．‎ 二、 解答题：本大题共6小题，共90分. 解答时应写出必要的文字说明、证明过程或演算步骤．‎ ‎15. (本小题满分14分)‎ 在△ABC中，角A，B，C所对的边分别为a，b，c.若＝.‎ ‎(1) 求cos C的值；‎ ‎(2) 若A＝C，求sin B的值．‎ ‎16. 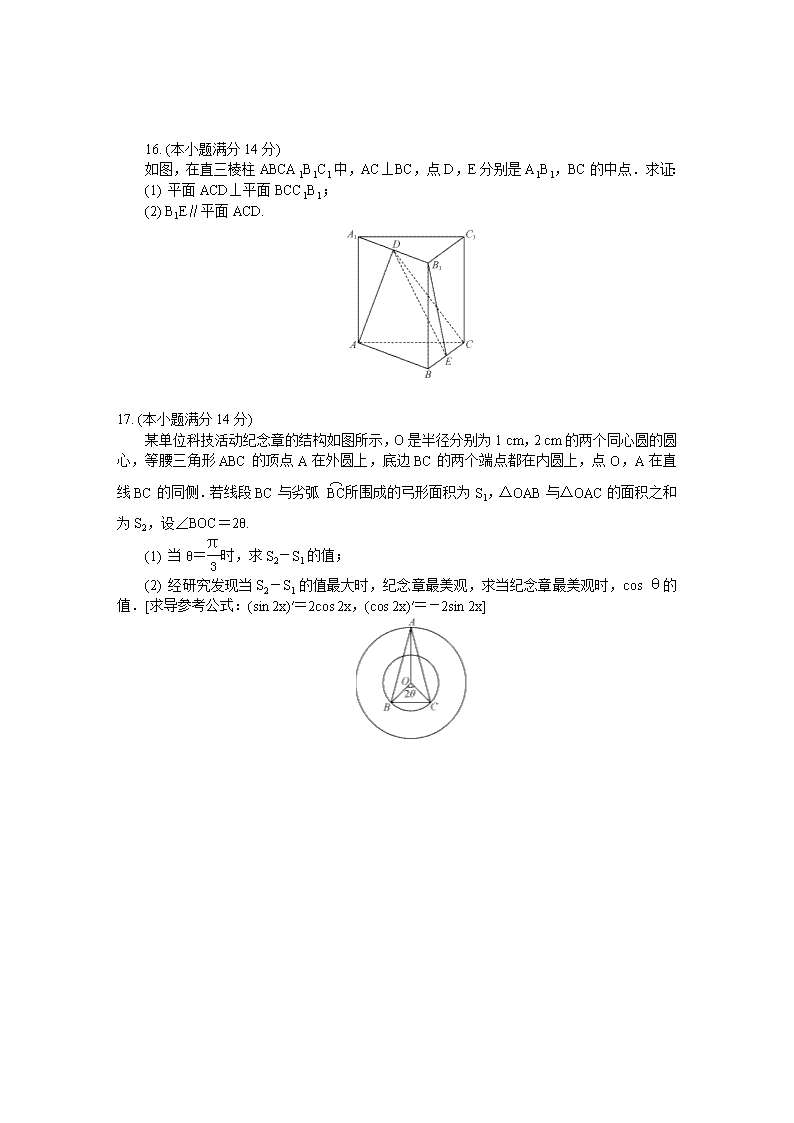(本小题满分14分)‎ 如图，在直三棱柱ABCA1B1C1中，AC⊥BC，点D，E分别是A1B1，BC的中点．求证：‎ ‎(1) 平面ACD⊥平面BCC1B1；‎ ‎(2) B1E∥平面ACD.‎ ‎17. (本小题满分14分)‎ 某单位科技活动纪念章的结构如图所示，O是半径分别为1 cm，2 cm的两个同心圆的圆心，等腰三角形ABC的顶点A在外圆上，底边BC的两个端点都在内圆上，点O，A在直线BC的同侧．若线段BC与劣弧 所围成的弓形面积为S1，△OAB与△OAC的面积之和为S2，设∠BOC＝2θ.‎ ‎(1) 当θ＝时，求S2－S1的值；‎ ‎(2) 经研究发现当S2－S1的值最大时，纪念章最美观，求当纪念章最美观时，cos θ的值．[求导参考公式：(sin 2x)′＝2cos 2x，(cos 2x)′＝－2sin 2x]‎ ‎18. (本小题满分16分)‎ 如图，在平面直角坐标系xOy中，已知椭圆＋＝1(a＞b＞0)的左、右焦点分别为F1，F2，过点F2的直线交椭圆于M，N两点．已知椭圆的短轴长为2，离心率为.‎ ‎(1) 求椭圆的标准方程；‎ ‎(2) 当直线MN的斜率为 时，求F1M＋F1N的值；‎ ‎(3) 若以MN为直径的圆与x轴相交的右交点为P(t，0)，求实数t的取值范围．‎ ‎19. (本小题满分16分)‎ 已知{an}是各项均为正数的无穷数列，数列{bn}满足bn＝an·an＋k(n∈N*)，其中常数k 为正整数．‎ ‎(1) 设数列{an}前n项的积Tn＝2，当k＝2时，求数列{bn}的通项公式；‎ ‎(2) 若{an}是首项为1，公差d为整数的等差数列，且b2－b1＝4，求数列的前2 020 项的和；‎ ‎(3) 若{bn}是等比数列，且对于任意的n∈N*，an·an＋2k＝a，其中k≥2，试问：{an}是等比数列吗？请证明你的结论．‎ ‎20. (本小题满分16分)‎ 已知函数f(x)＝，g(x)＝，其中e是自然对数的底数．‎ ‎(1) 若函数f(x)的极大值为，求实数a的值；‎ ‎(2) 当a＝e时，若曲线y＝f(x)与y＝g(x)在x＝x0处的切线互相垂直，求x0的值；‎ ‎(3) 设函数h(x)＝g(x)－f(x)，若h(x)＞0对任意的x∈(0，1)恒成立，求实数a的取值范围．‎ ‎2020届高三模拟考试试卷 数学附加题 ‎(满分40分，考试时间30分钟)‎ ‎21. 【选做题】 在A，B，C三小题中只能选做两题，每小题10分，共20分．若多做，则按作答的前两题计分．解答时应写出必要的文字说明、证明过程或演算步骤．‎ A. (选修42：矩阵与变换)‎ 已知m∈R，α＝是矩阵M＝的一个特征向量，求M的逆矩阵M－1.‎ B. (选修44：坐标系与参数方程)‎ 在极坐标系中，圆C的方程为ρ＝2rsin θ(r＞0)．以极点为坐标原点，极轴为x轴正半轴建立平面直角坐标系，直线l的参数方程为(t为参数)．若直线l与圆C恒有公共点，求r的取值范围．‎ C. (选修45：不等式选讲)‎ 已知x＞1，y＞1，且x＋y＝4，求证：＋≥8.‎ ‎【必做题】 第22，23题，每小题10分，共20分．解答时应写出必要的文字说明、证明过程或演算步骤．‎ ‎22. 某“芝麻开门”娱乐活动中，共有5扇门，游戏者根据规则开门，并根据打开门的数量获取相应奖励．已知开每扇门相互独立，且规则相同．开每扇门的规则是：从给定的6把钥匙(其中有且只有1把钥匙能打开门)中，随机地逐把抽取钥匙进行试开，钥匙使用后不放回．若门被打开，则转为开下一扇门；若连续4次未能打开，则放弃这扇门，转为开下一扇门；直至5扇门都进行了试开，活动结束．‎ ‎(1) 设随机变量X为试开第一扇门所用的钥匙数，求X的分布列及数学期望E(X)；‎ ‎(2) 求恰好成功打开4扇门的概率．‎ ‎23. 如图，在平面直角坐标系xOy中，已知抛物线y2＝2px(p＞0)的焦点为F，准线与x轴的交点为E.过点F的直线与抛物线相交于A，B两点，EA，EB分别与y轴相交于M，N两点．当AB⊥x轴时，EA＝2.‎ ‎(1) 求抛物线的方程；‎ ‎(2) 设△EAB的面积为S1，△EMN的面积为S2，求 的取值范围．‎ ‎2020届高三模拟考试试卷(南通、扬州、泰州等七市)‎ 数学参考答案及评分标准 ‎1. {－1，0，1，2}　2. 1　3. 5　4. 55　5. 　6. 　7. 　8. 　9. 9　10. －32　11. ‎12. －　13. (27，＋∞)　14. [，)‎ ‎15. 解：(1) 在△ABC中，因为＝，‎ 所以由正弦定理＝＝，得5(b＋c)(c－b)＝a(5a－8b)，‎ 即a2＋b2－c2＝ab，(4分)‎ 所以由余弦定理得cos C＝＝.(7分)‎ ‎(2) 因为cos C＝，C∈(0，π)，所以sin C＝＝，(9分)‎ 所以sin 2C＝2sin Ccos C＝.(12分)‎ 因为A＝C，所以sin B＝sin(π－A－C)＝sin(A＋C)＝sin 2C＝.(14分)‎ 注：(1) 正弦定理与＝＝，写一个不扣分，两者都不写，扣2分；余弦定理同样；‎ ‎(2) 只要有sin B＝sin(A＋C)，就不扣分，否则扣2分．‎ ‎16. 证明：(1) 在直三棱柱ABCA1B1C1中，CC1⊥平面ABC.‎ 因为AC⊂平面ABC，所以CC1⊥AC.(2分)‎ 因为AC⊥BC，BC∩CC1＝C，BC，CC1⊂平面BCC1B1，‎ 所以AC⊥平面BCC1B1.(4分)‎ 因为AC⊂平面ACD，‎ 所以平面ACD⊥平面BCC1B1.(6分)‎ ‎(2) (证法1)取AC的中点F，连结DF，EF.‎ 因为在△ABC中，点E是BC的中点，点F是AC的中点，‎ 所以EF∥AB，且EF＝AB.(8分)‎ 因为点D是A1B1的中点，所以B1D＝A1B1.‎ 因为在棱柱ABCA1B1C1中，AB∥A1B1，且AB＝A1B1，‎ 所以EF∥DB1，且EF＝DB1，(10分)‎ 所以四边形EFDB1是平行四边形，所以B1E∥FD.(12分)‎ 因为B1E⊄平面ADC，FD⊂平面ADC，‎ 所以B1E∥平面ACD.(14分)‎ ‎(证法2)取AB的中点G，连结EG，B1G.‎ 因为在△ABC中，点E是BC的中点，点G是AB的中点，‎ 所以EG∥AC.‎ 因为GE⊄平面ACD，AC⊂平面ACD，‎ 所以EG∥平面ACD.(8分)‎ 在棱柱ABCA1B1C1中，AB∥A1B1，且AB＝A1B1.‎ 因为点D是A1B1的中点，点G是AB的中点，‎ 所以AG∥DB1，且AG＝DB1，‎ 所以四边形AGB1D是平行四边形，所以B1G∥AD.‎ 因为B1G⊄平面ACD，AC⊂平面ACD，‎ 所以B1G∥平面ACD.(10分)‎ 因为EG∥平面ACD，BG，GE⊂平面B1GE，B1G∩GE＝G，‎ 所以平面B1GE∥平面ACD.(12分)‎ 因为B1E⊂平面B1GE，‎ 所以B1E∥平面ACD.(14分)‎ 注：少一个条件2分全扣；(1)中没有“在直三棱柱ABCA1B1C1中”全扣．‎ ‎17. 解：过点O作OD⊥BC于点D，则点D为BC的中点．‎ 又△ABC为等腰三角形，所以A，O，D三点共线，‎ 所以∠AOB＝∠AOC＝π－θ.‎ 所以S1＝×2θ×12－×12×sin 2θ＝θ－sin 2θ，(2分)‎ S2＝2××1×2sin(π－θ)＝2sin θ，θ∈(0，)．(4分)‎ 注：只要有S1结果的就给2分；同样，只要有S2结果的就给2分．‎ ‎(1) 当θ＝时，S2－S1＝2sin θ－(θ－sin 2θ)＝2sin －(－sin )＝－.‎ 答：当θ＝时，S2－S1的值为(－)cm2.(6分)‎ ‎(2) 设f(θ)＝S2－S1＝2sin θ－θ＋sin 2θ，θ∈(0，)，‎ 所以f′(θ)＝2cos θ－1＋cos 2θ＝2(cos2θ＋cos θ－1)．(8分)‎ 令f′(θ)＝0，得cos θ＝，cos θ＝(舍去)，‎ 记cos θ0＝，0<θ0<.(10分)‎ θ ‎(0，θ0)‎ θ0‎ ‎(θ0，)‎ f′(θ)‎ ‎＋‎ ‎0‎ ‎－‎ f(θ)‎ 极大值 所以当cos θ0＝时，f(θ)取得最大值，此时S2－S1的值最大．‎ 答：当纪念章最美观时，cos θ＝.(14分)‎ 注：一个答案1分，写成“所以”不扣分；答案中没有单位cm2的，扣1分．‎ ‎18. 解：(1) 设椭圆的焦距2c，由解得a2＝6，b2＝2，c2＝4.‎ 所以椭圆的标准方程为 ＋＝1.(3分)‎ ‎(2) 因为直线MN的斜率为，且过点F2(2，0)，所以直线MN的方程为y＝(x－2)．‎ 由得8x2－30x＋27＝0，解得x＝，x＝.‎ 所以M(，－)，N(，)，‎ 所以MN＝＝.(6分)‎ 因为(MF1＋MF2)＋(NF1＋NF2)＝MF1＋NF＋MN＝4，‎ 所以MF1＋NF1＝.(8分)‎ ‎(3) 设M(x1，y1)，N(x2，y2)．‎ 又P(t，0)，t>2，所以＝(x1－t，y1)，＝(x2－t，y2)．‎ 因为点P在以MN为直径的圆上，所以⊥，‎ 所以·＝(x1－t)(x2－t)＋y1y2＝0，‎ 所以x1x2－t(x1＋x2)＋t2＋y1y2＝0.(10分)‎ ‎①当直线MN倾斜角为0时，N(－，0)，M(，0)，所以t＝.‎ ‎②当直线MN倾斜角不为0时，设直线MN的方程为x＝my＋2.‎ 由消去x，得(m2＋3)y2＋4my－2＝0，‎ 所以 所以x1x2＝(my1＋2)(my2＋2)＝m2y1y2＋2m(y1＋y2)＋4，‎ x1＋x2＝m(y1＋y2)＋4.(12分)‎ 所以(m2＋1)y1y2＋(2m－tm)(y1＋y2)＋4－4t＋t2＝0，‎ 所以m2＝－≥0，(14分)‎ 解得0.‎ 由bn＝an·an＋k　①，bn＋k＝an＋k·an＋2k　②，‎ ‎②÷①得＝＝qk.‎ 因为an·an＋2k＝a，所以＝，即()2＝qk，所以＝q(正常数)．(12分)‎ 由bn＝an·an＋k　③，bn＋1＝an＋1·an＋k＋1　④，‎ ‎④÷③得＝·＝q　(*)．(14分)‎ 因为＝q，所以＝，将＝代入(*)式，得()2＝q，‎ 即＝q(正常数)，所以{an}为公比为q的等比数列．(16分)‎ ‎20. 解：(1) 因为f(x)＝，则f′(x)＝，(1分)‎ 令f′(x)＝0，得x＝e.因为a>0，列表如下：‎ x ‎(0，e)‎ e ‎(e，＋∞)‎ f′(x)‎ ‎＋‎ ‎0‎ ‎－‎ f(x)‎ 极大值 所以f(x)极大值＝f(e)＝＝，所以a＝1.(3分)‎ ‎(2) 当a＝e时，f(x)＝，则f′(x)＝，g(x)＝，则g′(x)＝.‎ 曲线y＝f(x)与y＝g(x)在x＝x0处的切线互相垂直，‎ 所以f′(x0)·g′(x0)＝－1，即·＝－1，(5分)‎ 整理得x0ex0＋eln x0－e＝0.‎ 设r(x)＝xex＋eln x－e，则r′(x)＝(x＋1)ex＋.‎ 因为x>0，所以r′(x)>0，‎ 所以r(x)＝xex＋eln x－e在(0，＋∞)上单调递增．(7分)‎ 因为r(1)＝0，且r(x0)＝0，所以x0＝1.(8分)‎ ‎(3) h(x)＝－，设m(x)＝ex－ex，则m′(x)＝ex－e.令m′(x)＝0，得x＝1.‎ 列表如下：‎ x ‎(－∞，1)‎ ‎1‎ ‎(1，＋∞)‎ m′(x)‎ ‎－‎ ‎0‎ ‎＋‎ m(x)‎ 极小值 所以m(x)最小值＝m(1)＝0.‎ 所以ex≥ex，所以ln ex≥ln ex，即x≥1＋ln x，即ln x≤x－1.(10分)‎ 注：主要出现上面一行内容，就给2分．‎ ‎① a≥时，ln a≥－1.因为0h(1)＝≥0.(14分)‎ ‎②当01，‎ 所以h(a)＝－ln a＝＋>>0.‎ 又h(x)在(0，1)上图象不间断，所以存在t∈(0，1)，使h(t)＝0，不合题意．‎ 综上，a的取值范围是[，＋∞)．(16分)‎ ‎2020届高三模拟考试试卷(二十)(南通、扬州、泰州等七市)‎ 数学附加题参考答案及评分标准 ‎21. A. 解：设α＝是矩阵M＝的一个特征向量，‎ 所以存在非零实数λ，使得Mα＝λα，‎ 所以＝λ，即解得，则M＝.(5分)‎ 设M－1＝，则MM－1＝E，即＝，所以 解得a＝－，b＝，c＝，d＝－，所以M－1＝.(10分)‎ B. 解：将直线l的参数方程为(t为参数)化为普通方程为x－y－2＝0.(3分)‎ 由ρ＝2rsin θ(r>0)，得ρ2＝2rρsin θ，‎ 所以圆C的直角坐标方程为x2＋(y－r)2＝r2.(6分)‎ 因为直线l与圆C恒有公共点，所以≤r，解得r≥2.‎ 所以实数r的取值范围是[2，＋∞)．(10分)‎ C. 证明：因为x>1，y>1，且x＋y＝4，由柯西不等式得 ‎(＋)[(x－1)＋(y－1)]≥(·＋·)2＝(x＋y)2＝16，(8分)‎ 即(＋)×2≥16，所以＋≥8.(10分)‎ ‎22. 解：(1) X的可能取值为1，2，3，4，P(X＝1)＝，‎ P(X＝2)＝×＝，P(X＝3)＝××＝，‎ P(X＝4)＝×××＋×××＝，(每个1分)‎ 所以X的分布列为 X ‎1‎ ‎2‎ ‎3‎ ‎4‎ P 所以随机变量X的数学期望E(X)＝1×＋2×＋3×＋4×＝3.(5分)‎ ‎(2) (解法1)记成功打开1扇门的事件为A，‎ 则P(A)＝＋＋＋×××＝.(8分)‎ 记恰好成功打开4扇门的事件为B，‎ 则P(B)＝C()4()＝.‎ 答：恰好成功打开4扇门的概率为.(10分)‎ ‎(解法2)记成功打开1扇门的事件为A，则P(A)＝1－×××＝.(8分)‎ 记恰好成功打开4扇门的事件为B，则P(B)＝C()4()＝.‎ 答：恰好成功打开4扇门的概率为.(答案不写扣1分)(10分)‎ ‎23. 解：(1) 当AB⊥x轴时，AF＝p，EF＝p，‎ 所以EA＝p＝2，即p＝，所以抛物线的方程为y2＝2x.(2分)‎ ‎(2) 设直线AB的方程为x＝my＋，由得y2－2my－2＝0.‎ 设A(x1，y1)，B(x2，y2)，所以y1＋y2＝2m，y1y2＝－2，‎ 则直线AE的方程为y＝(x＋)．‎ 令x＝0，得yM＝＝，同理yN＝＝，(4分)‎ 所以|yM－yN|＝＝，(6分)‎ 其中m2y1y2＋m(y1＋y2)＋2＝|－2m2＋4m2＋2|＝2m2＋2，‎ 则 ＝＝4m2＋4≥4，因此的取值范围是[4，＋∞)．(10分)‎