浙江省之江联盟2020届高三下学期4月开学考试数学试题 Word版含解析 23页

- 1 - 之江教育评价 2019 学年第二学期高三返校联考（2020.02） 数学试题卷 一、选择题（在每小题给出的四个选项中，只有一项是符合题目要求的） 1. 集合  3 10A x x   ，  2 7B x x   ，则 A B  （ ） A.  2 10x x  B.  2 7x x  C.  3 7x x  D.  3 10x x  【答案】C 【解析】 【分析】 由 A 与 B，找出两集合的交集即可． 【详解】∵ { | 3 10}A x x   ， 2 7{ | }B x x   ， ∴A∩B＝{ | 3 7}x x  ， 故选：C． 【点睛】本题考查了交集及其运算，熟练掌握交集的定义是解本题的关键，属于基础题． 2. 若函数 1( ) lnf x x a x    在区间 (1 )e， 上存在零点，则常数 a 的取值范围为（ ） A. 0 1a  B. 1 1a e   C. 1 1 1a e    D. 1 1 1a e    【答案】C 【解析】 【分析】 函数 f(x)在定义域内单调递增，由零点存在性定理可知    1 0, 0f f e  ，解不等式即可求得 a 的取值范围. 【详解】函数 1( ) lnf x x a x    在区间  1,e 上为增函数， ∵ (1) ln1 1 0f a    ， 1( ) ln 0f e e a e     ， 可得 1 1 1a e    故选：C． - 2 - 【点睛】本题主要考查了导数在函数零点存在性问题中的应用，对于零点存在性问题，有两 种思考方向：（1）直接利用导数研究函数单调性，结合零点存在性定理，讨论函数零点的情 况；（2）先将函数零点问题等价转化为两个函数图像的交点问题，再利用导数，并结合函数 图像讨论两函数交点情况，从而确定函数零点的情况. 3. “ 1x  ”是“ 2lg lg 0x x  ”成立的（ ） A. 充分不必要条件 B. 必要不充分条件 C. 充分必要条件 D. 既不充分也不必要条件 【答案】A 【解析】 【分析】 解出方程 2lg lg 0x x  的解，可以判断得出选项. 【详解】因为 2lg lg 0x x  ，所以 lg 0x  或 lg 1x  ，解得 1x  或 10x  ， 所以由“ 1x  ”可以推出“ 2lg lg 0x x  ”成立； 但由“ 2lg lg 0x x  ”不能推出“ 1x  ”， 所以“ 1x  ”是“ 2lg lg 0x x  ”成立的充 分不必要条件. 故选：A. 【点睛】本题考查充分条件与必要条件的判断、解对数方程，属于基础题. 4. 已知实数 x， y满足 3 4 3, 3 0, 0, x y y x y         则 2z x y  的最小值为（ ） A. 3 B. 9 7 C. 3 D. 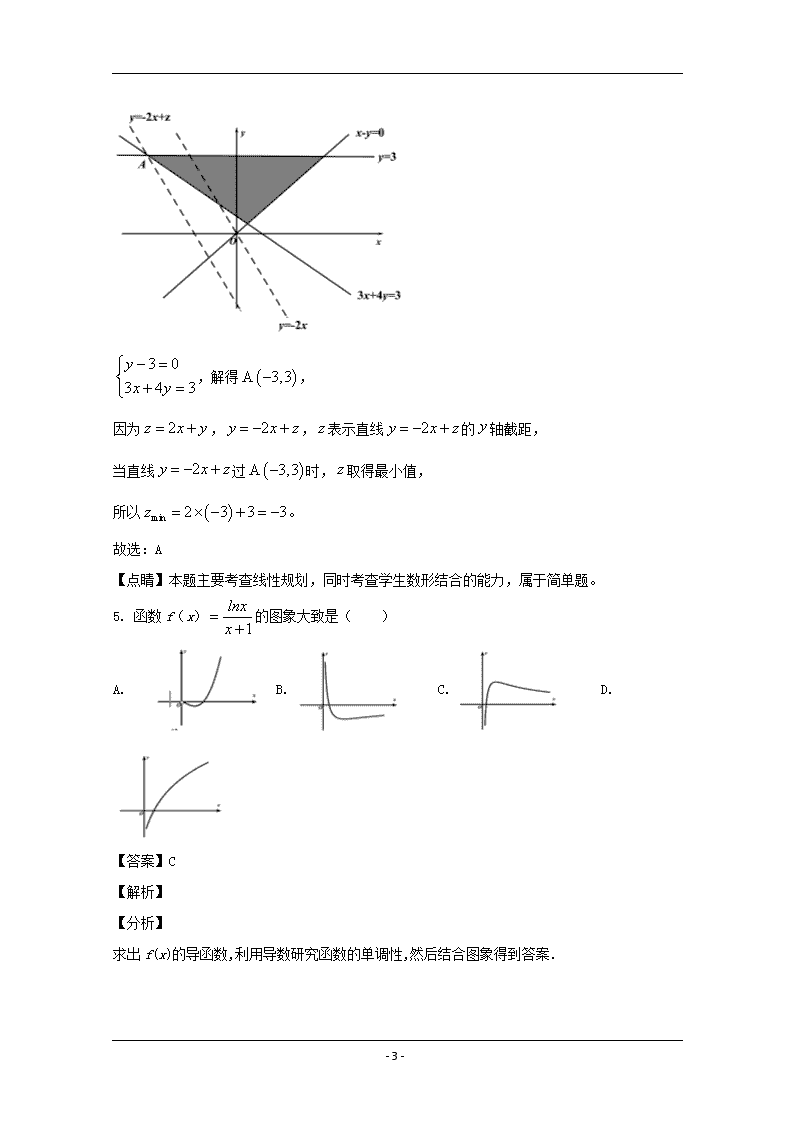9 【答案】A 【解析】 【分析】 首先根据题意画出不等式组表示的可行域，再根据 z的几何意义即可得到 z的最小值。 【详解】可行域如图所示： - 3 - 3 0 3 4 3      y x y ，解得  A 3,3 ， 因为 2z x y  ， 2y x z   ， z表示直线 2y x z   的 y轴截距， 当直线 2y x z   过  A 3,3 时， z取得最小值， 所以  min 2 3 3 3     z 。 故选：A 【点睛】本题主要考查线性规划，同时考查学生数形结合的能力，属于简单题。 5. 函数 f（x） 1 lnx x   的图象大致是（ ） A. B. C. D. 【答案】C 【解析】 【分析】 求出 f(x)的导函数,利用导数研究函数的单调性,然后结合图象得到答案. - 4 - 【详解】解:由 f(x) 1 lnx x   ,得 f′(x) 2 11 ( 0) ( 1) lnx x x x      , 令 g(x)＝1 1 lnx x   ,则 g′(x) 2 2 1 1 1 x x x x       ＜0, 所以 g(x)在(0,+∞)上单调递减, 又 g(e) 1 e  ＞ 0,g(e2 ) 2 2 2 1 11 1lne e e      ＜0, 所以存在 x0∈(e,e2),使得 g(x0)＝0, 所以当 x∈(0,x0)时,g(x)＞0,f′(x)＞0; 当 x∈(x0,+∞)时,g(x)＜0,f′(x)＜0, 所以 f(x)在(0,x0)上单调递增,在(x0,+∞)上单调递减. 故选:C. 【点睛】本题考查了利用导数研究函数的单调性和零点存在定理,属中档题. 6. 已知 ABC 的内角 A，B，C的对边分别是 a，b，c，若 sin 2 sinb A c B ， 1cos 4 B  ， 3b  ，则 ABC 的面积为（ ） A. 9 15 B. 9 15 16 C. 3 15 16 D. 9 16 【答案】B 【解析】 【分析】 先由正弦定理得 2a c ，再由余弦定理得 ,a c，最后由 1 sin 2 S ac B 求面积. 【详解】由 sin 2 sinb A c B 结合正弦定理可得 2ab bc ，则 2a c . 由余弦定理 2 2 2 2 cosb a c ac B   ，可得  2 2 19= 2 2 2 4 c c c c     ， 解得 3 2 c  ，则 3a  . 又 2 15sin 1 cos 4 B B   ， 所以 1 1 3 15 9 15sin 3 2 2 2 4 16ABCS ac B     △ . 故选：B. - 5 - 【点睛】本题考查由正弦定理、余弦定理解三角形，求三角形的面积.已知关于三角形的边和 角的正弦值的等式，一般由正弦定理化角为边或化边为角.已知角的余弦值，一般可由余弦定 理列式，属于中档题. 7. 国际象棋比赛中规定，胜方得1分，负方得 0分，和棋得0.5分.2019年浙江省青少年国际 象棋公开赛中，某选手每场比赛得分的分布列如下： X 1 0.5 0 P a b c 且 1 2 8 a b   ，则该选手进行一场比赛得分的期望一定不可能的是（ ） A. 0.3 B. 0.5 C. 0.7 D. 0.8 【答案】A 【解析】 【分析】 计算出随机变量 X 的数学期望为   1 2 E X a b  ，将代数式 1 2 a + b与 1 2 a b  相乘，展开后 利用基本不等式求得 1 2 a + b的最小值，进而可得出结果. 【详解】由随机变量 X 的分布列可知，随机变量 X 的数学期望为   1 2 E X a b  ， 易知0 1a  ，0 1b  ， 1 1 2 1 2 28 2 2 2 4 2 2 2 2 a b a ba b a b a b b a b a                          ， 即 1 4 1 2 8 2 a b   ，当且仅当 2b a 时，等号成立， 因此，该选手进行一场比赛得分的期望一定不可能的是0.3. 故选：A. 【点睛】本题考查离散型随机变量数学期望的求解，同时也考查了利用基本不等式求代数式 的最值，考查计算能力，属于中等题. 8. 四面体 ABCD中， 3AB CD  ，其余棱长均为 4，E，F 分别为 AB，CD上的点（不 含端点），则（ ） - 6 - A. 不存在 E，使得 EF CD B. 存在 E，使得DE CD C. 存在 E，使得DE 平面 ABC D. 存在 E， F ，使得平面CDE 平面 ABF 【答案】D 【解析】 【分析】 对于 A 选项，取 E，F分别在 AB，CD 的中点 ' ',E F 时，由全等三角形和等腰三角形的性质可判 断； 对于 D 选项，由 A选项的解析得 EF CD ， AF CD ，根据线面垂直和面面垂直的判定理 可判断； 对于 B 选项，作CH 面 ABD于H ，根据线面角的定义和最小角定理可得出 CDE 的最小 值和最大值可判断； 对于 C 选项，作DG 面 ABC于G，由点 G的位置和过空间中一点有且只有一条直线与已 知平面垂直，可判断. 【详解】作出示意图如下图所示： ' ',E F 分别是 AB，CD 的中点，CH 面 ABD于H ，DG  面 ABC于G， 对于 A 选项，取 E，F 分别在 AB，CD 的中点 ' ',E F 时，因为 3AB CD  ，其余棱长均为 4， 所以 ABC ABDV V ， 所以 ' 'CE DE ，所以 ' 'E F CD ，即 EF CD ，故 A错误； 对于 D 选项，取 E，F 分别在 AB，CD 的中点 ' ',E F 时，由 A 选项的解析得 ' 'E F CD ， 'AF CD ， ' ' ' 'E F AF F ， 所以CD 面 'ABF ，又CD面 'ECD，所以平面 'CDE 平面 'ABF ，即平面 CDE 平 面 ABF ，故 D 正确； 对于 B 选项，作CH 面 ABD于H ，因为 ABD△ 中， 4AD BD  ，所以H 定在 AB 的 中线 'DE 上， 所以 'CDE 就是CD与面 ABD所成的角， - 7 - 当 E 在 AB 上移动时， CDE 的最小值为直线CD与平面 ABD所成的角，即 'CDE ，而 'CDE 是锐角， CDE 的最大值为 2 CDB CDA      ， 故当 E 在 AB 上移动时，不存在 E，使得 DE⊥CD.故 B 错误. 对于 C 选项，作DG 面 ABC于G，因为 ABC 中， 4AC BC  ， 所以G定在 AB 的中线 'CE 上，且不重合于点 'E ，即点 G不落在 AB 上， 又因为过空间中一点有且只有一条直线与已知平面垂直，故不存在 E，使得 DE⊥平面 ABC， 故 C 选项不正确， 故选：D. 【点睛】本题考查空间的线线垂直、线面垂直、面面垂直、线面角的应用等综合动点问题， 属于较难题. 9. 已知动点 A， B关于坐标原点O对称， 2AB  ， M 过点 A， B且与直线 1y  相切. 若存在定点 P，使得 MA MP 为定值，则点 P的坐标为（ ） A. 10, 2       B. 10, 2      C.  0,1 D.  0, 1 【答案】B 【解析】 【分析】 根据圆的几何性质，结合圆的切线性质、勾股定理，通过计算可以判断出点M 的轨迹是抛物 线，再根据抛物线的定义进行求解即可. 【详解】设 ( , )M x y ，因为点 ,A B关于坐标原点O对称，所以O是线段 AB的中点， 又因为以M 为圆心的圆过 ,A B两点，所以有OA OM ， - 8 - 因此有 2 2 2OM OA MA  ，因为点 ,A B关于坐标原点O对称， 2AB  ，所以 1OA  . 又因为以M 为圆心的圆与直线 1y  相切，所以有 1MA y  ， 把 1OA  、 1MA y  代入 2 2 2OM OA MA  中，得： 22 2 1 1x y y    ，化简得： 2 2 ( 0)x y y   ，因此点M 的轨迹是抛物线， 该抛物线的焦点坐标为 1(0, ) 2 F  ，准线方程为： 1 2 y  ， 1 1 1 11 1 2 2 2 2 MA MP y MP y MP y MP y MP               ， 由抛物线的定义可知： 1 2 y MF  ， 所以有 1 2 MA MP MF MP    ， 由题意可知存在定点 P，使得当 A运动时， MA MP 为定值， 因此一定有 MF MP ，此时定点 P是该抛物线的焦点 1(0, ) 2 F  . 故选：B. 【点睛】本题考查了圆的切线性质，考查了圆的几何性质，考查了抛物线的判断，考查了抛 物线定义的应用，考查了数学运算能力，属于较难题. 10. 数列 na 满足 1 1 ,0 2 a       ，且   1 ln 1n n na a a n      N ，则（ ） A. 2 1 5 a  ， 4 3 5 S  B. 2 1 5 a  ， 4 3 5 S  C. 2 1 5 a  ， 4 3 5 S  D. 2 1 5 a  ， 4 3 5 S  【答案】D 【解析】 【分析】 构造函数    ln 1f x x x   ，利用导数分析出该函数的单调性，由 1 1 ,0 2 a       可得出 2 10 5 a  ，进而可推导出 3 10 5 a  ， 4 10 5 a  ，由此可得出结论. - 9 - 【详解】令    ln 1f x x x   ，当 1 0 2 x   时，   11 0 1 1 xf x x x        ， 所以，函数    ln 1f x x x   在区间 1 ,0 2      上单调递减， 同理可知，函数    ln 1f x x x   在区间  0,  上单调递增， 1 1 ,0 2 a        ，且   1 ln 1n n na a a n      N ， 则  2 1 1 1 1ln 2 2 2 5 a f a f           ，且    2 1 0 0a f a f   ，即 2 10 5 a  ；  3 2 1 1 6 1ln 5 5 5 5 a f a f          ，且    3 2 0 0a f a f   ，即 3 10 5 a  ； 同理  4 3 10, 5 a f a       ，因此， 4 1 2 3 4 3 5 S a a a a     . 故选：D. 【点睛】本题考查递推公式的应用，考查利用导数求数列中相关项的取值范围，考查分析问 题和解决问题的能力，属于难题. 二、填空题 11. 若复数 3 2iz i   （ i为虚数单位），则复数 z的虚部为______； z  ______． 【答案】 (1). 3 (2). 13 【解析】 【分析】 首先化简复数 z得到 2 3z i   ，再求复数 z的虚部和模长即可. 【详解】   2 3 23 2 2 3       i iiz i i i ，所以复数 z的虚部为 3 .    2 22 3 = 13   z . 故答案为： 3 ； 13 【点睛】本题主要考查复数的运算，同时考查复数的虚部和模长，属于简单题. 12. 双曲线 2 2 1 4 8 x y   的焦距是______，离心率是______． - 10 - 【答案】 (1). 4 3 (2). 3 【解析】 【分析】 根据双曲线的几何性质，求得焦距和离心率. 【详解】依题意 2, 4 8 2 3a c    ，所以焦距 2 4 3c  ，离心率 2 3 3 2 ce a    . 故答案为：（1）4 3；（2） 3 . 【点睛】本小题主要考查双曲线的几何性质，属于基础题. 13. 《九章算术》是我国古代内容极为丰富的数学名著，它系统地总结了战国、秦、汉时期 的数学成就，书中将四个面都是直角三角形的三棱锥称之为“阳马”．若某“阳马”的三视 图如图所示（单位： cm），则该阳马的体积为______ 3cm ，最长的棱长为______cm． 【答案】 (1). 10 (2). 5 2 【解析】 【分析】 由三视图还原几何体如下图所示，根据三棱锥的体积公式和勾股定理可求得答案. 【详解】由三视图还原几何体如下图所示，则该阳马的体积为  31 14 5 3 10 3 2 V cm      ， 由勾股定理得 2 23 4 5AC    ， 2 23 5 34BD    ， 2 2 24 34 5 2AB BD AD     ， - 11 - 所以最长的棱长为  5 2AB cm ， 故答案为：（1）10；（2）5 2 . 【点睛】本题考查由三视图还原几何体，求得几何体的体积和棱长，属于基础题. 14. 若      5 66 0 1 5 61 1 1x a a x a x a x          ，则 0 1 2 3 4 5 6a a a a a a a       ______， 5a  ______． 【答案】 (1). 64 (2). 6 【解析】 【分析】 利用赋值法求第一个问题，观察可得  6 6[ 1 1]x x   ，再利用展开式的通项公式求得第二个 问题的结果. 【 详 解 】 令 2x  ， 得 0 1 2 3 4 5 6 62 a a a a a a a       ， 所 以 0 1 2 3 4 5 6 64a a a a a a a       ； 又  6 6[ 1 1]x x   =      5 6 0 1 5 61 1 1a a x a x a x      ，将 1x  视为一个整体，则 5a 为二项式展开式中  51x  的系数， 展开式的通项公式为 6 1 6 1) 1r r r rT C x    （ ，令 1r  ，则  51x  的系数的值为 1 1 6 61C   ， 故答案为：64，6. 【点睛】本题考查了二项式展开式定理的应用问题，考查了展开式中的通项公式的应用及赋 值法，属于基础题． 15. “2019 曹娥江国际马拉松”在上虞举行，现要选派 5 名志愿者服务于 , , ,A B C D四个不 - 12 - 同的运动员救助点，每个救助点至少分配 1 人，若志愿者甲要求不到 A 救助点，则不同的分 派方案有________种. 【答案】180 【解析】 【分析】 先对甲单独服务和甲与其他人一起服务分类计数，再考虑甲要求不到 A 救助点计算两类的方 法种数，求得不同的分派方案种数. 【详解】根据志愿者甲的特殊要求，应按甲单独服务、甲与其他人一起服务分类计数. 若甲单独服务，则甲有 3 种选法，其余各人先从另 4 人中选 2 人组团， 再分配给余下的 3 个救助点，共 2 3 4 3C A 种方法； 若甲与其他人组团服务，则从 4 人中选 1 人与甲组团，有 1 4C 种选法， 再定求助点有 1 3A 种方法，其余 3人救助点的选法有 3 3A 种， 故共有 2 3 1 1 3 4 3 4 3 33 180C A C A A  （种）方法. 故答案为：180 【点睛】本题考查排列组合与计数原理,合理分类，特殊元素和位置的考虑是解决问题的关键， 思路过程不清极易出现遗漏与重复计数的错误. 16. 已知平面向量 ,a b  满足 2a a b     ．对任意的 t R ，都有 2 3a tb b    成立，则 b  的取值范围是______． 【答案】 2 3[ , 2] 3 【解析】 【分析】 先设a与b  的夹角为  0    ， | | ( 0)b m m  r ，根据向量数量积的计算公式，以及向 量模的计算公式，结合题中条件，即可求出m的范围，得出结果． 【详解】设a与b  的夹角为  0    ， | | ( 0)b m m  r ， 所以 2 cos 2a b m    rr ，即 1cos [ 1,1] m     ，所以 1m  ． - 13 - 因为对任意的 tR ，都有 2 3a tb b    成立，所以对任意的 tR ，不等式 2 2 2 08 16 3m t t+ m   恒成立， 所以  2 2 0166 34 4m m   ，解得 24 3 4m  ， 所以 2 3[ , 2] 3 m ，即 b  的取值范围是 2 3[ , 2] 3 ． 故答案为： 2 3[ , 2] 3 ． 【点睛】本题主要考查平面向量的数量积、平面向量模的计算，属于中档题． 17. 已知函数   2 af x x t x    （10 20a  ，且aN ）在 1,4 上的最大值为  g t ，若  g t 的最小值为 4，则常数 a _______． 【答案】16 【解析】 【分析】 令   2 ah x x x   ，利用导数分析函数  y h x 在区间  1,4 上的单调性，可求得该函数在区 间 1,4 上的值域为 2 33 , 16 4 4 a a       ，进而可得   2 3max 16 , 3 4 4 a ag t t t           ，结合三 角不等式可得出 2 3 3 4 0 8 2 4 a a    ，进而可求得自然数 a的值. 【详解】令   2 ah x x x   ，则   3 2 2 22 a x ah x x x x     ，令   0h x  ，可得 3 2 ax  ， 10 20a  ，则  3 33 5, 10 1,4 2 a     ，所以  3 1,4 2 a  . 当 31 2 ax  时，   0h x  ，此时，函数  y h x 单调递减； 当 3 4 2 a x  时，   0h x  ，此时，函数  y h x 单调递增. - 14 - 所以，   2 33 min 3 2 4 a ah x h         ， 又  1 1h a  ，  4 16 4 ah   ，      3 31 4 15 20 0 4 4 ah h a      ，则    max 4 16 4 ah x h   . 所以，函数    f x h x t  的最大值为   22 33 2 3 16 316 3 4 44 4 max 16 , 3 4 4 2 2 a aa a t tt t a ag t t t                              2 316 3 4 4 4 2 a a     ， 设 3 33 5, 10 2 ar     ，则 2 3 3 2 16 3 4 4 1 6 32 4 2 4 a a r r       ， 令   3 26 32r r r    ，则    23 12 3 4 0r r r r r      ， 所以，函数  y r 在 3 35, 10r    上单调递减，则      3 3 310 42 6 100 6 7 100 0r       . 所以， 3 2 3 21 6 326 32 4 4 4 r rr r       ，整理得 3 26 16 0r r   ， 即   22 4 8 0r r r    ，由于 3 35, 10r    ，解得 2r = ，即 3 2 2 a  ，解得 16a  . 故答案为：16 . 【点睛】本题考查利用含绝对值函数在区间上的最值求参数，考查绝对值三角不等式以及导 数的应用，考查分析问题和解决问题的能力，属于难题. 三、简答题：解答应写出文字说明、证明过程或演算步骤. 18. 已知函数   sin cos 3 sin cos 2 f x x x x x       ． （1）求函数  f x 的单调递增区间； - 15 - （2）若  f x a 在区间 0, 2      上有两个不同的解 1x ， 2x ，求 a的范围及 1 2x x 的值． 【答案】（1） + , + ( ) 3 6 k k k Z       ；（2） a的范围为 10, 2     ， 1 2 3 x x    . 【解析】 【分析】 （1）直接利用三角函数关系式的恒等变换的应用，把函数的关系式变形成正弦型函数，进一 步求出函数的单调增区间． （2）利用函数的定义域求出函数的值域，进一步求出参数 a的范围和 1 2x x 的值． 【详解】解：（1）函数   sin cos 3 sin cos 2 f x x x x x       2 3 1 cos2 3 1sin sin 2 sin 2 sin 2 2 2 2 6 2 xx x x x               ． 由 +2 2 +2 ( ) 2 6 2 k x k k Z        ，解得 + + ( ) 3 6 k x k k Z      ， 所以函数  f x 的单调递增区间为： + , + ( ) 3 6 k k k Z       ． （2）由于0 2 x    ，所以 72 6 6 6 x      ，所以在 1 sin 2 1 2 6 x        时，  f x a 在 区间 0, 2      上有两个不同的解 1x ， 2x ， 故 a的范围为 10, 2     ． 又令 2 + ( ) 6 2 x k k Z     ，解得 + ( ) 6 2 kx k Z    ， 所以函数  f x 的图象在区间 0, 2      上关于 6 x   对称，故 1 2 2 6 3 x x       ， 所以 1 2 3 x x    ． 【点睛】本题考查三角函数关系式的恒等变换，正弦型函数的性质的应用，主要考查学生的 运算能力和转换能力及思维能力，属于中档题． - 16 - 19. 如图，四棱锥 S ABCD 中， //AD BC， AD AS ， 2AD  ， 2CD  ， 1AB BC AS   ， 2 3 SAB    ． （1）求证： AD BS ； （2）求直线CD与平面 SAC所成角的正弦值． 【答案】（1）证明见解析；（2） 42 7 . 【解析】 【分析】 （1）取 AD的中点E，连接CE，证明出四边形 ABCE为平行四边形，以及CE AD ，进 而可得出 AD AB ，结合 AD AS 可得出 AD平面 SAB，由此可得出 AD BS ； （2）以点 A为坐标原点， AB、 AD所在直线分别为 y、 z轴建立空间直角坐标系，利用空 间向量法可求得直线CD与平面 SAC所成角的正弦值. 【详解】（1）如下图所示，取 AD的中点 E，连接CE . 1BC  ， 2AD  ， E为 AD的中点，则 1 1 2 AE AD  ， BC AE  ， 又 //AD BC，可得 //BC AE，四边形 ABCE为平行四边形， //CE AB ， - 17 - 且 1DE  ， 1CE AB  ， 2CD  ， 2 2 2CE DE CD   ， 2 CED    ，则CE AD ， AD AB  ， AD AS ， AB AS A  ， AD 平面 SAB， BS  平面 SAB，因此， AD BS ； （2）以点 A为坐标原点， AB、 AD所在直线分别为 y、 z轴建立如下图所示的空间直角坐 标系 A xyz ， 则点  0,0,0A 、  0,1,1C 、  0,0,2D 、 3 1, ,0 2 2 S        ， 所以，  0, 1,1CD    ，  0,1,1AC   ， 3 1, ,0 2 2 AS          . 设平面 SAC的法向量为  , ,n x y z  ， 由 0 0 n AC n AS         ，得 0 3 1 0 2 2 y z x y       ，可得 3y x z y      ， 令 1x  ，可得 3y  ， 3z   ，则  1, 3, 3n    ， 2 3 42cos , 77 2 n CDn CD n CD              . 因此，直线CD与平面 SAC所成角的正弦值为 42 7 . 【点睛】本题考查利用线面垂直证明线线垂直，同时也考查了利用空间向量法求解线面角的 正弦值，考查推理能力与计算能力，属于中等题. - 18 - 20. 已知公差为 2 等差数列 na 的前 n 项和为 nS 满足 1S ， 2S ， 4S 成等比数列． （1）求数列 na 的通项公式； （2）证明；当 2n  时， 1 2 3 1 1 1 1 3 2 3 2na a a na       ． 【答案】（1） 2 1na n  ；（2）证明见解析. 【解析】 【分析】 （1）由等比数列的性质得 42 2 1S SS   ，代入可求得首项 1a ，从而得数列 na 的通项公式； （2）运用放缩法，当 2n  时， 1 1 1 1 1 (2 2) 2 1nna n n n n        ，可得证. 【详解】（1）因为 1S ， 2S ， 4S 成等比数列，所以 42 2 1S SS   ，即    2 1 1 12 +2 4 +6 2aa a   ， 解得 1 1a  ， 所以  1 1 2 2 1na n n      ， 所以数列 na 的通项公式为 2 1na n  ； （2）当 2n  时， 1 1 1 1 1 1 1 1 (2 1) (2 2) 2 ( 1) 2 1nna n n n n n n n n            ， 所以 1 2 3 1 1 1 1 1 1 1 1 1 1 3 1 31 1 2 3 2 2 2 3 1 2 2 2na a a na n n n                     ， 所以 1 2 3 1 1 1 1 3 2 3 2na a a na       . 【点睛】本题考查等差数列的基本量计算，以及运用放缩法和裂项求和法证明不等式，属于 中档题. 21. 已知椭圆 E : 2 2 2 2 1x y a b   （ 0a b  ）的离心率为 1 2 ，F 为其右焦点，直线 4x  上动 点 A到椭圆 E上点的距离的最小值为 2． - 19 - （1）求椭圆 E的方程； （2）线段 AF 交椭圆 E于点 B，直线 AC与椭圆E有且仅有一个公共点C．试证明 FA FC ，并求 FBC 面积的最小值． 【答案】（1） 2 2 1 4 3 x y   ；（2） 81 36 2 49  . 【解析】 【分析】 （1）由已知条件求得 , ,a b c，可得出椭圆的标准方程； （2）设点  0 0,C x y ，  4,A t ，  1,0F ，设过点 C 椭圆 E的切线方程为： y kx m  ，与 椭圆的方程联立，由根的判别式为 0 得出 , ,k m t的关系，进而表示出点 C 的坐标，由向量垂直 的条件FA FC 可得证，再设直线 BC 的方程 y kx m  ，由前面所证的结论 FA FC ，建 立关于 k，m 的关系，表示 FBC 的面积，运用函数知识，可求得 FBC 面积的最小值. 【详解】（1）由已知得 1 , 4 2 2 2 c a a     ，所以 2 2 21, 3c b a c    ，所以椭圆 E的方 程为 2 2 1 4 3 x y   ； （2）设点  0 0,C x y ，  4,A t ，  1,0F ，则过点 C 椭圆 E的切线方程为： y kx m  ，与 椭圆 E 的方程联立 2 2 1 4 3 y kx m x y       ，整理得  2 2 23+4 +8 +4 12 0kmk mxx   ，则       2 2 2 2 28 4 3+4 4 12 48 4 +3 0k mk k mm       ，所以 2 24 +3 0k m  ，即 2 24 +3m k ，解得 20 2 4 4 4 3+4k km km kx m m       ， - 20 - 因为点  4,A t 在切线上，所以 4t k m  ， 又    0 03 , 1,FA t FC x y     ， ， 所以        0 0 0 03 1 + 3 1 + 4 + +FA FC x ty x k m kx m              2 2 0 4+ +3+4 + 4 + 3 + 4 + 3kmk mkk x m k m m m m m k         2 24 4 +4 + 3 0km kmk m     ，所以FA FC   ，即 FA FC ； 直线 AF 的方程为：  1 3 ty x  ，与椭圆的方程联立   2 2 1 3 1 4 3 ty x x y         得   22 2 227+4 8 +4 108 0t xt x t   ，        2 2 2 228 4 27+4 4 108 16 81 +9t tt t        ， 设点 B 的坐标为  1 1,B x y ，且 1>0x ，则 2 1 2 2 4 +18 +9 27+4 t tx t      22 2 22 0 0 0 0 0 2 11 + 1 +3 1 2 4 2 xx y x xFC                ，所以 1 12 2 FC x  ，同理 2 12 2 FB x  ，    0 1 0 1 1 1 1 1 12 2 4 4 2 2 2 2 8FBCS FC FB x x x x                 2 2 2 2 2 2 1 4 4 +18 +9 2 +9 +94+ 4 1+ 2 8 27+4 27+4 k t t t t t t k m m                              2 2 2 +9 9 +9 1 27 4 6 + + k m t t t             ， 综上可得： FBC 面积的最小值为 81 36 2 49  . 【点睛】本题考查求椭圆的标准方程，直线与椭圆的位置之求三角形的面积的最值问题，关 键在于将三角形的面积表示成某个变量的函数，属于较难题. 22. 已知 0a  ，函数   ln xf x x  ， ( ) 1g x ax= - ． - 21 - （1）当 a为何值时，直线  y g x 是曲线  y f x 的切线； （2）是否存在实数 a，使得    g x a f ax  恒成立？若存在，求实数 a的取值集合；若不 存在，请说明理由． 【答案】（1） 1a  ；（2）存在， 1a  . 【解析】 【分析】 (1) 设切点为 0 0 0 ln xx x       ， ，设出切线方程为  0 0 0 0 2 0 ln 1 lnx xy x x x x    ，由  y g x 恒过  0 1， ，代入可求得 a的值. (2)    g x a f ax  恒成立，等价于  2 ln 0a x xx a   恒成立，构造函数    2 lnF x a x axx   ，需  min 0F x  ，从而可求得 a的取值. 【详解】（1）因为   ln xf x x  ，所以  ' 2 1 ln xf x x   ， 若直线  y g x 是曲线  y f x 的切线，设切点为 0 0 0 ln xx x       ， ，此时切线方程为  0 0 0 0 2 0 ln 1 lnx xy x x x x    ， 又  y g x 恒过  0 1， ，所以  2 0 0 0 0 0 ln 1 ln1 0x x x x x      ，即 0 02ln + 1 0x x   ， 令   2ln + 1h x x x  ，则  1 2ln1+1 1 0h    ，且  h x 在  0 ， 上单调递增， 所以方程 0 02ln + 1 0x x   有唯一的解 0 1x  ，所以  ' 0 2 1 l 1 1(1) n1f x af     ， 所以当 1a  时，直线  y g x 是曲线  y f x 的切线； （2）假设存在实数 a，使得    g x a f ax  恒成立，即  2 ln 0a x xx a   恒成立. 令    2 lnF x a x axx   ，则 2 ' 2 1( ) ax xF x x    ，令 2( ) 2 1G x ax x   ，又 0a  ，则 1 8 0a    ， 所以 ( ) 0G x  有两个不等根 1x ， 2x ， 1 2 1 0 2 x x a    ，不妨设 1 20x x  . - 22 - 所以  F x 在 2(0, )x 上递减，在  2 ,x  上递增.所以 2 2 2 2 2( ) ln( ) 0F x ax x ax    成立. 因为 2 2 2 2( ) 2 1 0G x ax x    ，所以 2 2 2 1 2 xax x   ，所以   2 2 2 2 1 1( ) ln 0 2 2 x xF x F x x       ． 令 1 1 1( ) ln ln 2 ln(1 ) 2 2 2 x x xH x x x x          ， ( 1)( 2)( ) 2 ( 1) x xH x x x       ， 所以 ' ( )H x 在 (0,1)有 '( )>0H x ，在 (1, ) 上有 '( ) 0H x  ，所以 ( )H x 在 (0,1)上递增，在 (1, ) 上递减.所以 ( ) (1) 0H x H  . 又   2 2 2 2 1 1ln 0 2 2 x xF x x      ，所以  2 0F x  ， 2 1x  . 代入 2 2 2 1 2 xax x   ，得 1a  ， 所以存在实数 a，使得    g x a f ax  恒成立，此时 1a  ． 【点睛】本题考查函数与导数的综合问题.由导数的几何意义求切线方程，恒成立问题一般可 转化为最值问题，属于较难题. - 23 -