高中数学：三-1《相似三角形的判定》教案6（新人教A版选修4-1） 3页

相似三角形的判定（一）‎ ‎〔教学目标〕‎ 1． 了解相似比的定义，掌握判定两个三角形相似的方法：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似；如果两个三角形的三组对应边的比相等，那么这两个三角形相似。‎ 2． 培养学生的观察﹑发现﹑比较﹑归纳能力，感受两个三角形相似的判定方法1与全等三角形判定方法（SSS）的区别与联系，体验事物间特殊与一般的关系。‎ 3． 让学生经历从实验探究到归纳证明的过程，发展学生的合情推理能力。‎ ‎〔教学重点与难点〕‎ 重点：两个三角形相似的判定引例﹑判定方法1 ‎ 难点：探究判定引例﹑判定方法1的过程 ‎〔教学设计〕‎ 教学过程 设计意图说明 新课引入：‎ 1． 复习相似多边形的定义及相似多边形相似比的定义 ‎↓‎ 相似三角形的定义及相似三角形相似比的定义 2． 回顾全等三角形的概念及判定方法（SSS）‎ ‎↓‎ 相似三角形的概念及判定相似三角形的思路。‎ 从相似多边形的概念及全等三角形的概念两个以旧引新，帮助学生建立新旧知识间的联系，体会事物间一般到特殊﹑特殊到一般的关系。‎ 提出问题：‎ 如图27·2-1，在∆ABC中，点D是边AB的中点，DE∥BC，‎ DE交AC于点E ，∆ADE与∆ABC有什么关系？‎ 分析：观察27·2-1易知AD=，AE=，∠A=∠A，∠ADE=∠ABC，∠AED=∠ACB，只需引导学生证得DE=即可，学生不难想到过E作EF∥AB。‎ ‎↓‎ ‎∆ADE∽∆ABC，相似比为。‎ 延伸问题：‎ 改变点D在AB上的位置，先让学生猜想∆ADE与∆‎ 通过观察特殊平行条件（经过三角形一边的中点平行于另一边）下两三角形的相似关系，引导学生思考一般平行条件（平行于三角形一边的直线和其他两边相交）下两三角形的相似关系，进一步体会事物间特殊到一般的关系。‎ ABC仍相似，然后再用几何画板演示验证。‎ ‎↓‎ 归纳：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。‎ 通过几何画板演示，培养学生的实验探究意识。‎ 探究方法：‎ 探究1‎ 在一张方格纸上任意画一个三角形，再画一个三角形，使它的各边长都是原来三角形各边长的k倍，度量这两个三角形的对应角，它们相等吗？这两个三角形相似吗？‎ 分析：学生通过度量，不难发现这两个三角形的对应角都相等，根据相似三角形的定义，这两个三角形相似。（学生小组交流）‎ 在学生小组交流的基础上引导学生思考证明探究所得结论的途径。‎ 分析：作A1D=AB，过D作DE∥B‎1C1，交A‎1C1于点E ‎∆A1DE∽∆A1B‎1C1。用几何画板演示∆ABC平移至∆A1DE的过程 ‎ A1D=AB，A1E=AC，DE=BC∆A1DE≌∆ABC ‎ ∆ABC∽∆A1B‎1C1‎ ‎↓‎ 归纳：如果两个三角形的三组对应边的比相等，那么这两个三角形相似。‎ ‎↓‎ ‎ 学生通过作图，动手度量三角形的各边长及三角形的角，在动手实践中 探究几何结论成立与否，加深了学生对定理的重发现体验。‎ 通过几何画板演示让学生从中体会到把不熟悉的几何问题（如果两个三角形的三组对应边的比相等，那么这两个三角形是否相似？）转化为熟悉的几何问题（平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似）的过程。‎ ‎ ‎ 对几何定理作文字语言﹑图形语言﹑符号语言的三维注解有利于学生进行认知重构，以全方位地准确把握定理的内容。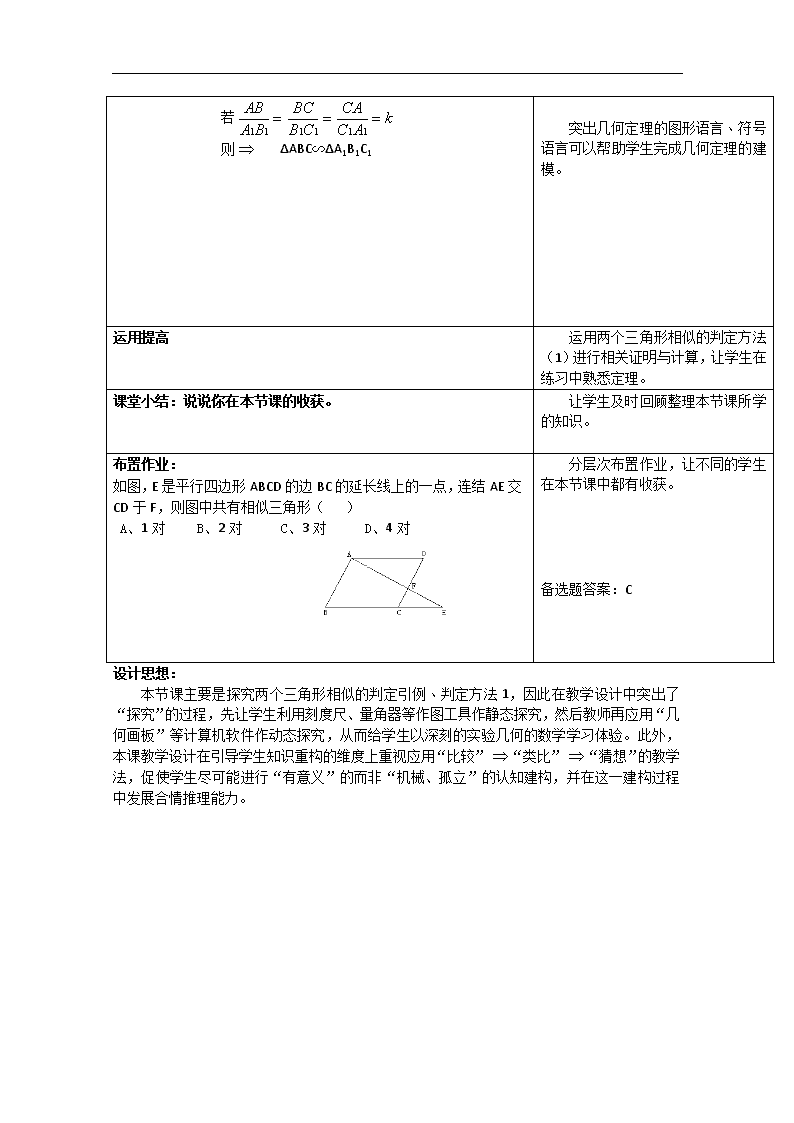‎ 若 则 ∆ABC∽∆A1B‎1C1‎ ‎ ‎ 突出几何定理的图形语言﹑符号语言可以帮助学生完成几何定理的建模。‎ 运用提高 运用两个三角形相似的判定方法（1）进行相关证明与计算，让学生在练习中熟悉定理。 ‎ 课堂小结：说说你在本节课的收获。‎ 让学生及时回顾整理本节课所学的知识。‎ 布置作业：‎ 如图，E是平行四边形ABCD的边BC的延长线上的一点，连结AE交CD于F，则图中共有相似三角形（ ）‎ ‎ A、1对 B、2对 C、3对 D、4对 分层次布置作业，让不同的学生在本节课中都有收获。‎ 备选题答案：C 设计思想：‎ ‎ 本节课主要是探究两个三角形相似的判定引例﹑判定方法1，因此在教学设计中突出了“探究”的过程，先让学生利用刻度尺、量角器等作图工具作静态探究，然后教师再应用“几何画板”等计算机软件作动态探究，从而给学生以深刻的实验几何的数学学习体验。此外，本课教学设计在引导学生知识重构的维度上重视应用“比较”“类比”“猜想”的教学法，促使学生尽可能进行“有意义”的而非“机械、孤立”的认知建构，并在这一建构过程中发展合情推理能力。‎ w.w.w.k.s.5.u.c.o.m ‎ www.ks5u.com