- 2.49 MB
- 2021-07-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
*第八章 立体几何
考点1 空间几何体的结构及其三视图与直观图
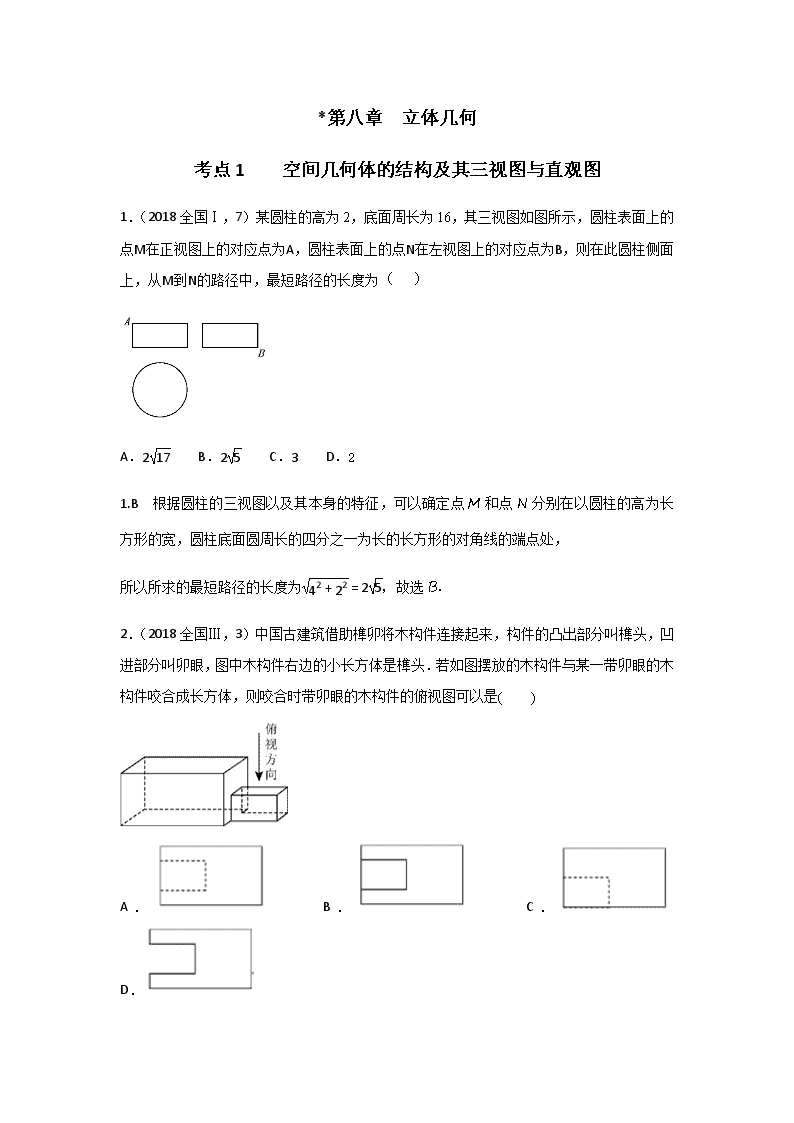
1.(2018全国Ⅰ,7)某圆柱的高为2,底面周长为16,其三视图如图所示,圆柱表面上的点M在正视图上的对应点为A,圆柱表面上的点N在左视图上的对应点为B,则在此圆柱侧面上,从M到N的路径中,最短路径的长度为( )
A.217 B.25 C.3 D.2
1.B 根据圆柱的三视图以及其本身的特征,可以确定点M和点N分别在以圆柱的高为长方形的宽,圆柱底面圆周长的四分之一为长的长方形的对角线的端点处,
所以所求的最短路径的长度为42+22=25,故选B.
2.(2018全国Ⅲ,3)中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )
A. B. C. D.
2.A 观擦图形图可知,俯视图为,故答案为A.
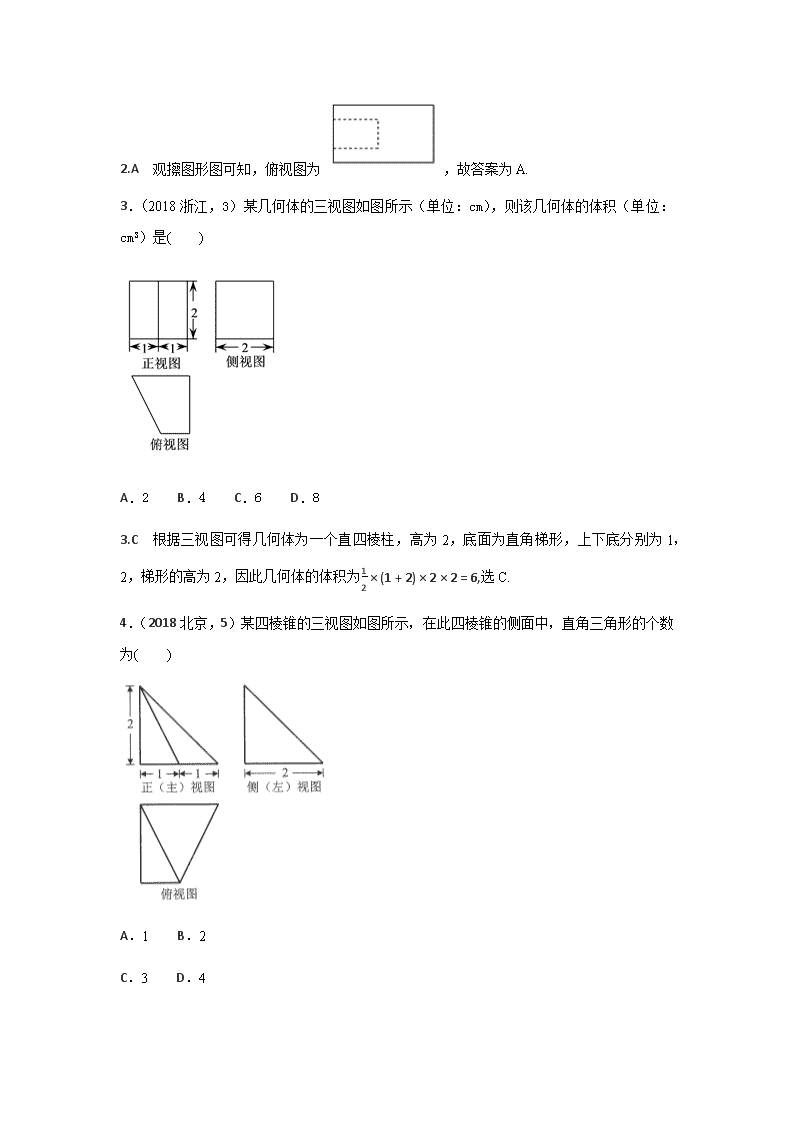
3.(2018浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是( )
A.2 B.4 C.6 D.8
3.C 根据三视图可得几何体为一个直四棱柱,高为2,底面为直角梯形,上下底分别为1,2,梯形的高为2,因此几何体的体积为12×(1+2)×2×2=6,选C.
4.(2018北京,5)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为( )
A.1 B.2
C.3 D.4
4.C 由三视图可得四棱锥P-ABCD,在四棱锥P-ABCD中,PD=2,AD=2,CD=2,AB=1,
由勾股定理可知:PA=22,PC=22,PB=3,BC=5,则在四棱锥中,直角三角形有:ΔPAD,ΔPCD,ΔPAB共三个,故选C.
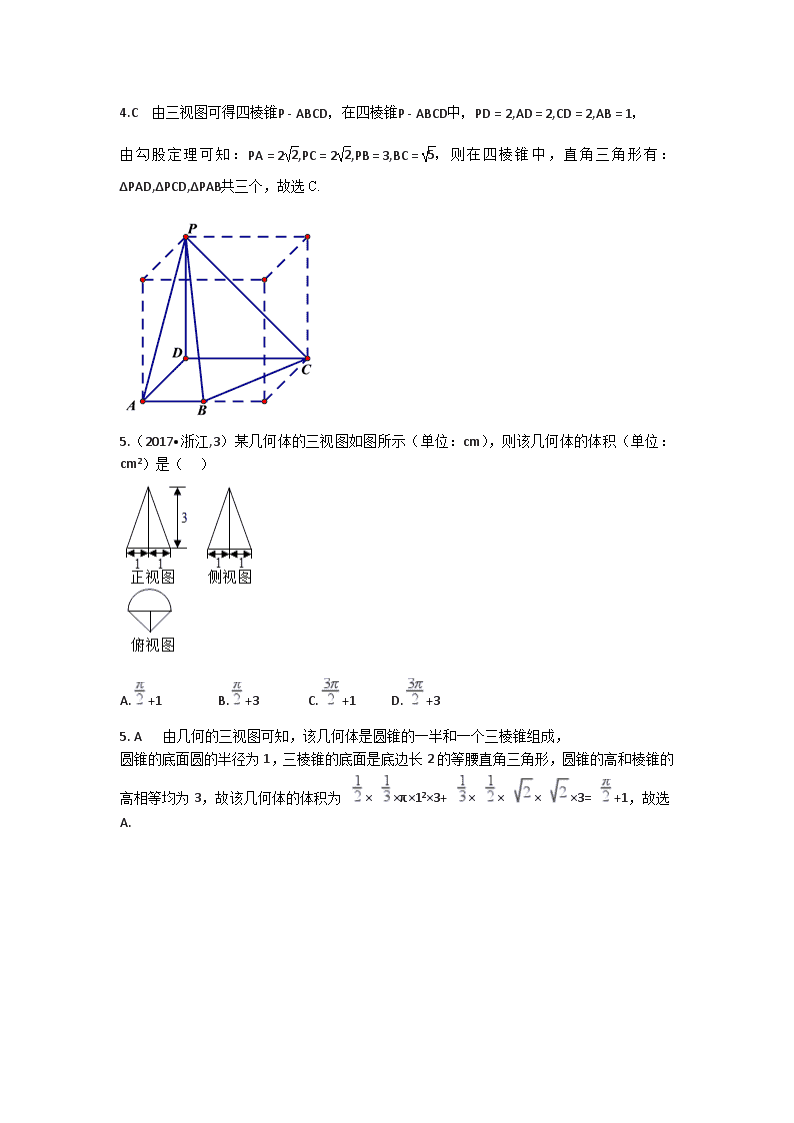
5.(2017•浙江,3)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm2)是( )
A.+1 B.+3 C.+1 D.+3
5. A 由几何的三视图可知,该几何体是圆锥的一半和一个三棱锥组成,
圆锥的底面圆的半径为1,三棱锥的底面是底边长2的等腰直角三角形,圆锥的高和棱锥的高相等均为3,故该几何体的体积为 × ×π×12×3+ × × × ×3= +1,故选A.
6.(2016·全国Ⅲ,9)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( )
A.18+36 B.54+18 C.90 D.81
6.B[由题意知,几何体为平行六面体,边长分别为3,3,,几何体的表面积S=3×6×2+3×3×2+3××2=54+18.]
7.(2016·全国Ⅱ,6)如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )
A.20π B.24π C.28π D.32π
7.C [由三视图可知,组合体的底面圆的面积和周长均为4π,圆锥的母线长l==4,所以圆锥的侧面积为S锥侧=×4π×4=8π,圆柱的侧面积S柱侧
=4π×4=16π,所以组合体的表面积S=8π+16π+4π=28π,故选C.]
8.(2016·北京,6)某三棱锥的三视图如图所示,则该三棱锥的体积为( )
A. B. C. D.1
8.A[由三视图知,三棱锥如图所示:由侧视图得高h=1,又底面积S=×1×1=.所以体积V=Sh=.]
9.(2016·山东,5)一个由半球和四棱锥组成的几何体,其三视图如图所示,则该几何体的体积为( )
A.+π B.+π C.+π D.1+π
9.C[由三视图知,半球的半径R=,四棱锥为底面边长为1,高为1的正四棱锥,
∴V=×1×1×1+×π×=+π,故选C.]
10.(2015·广东,8)若空间中n个不同的点两两距离都相等,则正整数n的取值( )
A.大于5 B.等于5 C.至多等于4 D.至多等于3
10.C [当n=3时显然成立,故排除A,B;由正四面体的四个顶点,两两距离相等,得n
=4时成立,故选C.]
11.(2015·北京,5)某三棱锥的三视图如图所示,则该三棱锥的表面积是( )
A.2+ B.4+ C.2+2 D.5
11.C [该三棱锥的直观图如图所示:过D作DE⊥BC,交BC于E,连接AE,则BC=2,EC=1,AD=1,ED=2,
S表=S△BCD+S△ACD+S△ABD+S△ABC
=×2×2+××1+××1+×2×=2+2.]
12.(2015·浙江,2)某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )
A.8 cm3 B.12 cm3 C.cm3 D. cm3
12.C [该几何体是棱长为2 cm的正方体与一底面边长为2 cm的正方形,高为2 cm的正四棱锥组成的组合体,V=2×2×2+×2×2×2=(cm3).故选C.]
13.(2015·新课标全国Ⅰ,11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=( )
A.1 B.2 C.4 D.8
13.B [由题意知,2r·2r+·2πr·2r+πr2+πr2+·4πr2=4r2+5πr2=16+20π,解得r=2.]
14.(2014·福建,2)某空间几何体的正视图是三角形,则该几何体不可能是( )
A.圆柱 B.圆锥 C.四面体 D.三棱柱
14.A [圆柱的正视图是矩形,则该几何体不可能是圆柱.]
15.(2014·江西,5)一几何体的直观图如图,下列给出的四个俯视图中正确的是( )
15.B [由直观图可知,该几何体由一个长方体和一个截角三棱柱组成.从上往下看,外层轮廓线是一个矩形,矩形内部有一条线段连接的两个三角形.]
16.(2014·湖北,5)在如图所示的空间直角坐标系Oxyz中,一个四面体的顶点坐标分别是(0,0,2),(2,2,0),(1,2,1),(2,2,2).给出编号为①、②、③、④的四个图,则该四面体的正视图和俯视图分别为( )
A.①和② B.③和① C.④和③ D.④和②
16.D [在空间直角坐标系O-xyz中作出棱长为2的正方体,在该正方体中作出四面体,如图所示,由图可知,该四面体的正视图为④,俯视图为②.选D.]
17.(2014·新课标全国Ⅰ,12)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
A.6 B.4 C.6 D.4
17.C [如图,设辅助正方体的棱长为4,三视图对应的多面体为三棱锥ABCD,最长的棱为AD==6,选C.]
18.(2015·天津,10)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.
18.π [由三视图可知,该几何体由相同底面的两圆锥和圆柱组成,底面半径为1,圆锥的高为1,圆柱的高为2,所以该几何体的体积V=2×π×12×1+π×12×2=π m3.]
19.(2017•江苏,18)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10 cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(Ⅰ)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(Ⅱ)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
19. (Ⅰ)设玻璃棒在CC1上的点为M,玻璃棒与水面的交点为N,
在平面ACM中,过N作NP∥MC,交AC于点P,
∵ABCD﹣A1B1C1D1为正四棱柱,∴CC1⊥平面ABCD,
又∵AC⊂平面ABCD,∴CC1⊥AC,∴NP⊥AC,
∴NP=12cm,且AM2=AC2+MC2 , 解得MC=30cm,
∵NP∥MC,∴△ANP∽△AMC,
∴ = , ,得AN=16cm.
∴玻璃棒l没入水中部分的长度为16cm.
(Ⅱ)设玻璃棒在GG1上的点为M,玻璃棒与水面的交点为N,
在平面E1EGG1中,过点N作NP⊥EG,交EG于点P,
过点E作EQ⊥E1G1 , 交E1G1于点Q,
∵EFGH﹣E1F1G1H1为正四棱台,∴EE1=GG1 , EG∥E1G1 ,
EG≠E1G1 ,
∴EE1G1G为等腰梯形,画出平面E1EGG1的平面图,
∵E1G1=62cm,EG=14cm,EQ=32cm,NP=12cm,
∴E1Q=24cm,
由勾股定理得:E1E=40cm,
∴sin∠EE1G1= ,sin∠EGM=sin∠EE1G1= ,cos ,
根据正弦定理得: = ,∴sin ,
cos ,∴sin∠GEM=sin(∠EGM+∠EMG)=sin∠EGMcos∠EMG+cos∠EGMsin∠EMG= ,∴EN= = =20cm.∴玻璃棒l没入水中部分的长度为20cm.
考点2 空间几何体的表面积和体积
1.(2018全国Ⅲ,10)设A , B , C , D是同一个半径为4的球的球面上四点,△ABC为等边三角形且其面积为93,则三棱锥D−ABC体积的最大值为( )
A.123 B.183 C.243 D.543
1.B 如图所示,
点M为三角形ABC的重心,E为AC中点,当DM⊥平面ABC时,三棱锥D-ABC体积最大,此时,OD=OB=R=4.∵S△ABC=34AB2=93,∴AB=6,∵点M为三角形ABC的重心,∴BM=23BE=23.∴Rt△ABC中,有OM=OB2-BM2=2,∴DM=OD+OM=4+2=6,∴(VD-ABC)max=13×93×6=183,故选B.
2.(2017•新课标Ⅰ,7)某多面体的三视图如图所示,其中正视图和左视图都由正方形和等腰直角三角形组成,正方形的边长为2,俯视图为等腰直角三角形,该多面体的各个面中有若干个是梯形,这些梯形的面积之和为( )
A.10 B.12 C.14 D.16
2. B 由三视图可画出直观图,该立体图中只有两个相同的梯形的面,S梯形= ×2×(2+4)=6,∴这些梯形的面积之和为6×2=12,故选B.
3.(2017•新课标Ⅱ,4)如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )
A.90π B.63π C.42π D.36π
3. B 由三视图可得,直观图为一个完整的圆柱减去一个高为6的圆柱的一半,
V=π•32×10﹣ •π•32×6=63π,故选B.
4.(2017•新课标Ⅲ,8)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为( )
A.π B. C. D.
4.B ∵圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,∴该圆柱底面圆周半径r= = ,∴该圆柱的体积:V=Sh= = .故选B.
5.(2017•北京,7)某四棱锥的三视图如图所示,则该四棱锥的最长棱的长度为( )
A.3 B.2 C.2 D.2
5.B 由三视图可得直观图,在四棱锥P﹣ABCD中,最长的棱为PA,
即PA= = =2 ,
故选B.
6.(2016·全国Ⅲ,10)在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球,若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是( )
A.4π B. C.6π D.
6.B[由题意知,底面三角形的内切圆直径为4.三棱柱的高为3,所以球的最大直径为3,V的最大值为.]
7.(2016·全国Ⅰ,6)如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是( )
A.17π B.18π C.20π D.28π
7.A[由题知,该几何体的直观图如图所示,它是一个球(被过球心O且互相垂直的三个平面)切掉左上角的后得到的组合体,其表面积是球面面积的和三个圆面积之和,易得球的半径为2,则得S=×4π×22+3×π×22=17π,故选A.]
8.(2015·陕西,5)一个几何体的三视图如图所示,则该几何体的表面积为( )
A.3π B.4π C.2π+4 D.3π+4
8.D [由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为:
S=2×π×12+×2π×1×2+2×2=π+2π+4=3π+4.]
9.(2015·安徽,7)一个四面体的三视图如图所示,则该四面体的表面积是( )
A.1+ B.2+ C.1+2 D.2
9.B [由空间几何体的三视图可得
该空间几何体的直观图,如图,∴该四面体的表面积为S表=2××2×1+2××()2=2+,故选B.]
10.(2015·新课标全国Ⅱ,9)已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,若三棱锥O-ABC体积的最大值为36,则球O的表面积为( )
A.36π B.64π C.144π D.256π
10.C [如图,
要使三棱锥O-ABC即C-OAB的体积最大,当且仅当点C到平面OAB的距离,即三棱锥C-OAB底面OAB上的高最大,其最大值为球O的半径R,则VO-ABC最大=VC-OAB最大=×S△OAB×R=××R2×R=R3=36,所以R=6,得S球O=4πR2=4π×62=144π,选C.]
11.(2015·山东,7)在梯形ABCD中,∠ABC=,AD∥BC,BC=2AD=2AB=2.将梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )
A. B. C. D.2π
11.C [如图,由题意,得BC=2,AD=AB=1.绕AD所在直线旋转一周后所得几何体为一个圆柱挖去一个圆锥的组合体.
所求体积V=π×12×2-π×12×1=π.]
12.(2015·重庆,5)某几何体的三视图如图所示,则该几何体的体积为( )
A.+π B.+π C.+2π D.+2π
12.A [这是一个三棱锥与半个圆柱的组合体,V=π×12×2+××1=π+,选A.]
13.(2015·新课标全国Ⅱ,6)一个正方体被一个平面截去一部分后,剩余部分的三视图如图所示,则截去部分体积与剩余部分体积的比值为( )
A. B. C. D.
13.D [如图,
由题意知,该几何体是正方体ABCD-A1B1C1D1被过三点A、B1、D1的平面所截剩余部分,截去的部分为三棱锥A-A1B1D1,设正方体的棱长为1,则截去部分体积与剩余部分体积的比值为==,选D.]
14.(2015·湖南,10)某工件的三视图如图所示,现将该工件通过切削,加工成一个体积尽可能大的长方体新工件,并使新工件的一个面落在原工件的一个面内,则原工件材料的利用率为(材料利用率=)( )
A. B. C. D.
14.A [易知原工件为一圆锥,V1=πr2h=π,设内接长方体长、宽、高为a、b、c,欲令体积最大,则a=b.由截面图的相似关系知,c+=2,即c+a=2,
∴V长方体=abc=a2c=a2(2-a),
设g(a)=2a2-a3,则g′(a)=4a-3a=0,令g′(a)=0,解得a=,所以令a=时,V长方体
最大为,∴==.故选A.]
15.(2014·重庆,7)某几何体的三视图如图所示,则该几何体的表面积为( )
A.54 B.60 C.66 D.72
15.B [该几何体的直观图如图所示,
易知该几何体的表面是由两个直角三角形,两个直角梯形和一个矩形组成的,则其表面积S=×3×4+×3×5+×5+×4+3×5=60.选B.]
16.(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
A.90 cm2 B.129 cm2 C.132 cm2 D.138 cm2
16.D [由三视图可知该几何体由一个直三棱柱与一个长方体组合而成(如图),
其表面积为S=3×5+2××4×3+4×3+3×3+2×4×3+2×4×6+3×6=138(cm2).]
17.(2014·大纲全国,8)正四棱锥的顶点都在同一球面上.若该棱锥的高为4,底面边长为2,则该球的表面积为( )
A. B.16π C.9π D.
17.A [设球的半径为R,由题意可得(4-R)2+()2=R2,解得R=,所以该球的表面积为4πR2=.故选A.]
18.(2014·安徽,7)一个多面体的三视图如图所示,则该多面体的表面积为( )
A.21+ B.18+ C.21 D.18
18.A [根据题意作出直观图如图,
该多面体是由正方体切去两个角而得到的,根据三视图可知其表面积为6(22-×1×1)+2××()2=6×+=21+.故选A.]
19.(2014·陕西,5)已知底面边长为1,侧棱长为的正四棱柱的各顶点均在同一个球面上,则该球的体积为( )
A. B.4π C.2π D.
19.D [如图为正四棱柱AC1.根据题意得AC=,
∴对角面ACC1A1为正方形,∴外接球直径2R=A1C=2,∴R=1,∴V球=,故选D.]
20.(2014·湖北,8)《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土,这是我国现存最早的有系统的数学典籍,其中记载有求“囷盖”的术:置如其周,令相乘也.又以高乘之,三十六成一.该术相当于给出了由圆锥的底面周长L与高h,计算其体积V的近似公式V≈L2h.它实际上是将圆锥体积公式中的圆周率π近似取为3.那么,近似公式V≈L2h相当于将圆锥体积公式中的π近似取为( )
A. B. C. D.
20.B [圆锥的体积V=πr2h=πh=,由题意得12π≈,π近似取为,故选B.]
21.(2014·新课标全国Ⅱ,6)如图,网格纸上正方形小格的边长为1(表示1 cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3 cm,高为6 cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为( )
A. B. C. D.
21.C [由三视图知该零件是两个圆柱的组合体.一个圆柱的底面半径为2 cm,高为4 cm;另一个圆柱的底面半径为3 cm,高为2 cm.则零件的体积V1=π×22×4+π×32×2=34π(cm3).而毛坯的体积V=π×32×6=54π(cm3),因此切削掉部分的体积V2=V-V1=54π-34π=20π(cm3),所以==.故选C.]
22.(2018全国Ⅱ,16)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为78,SA与圆锥底面所成角为45°,若△SAB的面积为515,则该圆锥的侧面积为__________.
22.402π 因为母线SA,SB所成角的余弦值为78,所以母线SA,SB所成角的正弦值为158,因为△SAB的面积为515,设母线长为l,所以12×l2×158=515∴l2=80,因为SA与圆锥底面所成角为45°,所以底面半径为lcosπ4=22l,因此圆锥的侧面积为πrl=22πl2=402π.
23.(2018天津,11)已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为__________.
23.112 由题意可得,底面四边形EFGH为边长为22的正方形,其面积SEFGH=222=12,
顶点M到底面四边形EFGH的距离为d=12,由四棱锥的体积公式可得:VM−EFGH=13×12×12=112.
24.(2018江苏,10)如图所示,正方体的棱长为2,以其所有面的中心为顶点的多面体的体积为________.
24.43 由图可知,该多面体为两个全等正四棱锥的组合体,正四棱锥的高为1,底面正方形的边长等于2,,所以该多面体的体积为2×13×1×(2)2=43.
25.(2017•新课标Ⅰ,16)如图,圆形纸片的圆心为O,半径为5cm,该纸片上的等边三角形ABC的中心为O.D、E、F为圆O上的点,△DBC,△ECA,△FAB分别是以BC,CA,AB为底边的等腰三角形.沿虚线剪开后,分别以BC,CA,AB为折痕折起△DBC,△ECA,△FAB,使得D、E、F重合,得到三棱锥.当△ABC的边长变化时,所得三棱锥体积(单位:cm3)的最大值为________.
25. 4 cm3 由题意,连接OD,交BC于点G,由题意得OD⊥BC,OG= BC,
即OG的长度与BC的长度成正比,设OG=x,则BC=2 x,DG=5﹣x,
26.(2017•山东,13)由一个长方体和两个 圆柱体构成的几何体的三视图如图,则该几何体的体积为________.
26. 2+ 由长方体长为2,宽为1,高为1,则长方体的体积V1=2×1×1=2,
圆柱的底面半径为1,高为1,则圆柱的体积V2= ×π×12×1= ,
则该几何体的体积V=V1+2V1=2+ ,故答案为:2+ .
27.(2017·天津,10)已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为________.
27. 设正方体的棱长为a, ∵这个正方体的表面积为18, ∴6a2=18,则a2=3,即a= ,∵一个正方体的所有顶点在一个球面上,∴正方体的体对角线等于球的直径,
即 a=2R,即R= ,则球的体积V= π•( )3= ;故答案为: .
28.(2017•江苏,6)如图,在圆柱O1O2内有一个球O,该球与圆柱的上、下底面及母线均相切,记圆柱O1O2的体积为V1 , 球O的体积为V2 , 则 的值是________.
28. 设球的半径为R,则球的体积为: R3 , 圆柱的体积为:πR2•2R=2πR3 .
则 = = .故答案为: .
29.(2016·四川,13)已知三棱锥的四个面都是腰长为2的等腰三角形,该三棱锥的正视图如图所示,则该三棱锥的体积是________.
29. [由题可知,∵三棱锥每个面都是腰为2的等腰三角形,由正视图可得如右俯视图,且三棱锥高为h=1,则面积V=Sh=××1=.]
30.(2016·浙江,14)如图,在△ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是________.
30.[设PD=DA=x,在△ABC中,AB=BC=2,∠ABC=120°,
∴AC===2,
∴CD=2-x,且∠ACB=(180°-120°)=30°,
∴S△BCD=BC·DC×sin∠ACB=×2×(2-x)×=(2-x).
要使四面体体积最大,当且仅当点P到平面BCD的距离最大,而P到平面BCD的最大距离为x.则V四面体PBCD=×(2-x)x=[-(x-)2+3],
由于0<x<2,故当x=时,V四面体PBCD的最大值为×3=.]
31.(2015·江苏,9)现有橡皮泥制作的底面半径为5,高为4的圆锥和底面半径为2、高为8的圆柱各一个.若将它们重新制作成总体积与高均保持不变,但底面半径相同的新的圆锥与圆柱各一个,则新的底面半径为________.
31. [设新的底面半径为r,由题意得πr2·4+πr2·8=π×52×4+π×22×8,解得r=.]
32.(2014·江苏,8)设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2,若它们的侧面积相等,且=,则的值是________.
32. [设圆柱甲的底面半径为r1,高为h1,圆柱乙的底面半径为r2,高为h2.
由题意得==,∴=.又∵S甲侧=S乙侧,即2πr1h1=2πr2h2,
∴==,故==·=×=.]
考点3 点、线、面的位置关系
1.(2018全国Ⅰ,12)已知正方体的棱长为1,每条棱所在直线与平面α所成的角都相等,则α截此正方体所得截面面积的最大值为( )
A.334 B.233 C.324 D.32
1.A 根据相互平行的直线与平面所成的角是相等的,所以在正方体ABCD−A1B1C1D1中,平面AB1D1与线AA1,A1B1,A1D1所成的角是相等的,所以平面AB1D1与正方体的每条棱所在的直线所成角都是相等的,同理平面C1BD也满足与正方体的每条棱所在的直线所成角都是相等,要求截面面积最大,则截面的位置为夹在两个面AB1D1与C1BD中间的,
且过棱的中点的正六边形,且边长为22,所以其面积为S=6×34⋅(22)2=334,故选A.
2.(2017•新课标Ⅱ,10)已知直三棱柱ABC﹣A1B1C1中,∠ABC=120°,AB=2,BC=CC1=1
,则异面直线AB1与BC1所成角的余弦值为( )
A. B. C. D.
2. C 如图所示,设M、N、P分别为AB,BB1和B1C1的中点,则AB1、BC1夹角为MN和NP夹角或其补角(因异面直线所成角为(0, ]),可知MN= AB1= ,NP= BC1= ;
作BC中点Q,则△PQM为直角三角形;∵PQ=1,MQ= AC,△ABC中,由余弦定理得
AC2=AB2+BC2﹣2AB•BC•cos∠ABC=4+1﹣2×2×1×(﹣ )=7,∴AC= ,∴MQ= ;
在△MQP中,MP= = ;在△PMN中,由余弦定理得
cos∠MNP= = =﹣ ;
又异面直线所成角的范围是(0, ],∴AB1与BC1所成角的余弦值为 .
3. (2016·全国Ⅰ,11)平面α过正方体ABCD-A1B1C1D1的顶点A,α∥平面CB1D1,α∩平面ABCD=m,α∩平面ABB1A1=n,则m,n所成角的正弦值为( )
A. B. C. D.
3. A[如图所示,设平面CB1D1∩平面ABCD=m1,∵α∥平面CB1D1,则m1∥m,
又∵平面ABCD∥平面A1B1C1D1,平面CB1D1∩平面A1B1C1D1=B1D1,
∴B1D1∥m1,∴B1D1∥m,同理可得CD1∥n.
故m、n所成角的大小与B1D1、CD1所成角的大小相等,即∠CD1B1的大小.
而B1C=B1D1=CD1(均为面对角线),因此∠CD1B1=,得sin∠CD1B1=,故选A.]
4.(2015·安徽,5)已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是( )
A.若α,β垂直于同一平面,则α与β平行
B.若m,n平行于同一平面,则m与n平行
C.若α,β不平行,则在α内不存在与β平行的直线
D.若m,n不平行,则m与n不可能垂直于同一平面
4.D [对于A,α,β垂直于同一平面,α,β关系不确定,A错;对于B,m,n平行于同一平面,m,n关系不确定,可平行、相交、异面,故B错;对于C,α,β不平行,但α内能找出平行于β的直线,如α中平行于α,β交线的直线平行于β,故C错;对于D,若假设m,n垂直于同一平面,则m∥n,其逆否命题即为D选项,故D正确.]
5.(2014·辽宁,4)已知m,n表示两条不同直线,α表示平面.下列说法正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥α,n⊂α,则m⊥n
C.若m⊥α,m⊥n,则n∥α
D.若m∥α,m⊥n,则n⊥α
5.B [对于选项A,若m∥α,n∥α,则m与n可能相交、平行或异面,A错误;显然选项B正确;对于选项C,若m⊥α,m⊥n,则n⊂α或n∥α,C错误;对于选项D,若m∥α,m⊥n,则n∥α或n⊂α或n与α相交.D错误.故选B.]
6.(2015·浙江,13)如图,三棱锥ABCD中,AB=AC=BD=CD=3,AD=BC=2,点M,N
分别是AD,BC的中点,则异面直线AN,CM所成的角的余弦值是________.
6. [连接DN,作DN的中点O,连接MO,OC.在△AND中.M为AD的中点,则OM綉AN.所以异面直线AN,CM所成角为∠CMO,在△ABC中,AB=AC=3,BC=2,则AN=2,∴OM=.在△ACD中,同理可知CM=2,在△BCD中,DN=2,在Rt△ONC中,ON=,CN=1∴OC=.在△CMO中,由余弦定理cos∠CMO===.]
考点4 线面平行的判定与性质
1.(2017•新课标Ⅱ,19)如图,四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,∠BAD=∠ABC=90°,E是PD的中点.
(Ⅰ)证明:直线CE∥平面PAB;
(Ⅱ)点M在棱PC 上,且直线BM与底面ABCD所成角为45°,求二面角M﹣AB﹣D的余弦值.
1.(Ⅰ)证明:取PA的中点F,连接EF,BF,因为E是PD的中点,所以EF AD,AB=BC= AD,∠BAD=∠ABC=90°,∴BC∥ AD,∴BCEF是平行四边形,可得CE∥BF,BF⊂平面PAB,CF⊄平面PAB,∴直线CE∥平面PAB;
(Ⅱ)解:四棱锥P﹣ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,AB=BC= AD,
∠BAD=∠ABC=90°,E是PD的中点.取AD的中点O,M在底面ABCD上的射影N在OC
上,设AD=2,则AB=BC=1,OP= ,∴∠PCO=60°,直线BM与底面ABCD所成角为45°,可得:BN=MN,CN= MN,BC=1,可得:1+ BN2=BN2 , BN= ,MN= ,作NQ⊥AB于Q,连接MQ,所以∠MQN就是二面角M﹣AB﹣D的平面角,MQ= = ,二面角M﹣AB﹣D的余弦值为: = .
2.(2017•江苏,15)如图,在三棱锥A﹣BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E、F(E与A、D不重合)分别在棱AD,BD上,且EF⊥AD.
求证:(Ⅰ)EF∥平面ABC;
(Ⅱ)AD⊥AC.
2.证明:(Ⅰ)因为AB⊥AD,EF⊥AD,且A、B、E、F四点共面, 所以AB∥EF,
又因为EF⊊平面ABC,AB⊆平面ABC,
所以由线面平行判定定理可知:EF∥平面ABC;
(Ⅱ)在线段CD上取点G,连结FG、EG使得FG∥BC,则EG∥AC,
因为BC⊥BD,所以FG⊥BC,
又因为平面ABD⊥平面BCD,
所以FG⊥平面ABD,所以FG⊥AD,
又因为AD⊥EF,且EF∩FG=F,
所以AD⊥平面EFG,所以AD⊥EG,
故AD⊥AC.
3.(2016·山东,17)在如图所示的圆台中,AC是下底面圆O的直径,EF是上底面圆O′的直径,FB是圆台的一条母线.
(1)已知G,H分别为EC,FB的中点,求证:GH∥平面ABC;
(2)已知EF=FB=AC=2,AB=BC,求二面角F-BC-A的余弦值.
3.(1)证明设FC中点为I,连接GI,HI,在△CEF中,因为点G是CE的中点,所以GI∥EF.
又EF∥OB,所以GI∥OB.在△CFB中,因为H是FB的中点,所以HI∥BC,
又HI∩GI=I,所以平面GHI∥平面ABC.
因为GH⊂平面GHI,所以GH∥平面ABC.
(2)连接OO′,则OO′⊥平面ABC.又AB=BC,且AC是圆O的直径,所以BO⊥AC.
以O为坐标原点,建立如图所示的空间直角坐标系O-xyz.
由题意得B(0,2,0),C(-2,0,0).过点F作FM垂直OB于点M,
所以FM==3,可得F(0,,3).故=(-2,-2,0),=(0,-,3).
设m=(x,y,z)是平面BCF的一个法向量.由可得
可得平面BCF的一个法向量m=,
因为平面ABC的一个法向量n=(0,0,1),所以cos〈m,n〉==.
所以二面角F-BC-A的余弦值为.
4.(2016·全国Ⅲ,19)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.
(1)证明MN∥平面PAB;
(2)求直线AN与平面PMN所成角的正弦值.
4.(1)证明 由已知得AM=AD=2.
取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.
又AD∥BC,故TN綉AM,四边形AMNT为平行四边形,于是MN∥AT.
因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.
(2)解 取BC的中点E,连接AE.由AB=AC得AE⊥BC,
从而AE⊥AD,AE===.
以A为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系A-xyz.
由题意知,P(0,0,4),M(0,2,0),C(,2,0),N,=(0,2,-4),=,=.
设n=(x,y,z)为平面PMN的法向量,则即
可取n=(0,2,1).于是cos〈n,〉==.
设AN与平面PMN所成的角为θ,则sin θ=,
∴直线AN与平面PMN所成的角的正弦值为.
5.(2015·江苏,16)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1.设AB1的中点为D,B1C∩BC1=E.
求证:(1)DE∥平面AA1C1C;
(2)BC1⊥AB1.
5.证明 (1)由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.
又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.
(2)因为棱柱ABCA1B1C1是直三棱柱,所以CC1⊥平面ABC.
因为AC⊂平面ABC,所以AC⊥CC1.
又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.
又因为BC1⊂平面BCC1B1,所以BC1⊥AC.
因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.
因为AC,B1C⊂平面B1AC,AC∩B1C=C,,所以BC1⊥平面B1AC.
又因为AB1⊂平面B1AC,所以BC1⊥AB1.
6.(2014·江苏,16)如图,在三棱锥PABC中,D,E,F分别为棱PC,AC,AB的中点.已知PA⊥AC,PA=6,BC=8,DF=5.
求证:(1)直线PA∥平面DEF;
(2)平面BDE⊥平面ABC.
6.证明 (1)因为D,E分别为棱PC,AC的中点,所以DE∥PA.
又因为PA⊄平面DEF,DE⊂平面DEF,所以直线PA∥平面DEF.
(2)因为D,E,F分别为棱PC,AC,AB的中点,PA=6,BC=8,所以DE∥PA,DE=PA=3,
EF=BC=4.又因为DF=5,故DF2=DE2+EF2,所以∠DEF=90°,即DE⊥EF.
又PA⊥AC,DE∥PA,所以DE⊥AC.
因为AC∩EF=E,AC⊂平面ABC,EF⊂平面ABC,所以DE⊥平面ABC.
又DE⊂平面BDE,所以平面BDE⊥平面ABC.
7.(2014·新课标全国Ⅱ,18)如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.
(1)证明:PB∥平面AEC;
(2)设二面角DAEC为60°,AP=1,AD=,
求三棱锥EACD的体积.
7.(1)证明 连接BD交AC于点O,连接EO.因为ABCD为矩形,所以O为BD的中点.
又E为PD的中点,所以EO∥PB.又因为EO⊂平面AEC,PB⊄平面AEC,所以PB∥平面AEC.
(2) 因为PA⊥平面ABCD,ABCD为矩形,所以AB,AD,AP两两垂直.
如图,以A为坐标原点,的方向为x轴的正方向,||为单位长,建立空间直角坐标系Axyz,则D(0,,0),E,=.
设B(m,0,0)(m>0),则C(m,,0),=(m,,0).
设n1=(x,y,z)为平面ACE的法向量,则即
可取n1=.
又n2=(1,0,0)为平面DAE的法向量,由题设知|cos〈n1,n2〉|=,即=,解得m=.因为E为PD的中点,所以三棱锥EACD的高为,三棱锥EACD的体积V=××××=.
8.(2014·湖北,19)如图,在棱长为2的正方体ABCDA1B1C1D1中,E,F,M,N分别是棱AB,AD,A1B1,A1D1的中点,点P,Q分别在棱DD1,BB1上移动,且DP=BQ=λ(0<λ<2).
(1)当λ=1时,证明:直线BC1∥平面EFPQ;
(2)是否存在λ,使面EFPQ与面PQMN所成的二面角为直二面角?若存在,求出λ的值;若不存在,说明理由.
8.法一(几何法)
(1)证明 如图1,连接AD1,由ABCDA1B1C1D1是正方体,知BC1∥AD1.
当λ=1时,P是DD1的中点,又F是AD的中点,所以FP∥AD1.所以BC1∥FP.
而FP⊂平面EFPQ,且BC1⊄平面EFPQ,故直线BC1∥平面EFPQ.
(2) 如图2,连接BD.因为E,F分别是AB,AD的中点,所以EF∥BD,且EF=BD.
又DP=BQ,DP∥BQ,所以四边形PQBD是平行四边形,故PQ∥BD,且PQ=BD,
从而EF∥PQ,且EF=PQ.
在Rt△EBQ和Rt△FDP中,因为BQ=DP=λ,BE=DF=1,
于是EQ=FP=,所以四边形EFPQ是等腰梯形.
同理可证四边形PQMN是等腰梯形.
分别取EF,PQ,MN的中点为H,O,G,连接OH,OG,
则GO⊥PQ,HO⊥PQ,而GO∩HO=O,
故∠GOH是面EFPQ与面PQMN所成的二面角的平面角.
若存在λ,使面EFPQ与面PQMN所成的二面角为直二面角,则∠GOH=90°.
连接EM,FN,则由EF∥MN,且EF=MN,知四边形EFNM是平行四边形.
连接GH,因为H,G是EF,MN的中点,所以GH=ME=2.
在△GOH中,GH2=4,OH2=1+λ2-=λ2+,
OG2=1+(2-λ)2-=(2-λ)2+,
由OG2+OH2=GH2,得(2-λ)2++λ2+=4,解得λ=1±,
故存在λ=1±,使面EFPQ与面PQMN所成的二面角为直二面角.
法二(向量方法)
以D为原点,射线DA,DC,DD1分别为x,y,z轴的正半轴建立如图3所示的空间直角坐标系Dxyz.由已知得B(2,2,0),C1(0,2,2),E(2,1,0),F(1,0,0),P(0,0,λ).
=(-2,0,2),=(-1,0,λ),=(1,1,0).
(1)证明 当λ=1时,=(-1,0,1),
又因为=(-2,0,2),所以=2,即BC1∥FP.
而FP⊂平面EFPQ,且BC1⊄平面EFPQ,故直线BC1∥平面EFPQ.
(2)解 设平面EFPQ的一个法向量为n=(x,y,z),
则由可得于是可取n=(λ,-λ,1).
同理可得平面MNPQ的一个法向量为m=(λ-2,2-λ,1).
若存在λ,使面EFPQ与面PQMN所成的二面角为直二面角,
则m·n=(λ-2,2-λ,1)·(λ,-λ,1)=0,即λ(λ-2)-λ(2-λ)+1=0,解得λ=1±.
故存在λ=1±,使面EFPQ与面PQMN所成的二面角为直二面角.
考点5 线面垂直的判定与性质
1.(2016·浙江,2)已知互相垂直的平面α,β交于直线l.若直线m,n满足m∥α,n⊥β,则( )
A.m∥l B.m∥n C.n⊥l D.m⊥n
1.C [由已知,α∩β=l,∴l⊂β,又∵n⊥β,∴n⊥l,C正确.故选C.]
2.(2015·浙江,8)如图,已知△ABC,D是AB的中点,沿直线CD将△ACD翻折成△A′CD,所成二面角A′CDB的平面角为α,则( )
A.∠A′DB≤α B.∠A′DB≥α
C.∠A′CB≤α D.∠A′CB≥α
2.B [极限思想:若α=π,则∠A′CB<π,排除D;若α=0,如图,则∠A′DB,∠A′CB都可以大于0,排除A,C.故选B. ]
3.(2014·广东,7)若空间中四条两两不同的直线l1,l2,l3,l4,满足l1⊥l2,l2⊥l3,l3⊥l4,则下列结论一定正确的是( )
A.l1⊥l4 B.l1∥l4 C.l1与l4既不垂直也不平行 D.l1与l4的位置关系不确定
3.D [构造如图所示的正方体ABCDA1B1C1D1,取l1为AD,l2为AA1,l3为A1B1,
当取l4为B1C1时,l1∥l4,当取l4为BB1时,l1⊥l4,故排除A、B、C,选D.]
4.(2016·全国Ⅱ,14)α,β是两个平面,m,n是两条直线,有下列四个命题:
(1)如果m⊥n,m⊥α,n∥β,那么α⊥β.
(2)如果m⊥α,n∥α,那么m⊥n.
(3)如果α∥β,m⊂α,那么m∥β.
(4)如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.
其中正确的命题有________(填写所有正确命题的编号).
4.②③④ [当m⊥n,m⊥α,n∥β时,两个平面的位置关系不确定,故①错误,经判断知②③④均正确,故正确答案为②③④.]
5.(2018江苏,15)在平行六面体ABCD−A1B1C1D1中,AA1=AB,AB1⊥B1C1。
求证:(1)AB//平面A1B1C;
(2)平面ABB1A1⊥平面A1BC.
5.证明:(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.
因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,
所以AB∥平面A1B1C.
(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.
又因为AA1=AB,所以四边形ABB1A1为菱形,
因此AB1⊥A1B.
又因为AB1⊥B1C1,BC∥B1C1,
所以AB1⊥BC.
又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,
所以AB1⊥平面A1BC.
因为AB1⊂平面ABB1A1,
所以平面ABB1A1⊥平面A1BC.
6.(2017•新课标Ⅰ,18)如图,在四棱锥P﹣ABCD中,AB∥CD,且∠BAP=∠CDP=90°
(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,∠APD=90°,求二面角A﹣PB﹣C的余弦值.
6.(1)证明:∵∠BAP=∠CDP=90°,∴PA⊥AB,PD⊥CD, ∵AB∥CD,∴AB⊥PD,
又∵PA∩PD=P,且PA⊂平面PAD,PD⊂平面PAD,
∴AB⊥平面PAD,又AB⊂平面PAB,
∴平面PAB⊥平面PAD;
(2)解:∵AB∥CD,AB=CD,∴四边形ABCD为平行四边形, 由(1)知AB⊥平面PAD,∴AB⊥AD,则四边形ABCD为矩形,
在△APD中,由PA=PD,∠APD=90°,可得△PAD为等腰直角三角形,
设PA=AB=2a,则AD= .
取AD中点O,BC中点E,连接PO、OE,
以O为坐标原点,分别以OA、OE、OP所在直线为x、y、z轴建立空间直角坐标系,
则:D( ),B( ),P(0,0, ),C( ).
, , .
设平面PBC的一个法向量为 ,
由 ,得 ,取y=1,得 .
∵AB⊥平面PAD,AD⊂平面PAD,∴AB⊥AD,
又PD⊥PA,PA∩AB=A,
∴PD⊥平面PAB,则 为平面PAB的一个法向量, .
∴cos< >= = .
由图可知,二面角A﹣PB﹣C为钝角,
∴二面角A﹣PB﹣C的余弦值为 .
7.(2017•新课标Ⅲ,19)如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD.
(Ⅰ)证明:平面ACD⊥平面ABC;
(Ⅱ)过AC的平面交BD于点E,若平面AEC把四面体ABCD
分成体积相等的两部分,求二面角D﹣AE﹣C的余弦值.
7.(Ⅰ)证明:如图所示,取AC的中点O,连接BO,OD.∵△ABC是等边三角形,∴OB⊥AC.△ABD与△CBD中,AB=BD=BC,∠ABD=∠CBD,∴△ABD≌△CBD,∴AD=CD.∵△ACD是直角三角形,∴AC是斜边,∴∠ADC=90°.∴DO= AC.∴DO2+BO2=AB2=BD2 . ∴∠BOD=90°.
∴OB⊥OD.又DO∩AC=O,∴OB⊥平面ACD.又OB⊂平面ABC,∴平面ACD⊥平面ABC.
(Ⅱ)设点D,B到平面ACE的距离分别为hD , hE . 则 = .
∵平面AEC把四面体ABCD分成体积相等的两部分,
∴ = = =1.
∴点E是BD的中点.
建立如图所示的空间直角坐标系.不妨设AB=2.
则O(0,0,0),A(1,0,0),C(﹣1,0,0),D(0,0,1),B(0, ,0),E .
=(﹣1,0,1), = , =(﹣2,0,0).
设平面ADE的法向量为 =(x,y,z),则 ,即 ,取
= .
同理可得:平面ACE的法向量为 =(0,1, ).
∴cos = = =﹣ .
∴二面角D﹣AE﹣C的余弦值为 .
8.(2016·全国Ⅰ,18)如图,在以A,B,C,D,E,F为顶点的五面体中,平面ABEF为正方形,AF=2FD,∠AFD=90°,且二面角D-AF-E与二面角C-BE-F都是60°.
(1)证明:平面ABEF⊥EFDC;
(2)求二面角E-BC-A的余弦值.
8.(1)证明 由已知可得AF⊥DF,AF⊥FE,所以AF⊥平面EFDC,又AF⊂平面ABEF,故平面ABEF⊥平面EFDC.
(2)解过D作DG⊥EF,垂足为G,由(1)知DG⊥平面ABEF.以G为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系G-xyz.
由(1)知∠DFE为二面角D-AF-E的平面角,故∠DFE=60°,则|DF|=2,|DG|=,可得A(1,4,0),B(-3,4,0),E(-3,0,0),D(0,0,).
由已知,AB∥EF,所以AB∥平面EFDC,又平面ABCD∩平面EFDC=CD,故AB∥CD,CD∥EF,
由BE∥AF,可得BE⊥平面EFDC,所以∠CEF为二面角C-BE-F的平面角,∠CEF=60°,从而可得C(-2,0,).所以=(1,0,),=(0,4,0),=(-3,-4,),=(-4,0,0).
设n=(x,y,z)是平面BCE的法向量,则即所以可取n=(3,0,-).
设m是平面ABCD的法向量,则
同理可取m=(0,,4),则cos〈n,m〉==-.
故二面角E-BC-A的余弦值为-.
9.(2016·江苏,16)如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.
求证:(1)直线DE∥平面A1C1F;
(2)平面B1DE⊥平面A1C1F.
9.证明 (1)由已知,DE为△ABC的中位线,
∴DE∥AC,又由三棱柱的性质可得AC∥A1C1,∴DE∥A1C1,
且DE⊄平面A1C1F,A1C1⊂平面A1C1F,∴DE∥平面A1C1F.
(2)在直三棱柱ABC-A1B1C1中,AA1⊥平面A1B1C1,
∴AA1⊥A1C1,又∵A1B1⊥A1C1,且A1B1∩AA1=A,∴A1C1⊥平面ABB1A1,
∵B1D⊂平面ABB1A1,∴A1C1⊥B1D,
又∵A1F⊥B1D,且A1F∩A1C1=A1,∴B1D⊥平面A1C1F,
又∵B1D⊂平面B1DE,∴平面B1DE⊥平面A1C1F.
10.(2015·新课标全国Ⅱ,19)如图,长方体ABCD-A1B1C1D1中,AB=16,BC=10,AA1=8,点E,F分别在A1B1,D1C1上,A1E=D1F=4.过点E,F的平面α与此长方体的面相交,交线围成一个正方形.
(1)在图中画出这个正方形(不必说明画法和理由);
(2)求直线AF与平面α所成角的正弦值.
10.解 (1)交线围成的正方形EHGF如图:
(2)作EM⊥AB,垂足为M,则AM=A1E=4,EM=AA1=8.
因为EHGF为正方形,所以EH=EF=BC=10.于是MH==6,所以AH=10.
以D为坐标原点,的方向为x轴正方向,建立如图所示的空间直角坐标系Dxyz,则A(10,0,0),H(10,10,0),E(10,4,8),F(0,4,8),=(10,0,0),=(0,-6,8).
设n=(x,y,z)是平面EHGF的法向量,则即所以可取n=(0,4,3).又=(-10,4,8),故|cos〈n,〉|==.
所以AF与平面EHGF所成角的正弦值为.
11.(2015·新课标全国Ⅰ,18)如图,四边形ABCD为菱形,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF,AE⊥EC.
(1)证明:平面AEC⊥平面AFC,
(2)求直线AE与直线CF所成角的余弦值.
11.(1)证明 连接BD,设BD∩AC=G,连接EG,FG,EF.
在菱形ABCD中,不妨设GB=1.由∠ABC=120°,可得AG=GC=.
由BE⊥平面ABCD,AB=BC,可知AE=EC.又AE⊥EC,所以EG=,且EG⊥AC.
在Rt △EBG中,可得BE=,故DF=.
在Rt △FDG中,可得FG=.
在直角梯形BDFE中,由BD=2,BE=,DF=,可得EF=,
从而EG2+FG2=EF2,所以EG⊥FG.
又AC∩FG=G,可得EG⊥平面AFC.
因为EG⊂平面AEC,所以平面AEC⊥平面AFC.
(2)解 如图,以G为坐标原点,分别以,的方向为x轴,y轴正方向,||为单位长,建立空间直角坐标系Gxyz,由(1)可得A(0,-,0),E(1,0,),F,C(0,,0),所以=(1,,),=.故cos〈,〉==-.
所以直线AE与直线CF所成角的余弦值为.
12.(2014·新课标全国Ⅰ,19)如图,三棱柱ABCA1B1C1中,侧面BB1C1C为菱形,AB⊥B1C.
(1)证明:AC=AB1;
(2)若AC⊥AB1,∠CBB1=60°,AB=BC,求二面角AA1B1C1的余弦值.
12.(1)证明 连接BC1,交B1C于点O,连接AO.
因为侧面BB1C1C为菱形,所以B1C⊥BC1,且O为B1C及BC1的中点.
又AB⊥B1C,所以B1C⊥平面ABO.由于AO⊂平面ABO,故B1C⊥AO.
又B1O=CO,故AC=AB1.
(2)解 因为AC⊥AB1,且O为B1C的中点,所以AO=CO.
又因为AB=BC,所以△BOA≌△BOC.
故OA⊥OB,从而OA,OB,OB1两两互相垂直.
以O为坐标原点,的方向为x轴正方向,||为单位长,建立如图所示的空间直角坐标系Oxyz.
因为∠CBB1=60°,所以△CBB1为等边三角形.又AB=BC,则A, B(1,0,0),B1,C.
=,==,==.
设n=(x,y,z)是平面AA1B1的法向量,则即
所以可取n=(1,,).设m是平面A1B1C1的法向量,则
同理可取m=(1,-,).则cos〈n,m〉==.
所以二面角AA1B1C1的余弦值为.
13.(2014·广东,18)如图,四边形ABCD为正方形,PD⊥平面ABCD,∠DPC=30°,AF⊥PC于点F,FE∥CD,交PD于点E.
(1)证明:CF⊥平面ADF;
(2)求二面角DAFE的余弦值.
13.(1)证明 ∵PD⊥平面ABCD,∴PD⊥AD.又CD⊥AD,PD∩CD=D,
∴AD⊥平面PCD.∴AD⊥PC.
又AF⊥PC,AD∩AF=A,∴PC⊥平面ADF,即CF⊥平面ADF.
(2)解 法一 设AB=1,则在Rt△PDC中,CD=1,∵∠DPC=30°,
∴PC=2,PD=,由(1)知CF⊥DF,∴DF=,CF=.
又FE∥CD,∴==,∴DE=.同理EF=CD=.
如图所示,以D为原点,建立空间直角坐标系,则A(0,0,1),
E,F,P(,0,0),C(0,1,0).
设m=(x,y,z)是平面AEF的法向量,则又
∴令x=4,则z=,m=(4,0,).
由(1)知平面ADF的一个法向量为=(-,1,0),
设二面角DAFE的平面角为θ,可知θ为锐角,
cos θ=|cos〈m,〉|===.
故二面角DAFE的余弦值为.
法二 设AB=1,
∵CF⊥平面ADF,∴CF⊥DF.∴在△CFD中,DF=,
∵CD⊥AD,CD⊥PD,∴CD⊥平面ADE.又∵EF∥CD,∴EF⊥平面ADE.∴EF⊥AE,
∴在△DEF中,DE=,EF=,
在△ADE中,AE=,在△ADF中,AF=.
由VADEF=·S△ADE·EF=·S△ADF·hEADF,解得hEADF=,
设△AEF的边AF上的高为h,
由S△AEF=·EF·AE=·AF·h,解得h=×,
设二面角DAFE的平面角为θ.
则sin θ==××=,∴cos θ=.
14.(2014·辽宁,19)如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角EBFC的正弦值.
14.(1)证明 法一 过E作EO⊥BC,垂足为O,连接OF.
图1
由△ABC≌△DBC可证出△EOC≌△FOC.所以∠EOC=∠FOC=,即FO⊥BC.
又EO⊥BC,因此BC⊥面EFO,又EF⊂面EFO,所以EF⊥BC.
法二 由题意,以B为坐标原点,在平面DBC内过B作垂直BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示空间直角坐标系.易得B(0,0,0),A(0,-1,),D(,-1,0),C(0,2,0).
因而E(0,,),F,所以=,=(0,2,0),因此·=0.
从而⊥,所以EF⊥BC.
图2
(2)解 法一 在图1中,过O作OG⊥BF,垂足为G,连接EG.
由平面ABC⊥平面BDC,从而EO⊥面BDC,又OG⊥BF,由三垂线定理知,EG⊥BF.
因此∠EGO为二面角EBFC的平面角.
在△EOC中,EO=EC=BC·cos 30°=,由△BGO∽△BFC知,OG=·FC=,因此tan∠EGO==2,从而sin∠EGO=,即二面角EBFC的正弦值为.
法二 在图2中,平面BFC的一个法向量为n1=(0,0,1).
设平面BEF的法向量n2=(x,y,z),
又=,=.由得其中一个n2=(1,-,1).
设二面角EBFC大小为θ,且由题意知θ为锐角,则
cos θ=|cos〈n1,n2〉|==,
因此sin θ==,即所求二面角的正弦值为.
15.(2014·江西,19)如图,四棱锥PABCD中,ABCD为矩形,平面PAD⊥平面ABCD.
(1)求证:AB⊥PD;
(2)若∠BPC=90°,PB=,PC=2,问AB为何值时,四棱锥PABCD的体积最大?并求此时平面BPC与平面DPC夹角的余弦值.
15.(1)证明 ABCD为矩形,故AB⊥AD;又平面PAD⊥平面ABCD,
平面PAD∩平面ABCD=AD,
所以AB⊥平面PAD,由PD⊂平面PAD,故AB⊥PD.
(2)解 过P作AD的垂线,垂足为O,过O作BC的垂线,垂足为G,连接PG.
故PO⊥平面ABCD,BC⊥平面POG,BC⊥PG.
在Rt△BPC中,PG=,GC=,BG=.
设AB=m,则OP==,
故四棱锥PABCD的体积为V=··m·=.
因为m==,
故当m=,即AB=时,四棱锥PABCD的体积最大.
此时,建立如图所示的坐标系,
各点的坐标为O(0,0,0),B,
C,D,P.故=,
=(0,,0),=,
设平面BPC的一个法向量n1=(x,y,1),则由n1⊥,
n1⊥得解得x=1,y=0,n1=(1,0,1).
同理可求出平面DPC的一个法向量n2=.从而平面BPC与平面DPC夹角θ的余弦值为cos θ===.
16.(2014·湖南,19)如图,四棱柱ABCD-A1B1C1D1的所有棱长都相等,AC∩BD=O,A1C1∩B1D1=O1,四边形ACC1A1和四边形BDD1B1均为矩形.
(1)证明:O1O⊥底面ABCD;
(2)若∠CBA=60°,求二面角C1OB1D的余弦值.
16.(1)证明因为四边形ACC1A1为矩形,所以CC1⊥AC,同理DD1⊥BD,因为CC1∥DD1,所以CC1⊥BD,而AC∩BD=O,因此CC1⊥底面ABCD.
由题设知,O1O∥C1C,故O1O⊥底面ABCD.
(2)解 法一 如图,过O1作O1H⊥OB1于H,连接HC1.
由(1)知,O1O⊥底面ABCD,所以O1O⊥底面A1B1C1D1,于是O1O⊥A1C1.
又因为四棱柱ABCDA1B1C1D1的所有棱长都相等,所以四边形A1B1C1D1是菱形,
因此A1C1⊥B1D1,从而A1C1⊥平面BDD1B1,所以A1C1⊥OB1,于是OB1⊥平面O1HC1,
进而OB1⊥C1H,故∠C1HO1是二面角C1OB1D的平面角.
不妨设AB=2.因为∠CBA=60°,所以OB=,OC=1,OB1=.
在Rt△OO1B1中,易知O1H==2,而O1C1=1,
于是C1H===.
故cos∠C1HO1===.即二面角C1OB1D的余弦值为.
法二 因为四棱柱ABCDA1B1C1D1的所有棱长都相等,所以四边形ABCD是菱形,因此AC⊥BD.又由(1)知O1O⊥底面ABCD,从而OB,OC,OO1两两垂直.
如图,以O为坐标原点,OB,OC,OO1所在直线分别为x轴、y轴、z轴,建立空间直角坐标系Oxyz.不妨设AB=2,因为∠CBA=60°,所以OB=,OC=1.
于是相关各点的坐标为:O(0,0,0),B1(,0,2),C1(0,1,2).
易知,n1=(0,1,0)是平面BDD1B1的一个法向量.
设n2=(x,y,z)是平面OB1C1的法向量,则即
取z=-,则x=2,y=2,所以n2=(2,2,-),
设二面角C1OB1D的大小为θ,易知θ是锐角,于是
cos θ=|cos〈n1,n2〉|=||==.
故二面角C1OB1D的余弦值为.
考点6 空间向量与立体几何
1.(2018全国Ⅱ,9)在长方体ABCD−A1B1C1D1中,AB=BC=1,AA1=3,则异面直线AD1与DB1所成角的余弦值为( )
A.15 B.56 C.55 D.22
1.C 以D为坐标原点,DA,DC,DD1为x,y,z轴建立空间直角坐标系,则D(0,0,0),A(1,0,0),B1(1,1,3),D1(0,0,3),所以AD1=(−1,0,3),DB1=(1,1,3),因为cos=AD1⋅DB1|AD1||DB1|=−1+32×5=55,所以异面直线AD1与DB1所成角的余弦值为55,选C.
2.(2018浙江,8)已知四棱锥S−ABCD的底面是正方形,侧棱长均相等,E是线段AB上的点(不含端点),设SE与BC所成的角为θ1,SE与平面ABCD所成的角为θ2,二面角S−AB−C的平面角为θ3,则( )
A.θ1≤θ2≤θ3 B.θ3≤θ2≤θ1 C.θ1≤θ3≤θ2 D.θ2≤θ3≤θ1
2.D 设O为正方形ABCD的中心,M为AB中点,过E作BC的平行线EF,交CD于F,过O作ON垂直EF于N,连接SO,SN,OM,则SO垂直于底面ABCD,OM垂直于AB,因此∠SEN=θ1,∠SEO=θ2,∠SMO=θ3,从而tanθ1=SNEN=SNOM,tanθ2=SOEO,tanθ3=SOOM,因为SN≥SO,EO≥OM,所以tanθ1≥tanθ3≥tanθ2,即θ1≥θ3≥θ2,选D.
3.(2017•浙江,9)如图,已知正四面体D﹣ABC(所有棱长均相等的三棱锥),P、Q、R分别为AB、BC、CA上的点,AP=PB, = =2,分别记二面角D﹣PR﹣Q,D﹣PQ﹣R,
D﹣QR﹣P的平面角为α、β、γ,则( )
A.γ<α<β B.α<γ<β C.α<β<γ D.β<γ<α
3. B 如图所示,建立空间直角坐标系.设底面△ABC的中心为O.不妨设OP=3.则O(0,0,0),P(0,﹣3,0),C(0,﹣6,0),D(0,0,6 ),Q ,R ,
= , =(0,3,6 ), =( ,5,0), = ,
= .
设平面PDR的法向量为 =(x,y,z),则 ,可得 ,
可得 = ,取平面ABC的法向量 =(0,0,1).则cos = = ,取α=arccos .同理可得:β=arccos .γ=arccos .
∵ > > .∴α<γ<β.
解法二:如图所示,连接OD,OQ,OR,过点O发布作垂线:OE⊥DR,OF⊥DQ,OG⊥QR,垂足分别为E,F,G,连接PE,PF,PG.
设OP=h.
则cosα= = = .
同理可得:cosβ= = ,cosγ= = .
由已知可得:OE>OG>OF.
∴cosα>cosγ>cosβ,α,β,γ为锐角.
∴α<γ<β.
故选B.
4.(2014·广东,5)已知向量a=(1,0,-1),则下列向量中与a成60°夹角的是( )
A.(-1,1,0) B.(1,-1,0) C.(0,-1,1) D.(-1,0,1)
4.B [设选项中的向量与a的夹角为θ,对于选项A,由于cos θ=
=-,此时夹角θ为120°,不满足题意;对于选项B,由于cos θ==,此时夹角θ为60°,满足题意.故选B.]
5.(2014·四川,8)如图,在正方体ABCD-A1B1C1D1中,点O为线段BD的中点.设点P在线段CC1上,直线OP与平面A1BD所成的角为α,则sin α的取值范围是( )
A. B. C. D.
5.B [易证AC1⊥平面A1BD,当点P在线段CC1上从C运动到C1时,直线OP与平面A1BD所成的角α的变化情况:∠AOA1→→∠C1OA1(点P为线段CC1的中点时,α=),由于sin∠AOA1=,sin∠C1OA1=>,sin =1,所以sin α的取值范围是[,1].]
6.(2014·新课标全国Ⅱ,11)直三棱柱ABCA1B1C1中,∠BCA=90°,M,N分别是A1B1,A1C1的中点,BC=CA=CC1,则BM与AN所成角的余弦值为( )
A. B. C. D.
6.C[以C1为坐标原点,建立如图所示的空间直角坐标系,
设BC=CA=CC1=2,则A(2,0,2),N(1,0,0),M(1,1,0),B(0,2,2),∴=(-1,0,-2),=(1,-1,-2),
∴cos〈,〉====,故选C.]
7.(2014·江西,10)如图,在长方体ABCD-A1B1C1D1中,AB=11,AD=7,AA1=12.一质点从顶点A射向点E(4,3,12),遇长方体的面反射(反射服从光的反射原理),将第i-1次到第i次反射点之间的线段记为Li(i=2,3,4),L1=AE,将线段L1,L2,L3,L4
竖直放置在同一水平线上,则大致的图形是( )
7.C [根据反射的对称性,质点是在过A,E,A1的平面内运动.因为<,所以过A、E,A1作长方体的截面AA1NM如图所示.
设点A关于平面A1B1C1D1的对称点为A′,易知它在z轴上,且A′A1=AA1=12,连接A′E并延长交平面ABCD于点E1,因为A1E=5,所以AE1=10,且E1到AB,AD的距离分别为6,8,即E1(8,6,0),而它在线段AM上,从而知L1=AE=EE1=L2;事实上,只需要在AA1NM内,过E1作AE的平行线交MN于点E2,再过E2作E1E的平行线交A1N于点E3,可知EE1>E2E3=L4>E1E2=L3,故L1=L2>L4>L3,故选C.]
8.(2017•新课标Ⅲ,16)a,b为空间中两条互相垂直的直线,等腰直角三角形ABC的直角边AC所在直线与a,b都垂直,斜边AB以直线AC为旋转轴旋转,有下列结论:
①当直线AB与a成60°角时,AB与b成30°角;
②当直线AB与a成60°角时,AB与b成60°角;
③直线AB与a所成角的最小值为45°;
④直线AB与a所成角的最小值为60°;
其中正确的是________(填写所有正确结论的编号)
8. ②③ 由题意知,a、b、AC三条直线两两相互垂直,画出图形如图,不妨设图中所示正方体边长为1,故|AC|=1,|AB|= ,斜边AB以直线AC为旋转轴,则A点保持不变,
B点的运动轨迹是以C为圆心,1为半径的圆,以C坐标原点,以CD为x轴,CB为y轴,CA为z轴,建立空间直角坐标系,
则D(1,0,0),A(0,0,1),直线a的方向单位向量 =(0,1,0),| |=1,
直线b的方向单位向量 =(1,0,0),| |=1,
设B点在运动过程中的坐标中的坐标B′(cosθ,sinθ,0),
其中θ为B′C与CD的夹角,θ∈[0,2π),
∴AB′在运动过程中的向量, =(﹣cosθ,﹣sinθ,1),| |= ,
设 与 所成夹角为α∈[0, ],
则cosα= = |sinθ|∈[0, ],
∴α∈[ , ],∴③正确,④错误.
设 与 所成夹角为β∈[0, ],
cosβ= = = |cosθ|,
当 与 夹角为60°时,即α= ,
|sinθ|= = = ,
∵cos2θ+sin2θ=1,∴cosβ= |cosθ|= ,
∵β∈[0, ],∴β= ,此时 与 的夹角为60°,
∴②正确,①错误.
故答案为:②③.
9.(2015·四川,14)如图,四边形ABCD和ADPQ均为正方形,它们所在的平面互相垂直,动点M在线段PQ上,E、F分别为AB、BC的中点.设异面直线EM与AF所成的角为θ,则cos θ的最大值为________.
9. [建立空间直角坐标系如图所示,
设AB=1,则=,E,
设M(0,y,1)(0≤y≤1),则=,∴cos θ==-.
设异面直线所成的角为α,则cos α=|cos θ|==·,
令t=1-y,则y=1-t,
∵0≤y≤1,∴0≤t≤1,
那么cos α=|cos θ|=·==,
令x=,∵0≤t≤1,∴x≥1,那么cos α=,
又∵z=9x2-8x+4在[1,+∞)上单增,∴x=1,zmin=5,
此时cos α的最大值=·=·=.]
10.(2018全国Ⅰ,18)如图,四边形ABCD为正方形,E,F分别为AD,BC的中点,以DF
为折痕把△DFC折起,使点C到达点P的位置,且PF⊥BF.
(1)证明:平面PEF⊥平面ABFD;
(2)求DP与平面ABFD所成角的正弦值.
10.(1)由已知可得,BF⊥PF,BF⊥EF,又PF∩EF=F,所以BF⊥平面PEF.
又BF⊂平面ABFD,所以平面PEF⊥平面ABFD.
(2)作PH⊥EF,垂足为H.由(1)得,PH⊥平面ABFD.
以H为坐标原点,HF的方向为y轴正方向,|BF|为单位长,建立如图所示的空间直角坐标系H−xyz.
由(1)可得,DE⊥PE.又DP=2,DE=1,所以PE=3.又PF=1,EF=2,故PE⊥PF.
可得PH=32,EH=32.
则H(0,0,0),P(0,0,32),D(-1,-32,0),DP=(1,32,32), HP=(0,0,32)为平面ABFD的法向量.
设DP与平面ABFD所成角为θ,则sinθ=|HP⋅DP|HP|⋅|DP||=343=34.
所以DP与平面ABFD所成角的正弦值为34.
11.(2018全国Ⅱ,20)如图,在三棱锥P−ABC中,AB=BC=22,PA=PB=PC=AC=4,O为AC的中点.
(1)证明:PO⊥平面ABC;
(2)若点M在棱BC上,且二面角为,求与平面所成角的正弦值.
11.(1)因为AP=CP=AC=4,O为AC的中点,所以OP⊥AC,且OP=23.
连结OB.因为AB=BC=22AC,所以△ABC为等腰直角三角形,且OB⊥AC,OB=12AC=2.
由OP2+OB2=PB2知,OP⊥OB.
由OP⊥OB,OP⊥AC知PO⊥平面ABC.
(2)如图,以为坐标原点,的方向为轴正方向,建立空间直角坐标系.
由已知得取平面的法向量.
设,则.
设平面的法向量为.
由得,可取,
所以.由已知得.
所以.解得(舍去),.
所以.又,所以.
所以与平面所成角的正弦值为.
12.(2018全国Ⅲ,19)如图,边长为2的正方形ABCD所在的平面与半圆弧CD所在平面垂直,M是CD上异于C,D的点.
(1)证明:平面AMD⊥平面BMC;
(2)当三棱锥M−ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.
12.(1)由题设知,平面CMD⊥平面ABCD,交线为CD.因为BC⊥CD,BC⊂平面ABCD,所以BC⊥平面CMD,故BC⊥DM.
因为M为CD上异于C,D的点,且DC为直径,所以 DM⊥CM.
又 BC∩CM=C,所以DM⊥平面BMC.
而DM⊂平面AMD,故平面AMD⊥平面BMC.
(2)以D为坐标原点,DA的方向为x轴正方向,建立如图所示的空间直角坐标系D−xyz.
当三棱锥M−ABC体积最大时,M为CD的中点.
由题设得D(0,0,0),A(2,0,0),B(2,2,0),C(0,2,0),M(0,1,1),
AM=(-2,1,1),AB=(0,2,0),DA=(2,0,0)
设n=(x,y,z)是平面MAB的法向量,则
n⋅AM=0,n⋅AB=0.即-2x+y+z=0,2y=0.
可取n=(1,0,2).
DA是平面MCD的法向量,因此
cosn,DA=n⋅DA|n||DA|=55,
sinn,DA=255,
所以面MAB与面MCD所成二面角的正弦值是255.
13.(2018天津,17)如图, 且AD=2BC, , 且EG=AD, 且CD=2FG, ,DA=DC=DG=2.
(I)若M为CF的中点,N为EG的中点,求证: MN∥平面CDE;
(II)求二面角的正弦值;
(III)若点P在线段DG上,且直线BP与平面ADGE所成的角为60°,求线段DP的长.
13.依题意,可以建立以D为原点,
分别以, , 的方向为x轴,y轴,z轴的正方向的空间直角坐标系(如图),
可得D(0,0,0),A(2,0,0),B(1,2,0),C(0,2,0),
E(2,0,2),F(0,1,2),G(0,0,2),M(0, ,1),N(1,0,2).
(Ⅰ)依题意=(0,2,0),=(2,0,2).
设n0=(x,y,z)为平面CDE的法向量,
则 即
不妨令z=–1,可得n0=(1,0,–1).
又=(1, ,1),可得,
又因为直线MN平面CDE,所以MN∥平面CDE.
(Ⅱ)依题意,可得=(–1,0,0),, =(0,–1,2).
设n=(x,y,z)为平面BCE的法向量,
则 即
不妨令z=1,可得n=(0,1,1).
设m=(x,y,z)为平面BCF的法向量,
则 即
不妨令z=1,可得m=(0,2,1).
因此有cos=,于是sin=.
所以,二面角E–BC–F的正弦值为.
(Ⅲ)设线段DP的长为h(h∈[0,2]),则点P的坐标为(0,0,h),
可得.
易知, =(0,2,0)为平面ADGE的一个法向量,
故,
由题意,可得=sin60°=,解得h=∈[0,2].
所以线段的长为.
14.(2018浙江,19)如图,已知多面体ABCA1B1C1,A1A,B1B,C1
C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2.
(Ⅰ)证明:AB1⊥平面A1B1C1;
(Ⅱ)求直线AC1与平面ABB1所成的角的正弦值.
14.方法一:
(Ⅰ)由AB=2,AA1=4,BB1=2,AA1⊥AB,BB1⊥AB得AB1=A1B1=22,
所以A1B12+AB12=AA12.
故AB1⊥A1B1.
由BC=2,BB1=2,CC1=1, BB1⊥BC,CC1⊥BC得B1C1=5,
由AB=BC=2,∠ABC=120°得AC=23,
由CC1⊥AC,得AC1=13,所以AB12+B1C12=AC12,故AB1⊥B1C1.
因此AB1⊥平面A1B1C1.
(Ⅱ)如图,过点C1作C1D⊥A1B1,交直线A1B1于点D,连结AD.
由AB1⊥平面A1B1C1得平面A1B1C1⊥平面ABB1,
由C1D⊥A1B1得C1D⊥平面ABB1,
所以∠C1AD是AC1与平面ABB1所成的角.学科.网
由B1C1=5,A1B1=22,A1C1=21得cos∠C1A1B1=67,sin∠C1A1B1=17,
所以C1D=3,故sin∠C1AD=C1DAC1=3913.
因此,直线AC1与平面ABB1所成的角的正弦值是3913.
方法二:
(Ⅰ)如图,以AC的中点O为原点,分别以射线OB,OC为x,y轴的正半轴,建立空间直角坐标系O-xyz.
由题意知各点坐标如下:
A(0,-3,0),B(1,0,0),A1(0,-3,4),B1(1,0,2),C1(0,3,1),
因此AB1=(1,3,2),A1B1=(1,3,-2),A1C1=(0,23,-3),
由AB1⋅A1B1=0得AB1⊥A1B1.
由AB1⋅A1C1=0得AB1⊥A1C1.
所以AB1⊥平面A1B1C1.
(Ⅱ)设直线AC1与平面ABB1所成的角为θ.
由(Ⅰ)可知AC1=(0,23,1),AB=(1,3,0),BB1=(0,0,2),
设平面ABB1的法向量n=(x,y,z).
由n⋅AB=0,n⋅BB1=0,即x+3y=0,2z=0,可取n=(-3,1,0).
所以sinθ=|cosAC1,n|=|AC1⋅n||AC1|⋅|n|=3913.
因此,直线AC1与平面ABB1所成的角的正弦值是3913.
15.(2018江苏,22)如图,在正三棱柱ABC-A1B1C1中,AB=AA1=2,点P,Q分别为A1B1,BC的中点.
(1)求异面直线BP与AC1所成角的余弦值;
(2)求直线CC1与平面AQC1所成角的正弦值.
15.如图,在正三棱柱ABC−A1B1C1中,设AC,A1C1的中点分别为O,O1,则OB⊥OC,OO1⊥OC,
OO1⊥OB,以{OB,OC,OO1}为基底,建立空间直角坐标系O−xyz.
因为AB=AA1=2,
所以A(0,-1,0),B(3,0,0),C(0,1,0),A1(0,-1,2),B1(3,0,2),C1(0,1,2).
(1)因为P为A1B1的中点,所以P(32,-12,2),
从而BP=(-32,-12,2),AC1=(0,2,2),
故|cosBP,AC1|=|BP⋅AC1||BP|⋅|AC1|=|-1+4|5×22=31020.
因此,异面直线BP与AC1所成角的余弦值为31020.
(2)因为Q为BC的中点,所以Q(32,12,0),
因此AQ=(32,32,0),AC1=(0,2,2),CC1=(0,0,2).
设n=(x,y,z)为平面AQC1的一个法向量,
则AQ⋅n=0,AC1⋅n=0,即32x+32y=0,2y+2z=0.
不妨取n=(3,-1,1),
设直线CC1与平面AQC1所成角为θ,
则sinθ=|cosCC1,n|=|CC1⋅n||CC1|⋅|n|=25×2=55,
所以直线CC1与平面AQC1所成角的正弦值为55.
16.(2018北京,16)如图,在三棱柱ABC−A1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=5,AC=AA1=2.
(1)求证:AC⊥平面BEF;
(2)求二面角B−CD−C1的余弦值;
(3)证明:直线FG与平面BCD相交.
16.(Ⅰ)在三棱柱ABC-A1B1C1中,
∵CC1⊥平面ABC,
∴四边形A1ACC1为矩形.
又E,F分别为AC,A1C1的中点,
∴AC⊥EF.
∵AB=BC.
∴AC⊥BE,
∴AC⊥平面BEF.
(Ⅱ)由(I)知AC⊥EF,AC⊥BE,EF∥CC1.
又CC1⊥平面ABC,∴EF⊥平面ABC.
∵BE⊂平面ABC,∴EF⊥BE.
如图建立空间直角坐称系E-xyz.
由题意得B(0,2,0),C(-1,0,0),D(1,0,1),F(0,0,2),G(0,2,1).
∴CD=(2 , 0 , 1) , CB=(1 , 2 , 0) ,
设平面BCD的法向量为n=(a , b , c),
∴n⋅CD=0n⋅CB=0,∴2a+c=0a+2b=0,
令a=2,则b=-1,c=-4,
∴平面BCD的法向量n=(2 , -1 , -4),
又∵平面CDC1的法向量为EB=(0 , 2 , 0),
∴cos=n⋅EB|n||EB|=-2121.
由图可得二面角B-CD-C1为钝角,所以二面角B-CD-C1的余弦值为-2121.
(Ⅲ)平面BCD的法向量为n=(2 , -1 , -4),∵G(0,2,1),F(0,0,2),
∴GF=(0 , -2 , 1),∴n⋅GF=-2,∴n与GF不垂直,
∴GF与平面BCD不平行且不在平面BCD内,∴GF与平面BCD相交.
17.(2017•山东,17)如图,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是 的中点.(12分)
(Ⅰ)设P是 上的一点,且AP⊥BE,求∠CBP的大小;
(Ⅱ)当AB=3,AD=2时,求二面角E﹣AG﹣C的大小.
17..(Ⅰ)∵AP⊥BE,AB⊥BE,且AB,AP⊂平面ABP,AB∩AP=A,
∴BE⊥平面ABP,又BP⊂平面ABP,
∴BE⊥BP,又∠EBC=120°,
因此∠CBP=30°;
(Ⅱ)解法一、
取 的中点H,连接EH,GH,CH,
∵∠EBC=120°,∴四边形BEGH为菱形,
∴AE=GE=AC=GC= .
取AG中点M,连接EM,CM,EC,
则EM⊥AG,CM⊥AG,
∴∠EMC为所求二面角的平面角.
又AM=1,∴EM=CM= .
在△BEC中,由于∠EBC=120°,
由余弦定理得:EC2=22+22﹣2×2×2×cos120°=12,
∴ ,因此△EMC为等边三角形,
故所求的角为60°.
解法二、以B为坐标原点,分别以BE,BP,BA所在直线为x,y,z轴建立空间直角坐标系.
由题意得:A(0,0,3),E(2,0,0),G(1, ,3),C(﹣1, ,0),
故 , , .
设 为平面AEG的一个法向量,
由 ,得 ,取z1=2,得 ;
设 为平面ACG的一个法向量,
由 ,可得 ,取z2=﹣2,得 .
∴cos< >= .
∴二面角E﹣AG﹣C的大小为60°.
18.(2017·天津,17)如图,在三棱锥P﹣ABC中,PA⊥底面ABC,∠BAC=90°.点D,E,N分别为棱PA,PC,BC的中点,M是线段AD的中点,PA=AC=4,AB=2.
(Ⅰ)求证:MN∥平面BDE;
(Ⅱ)求二面角C﹣EM﹣N的正弦值;
(Ⅲ)已知点H在棱PA上,且直线NH与直线BE所成角的余弦值为 ,求线段AH
的长.
18.(Ⅰ)证明:取AB中点F,连接MF、NF,
∵M为AD中点,∴MF∥BD,
∵BD⊂平面BDE,MF⊄平面BDE,∴MF∥平面BDE.
∵N为BC中点,∴NF∥AC,
又D、E分别为AP、PC的中点,∴DE∥AC,则NF∥DE.
∵DE⊂平面BDE,NF⊄平面BDE,∴NF∥平面BDE.
又MF∩NF=F.
∴平面MFN∥平面BDE,则MN∥平面BDE;
(Ⅱ)解:∵PA⊥底面ABC,∠BAC=90°.
∴以A为原点,分别以AB、AC、AP所在直线为x、y、z轴建立空间直角坐标系.
∵PA=AC=4,AB=2,
∴A(0,0,0),B(2,0,0),C(0,4,0),M(0,0,1),N(1,2,0),E(0,2,2),
则 , ,
设平面MEN的一个法向量为 ,
由 ,得 ,取z=2,得 .
由图可得平面CME的一个法向量为 .
∴cos< >= .
∴二面角C﹣EM﹣N的余弦值为 ,则正弦值为 ;
(Ⅲ)解:设AH=t,则H(0,0,t), , .
∵直线NH与直线BE所成角的余弦值为 ,
∴|cos< >|=| |=| |= .
解得:t=4.
∴当H与P重合时直线NH与直线BE所成角的余弦值为 ,此时线段AH的长为4.
19.(2017•浙江,19)如图,已知四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点.
(Ⅰ)证明:CE∥平面PAB;
(Ⅱ)求直线CE与平面PBC所成角的正弦值.
19.(Ⅰ)∵四棱锥P﹣ABCD,△PAD是以AD为斜边的等腰直角三角形,BC∥AD,CD⊥AD,PC=AD=2DC=2CB,E为PD的中点,∴以D为原点,DA为x轴,DC为y轴,过D作平面ABCD的垂线为z轴,建立空间直角系,设PC=AD=2DC=2CB=2,
则C(0,1,0),D(0,0,0),P(1,0,1),E( ),A(2,0,0),B(1,1,0),
=( ), =(1,0,﹣1), =(0,1,﹣1),
设平面PAB的法向量 =(x,y,z),
则 ,取z=1,得 =(1,1,1),
∵ = =0,CE⊄平面PAB,
∴CE∥平面PAB.
解:(Ⅱ) =(﹣1,1,﹣1),设平面PBC的法向量 =(a,b,c),
则 ,取b=1,得 =(0,1,1),
设直线CE与平面PBC所成角为θ,
则sinθ=|cos< >|= = = .
∴直线CE与平面PBC所成角的正弦值为 .
20.(2016·全国Ⅱ,19)如图,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=,EF交BD于点H.将△DEF沿EF折到△D′EF的位置.OD′=.
(1)证明:D′H⊥平面ABCD;
(2)求二面角B-D′A-C的正弦值.
20.(1)证明由已知得AC⊥BD,AD=CD.又由AE=CF得=,故AC∥EF.
因此EF⊥HD,从而EF⊥D′H.由AB=5,AC=6得DO=BO==4.
由EF∥AC得==.所以OH=1,D′H=DH=3.
于是D′H2+OH2=32+12=10=D′O2,故D′H⊥OH.又D′H⊥EF,而OH∩EF=H,
所以D′H⊥平面ABCD.
(2)解如图,以H为坐标原点,的方向为x轴正方向,建立空间直角坐标系H-xyz.则H(0,0,0),A(-3,-1,0),
B(0,-5,0),C(3,-1,0),D′(0,0,3),=(3,-4,0),=(6,0,0),=(3,1,3).
设m=(x1,y1,z1)是平面ABD′的法向量,则即
所以可取m=(4,3,-5).
设n=(x2,y2,z2)是平面ACD′的法向量,则即
所以可取n=(0,-3,1).
于是cos〈m,n〉===-.sin〈m,n〉=.
因此二面角B-D′A-C的正弦值是.
21.(2015·陕西,18)如图1,在直角梯形ABCD中,AD∥BC,∠BAD=,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到△A1BE的位置,如图2.
(1)证明:CD⊥平面A1OC;
(2)若平面A1BE⊥平面BCDE,求平面A1BC与平面A1CD夹角的余弦值.
21.(1)证明在图1中,因为AB=BC=1,AD=2,E是AD的中点,∠BAD=,所以BE⊥AC,
图1
即在图2中,BE⊥OA1,BE⊥OC,且A1O∩OC=O,
图2
从而BE⊥平面A1OC,
又在直角梯形ABCD中,AD∥BC,BC=AD,E为AD中点,所以BC綉ED,
所以四边形BCDE为平行四边形,故有CD∥BE,所以CD⊥平面A1OC.
(2)解由已知,平面A1BE⊥平面BCDE,又由(1)知,BE⊥OA1,BE⊥OC,
所以∠A1OC为二面角A1BEC的平面角,所以∠A1OC=,
如图,以O为原点,建立空间直角坐标系,
因为A1B=A1E=BC=ED=1,BC∥ED,
所以B,E,A1,C,得=,
=,==(-,0,0),
设平面A1BC的法向量n1=(x1,y1,z1),平面A1CD的法向量n2=(x2,y2,z2),平面A1BC与平面A1CD夹角为θ,则得取n1=(1,1,1);得
取n2=(0,1,1),从而cosθ=|cos|==,
即平面A1BC与平面A1CD夹角的余弦值为.
22.(2015·天津,17)如图,在四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB⊥AC,AB=1,AC=AA1=2,AD=CD=,且点M和N分别为B1C和D1D的中点.
(1)求证:MN∥平面ABCD;
(2)求二面角D1-AC-B1的正弦值;
(3)设E为棱A1B1上的点,若直线NE和平面ABCD所成角的正弦值为,求线段A1E的长.
22.如图,以A为原点建立空间直角坐标系,
依题意可得A(0,0,0),B(0,1,0),C(2,0,0),D(1,-2,0),
A1(0,0,2),B1(0,1,2),C1(2,0,2),D1(1,-2,2),又因为M,N分别为B1C和D1D的中点,
得M,N(1,-2,1).
(1)证明依题意,可得n=(0,0,1)为平面ABCD的一个法向量,=,由此可得·n=0,又因为直线MN⊄平面ABCD,所以MN∥平面ABCD.
(2)解 =(1,-2,2),=(2,0,0),设n1=(x,y,z)为平面ACD1的法向量,
则即
不妨设z=1,可得n1=(0,1,1).
设n2=(x,y,z)为平面ACB1的法向量,则
又=(0,1,2),得不妨设z=1,可得n2=(0,-2,1).
因此有cos〈n1,n2〉==-,于是sin〈n1,n2〉=.
所以,二面角D1ACB1的正弦值为.
(3)解 依题意,可设=λ,其中λ∈[0,1],则E(0,λ,2),从而=(-1,λ+2,1),又n=(0,0,1)为平面ABCD的一个法向量,
由已知,得cos〈,n〉===,
整理得λ2+4λ-3=0,又因为λ∈[0,1],解得λ=-2,所以,线段A1E的长为-2.
23.(2015·安徽,19)如图所示,在多面体A1B1D1DCBA,四边形AA1B1B,ADD1A1,ABCD均为正方形,E为B1D1的中点,过A1,D,E的平面交CD1于F.
(1)证明:EF∥B1C.
(2)求二面角EA1DB1的余弦值.
23.(1)证明 由正方形的性质可知A1B1∥AB∥DC,且A1B1=AB=DC,所以四边形A1B1CD为平行四边形,从而B1C∥A1D,又A1D⊂面A1DE,B1C⊄面A1DE,于是B1C∥面A1DE.又B1C⊂面B1CD1.面A1DE∩面B1CD1=EF,所以EF∥B1C.
(2)解 因为四边形AA1B1B,ADD1A1,ABCD均为正方形,所以AA1⊥AB,AA1⊥AD,AB⊥AD且AA1=AB=AD.以A为原点,分别以,,为x轴,y轴和z轴单位正向量建立如图所示的空间直角坐标系,可得点的坐标A(0,0,0),B(1,0,0),D(0,1,0),A1(0,0,1),B1(1,0,1),D1(0,1,1),而E点为B1D1的中点,所以E点的坐标为.
设面A1DE的法向量n1=(r1,s1,t1),而该面上向量=,=(0,1,-1),由n1⊥.
n1⊥得r1,s1,t1应满足的方程组(-1,1,1)为其一组解,
所以可取n1=(-1,1,1).
设面A1B1CD的法向量n2=(r2,s2,t2),而该面上向量=(1,0,0),=(0,1,-1),由此同理可得n2=(0,1,1).
所以结合图形知二面角EA1DB1的余弦值为==.
24.(2015·重庆,19)如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=.D,E分别为线段AB,BC上的点,且CD=DE=,CE=2EB=2.
(1)证明:DE⊥平面PCD;
(2)求二面角APDC的余弦值.
24.(1)证明 由PC⊥平面ABC,DE⊂平面ABC,故PC⊥DE.
由CE=2,CD=DE=得△CDE为等腰直角三角形,故CD⊥DE.
由PC∩CD=C,DE垂直于平面PCD内两条相交直线,故DE⊥平面PCD.
(2)解 由(1)知,△CDE为等腰直角三角形,∠DCE=,如图,过D作DF垂直CE于F,易知DF=FC=FE=1,又已知EB=1,故FB=2.
由∠ACB=得DF∥AC,==,故AC=DF=.
以C为坐标原点,分别以,,的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0),P(0,0,3),A,E(0,2,0),D(1,1,0),=(1,-1,0),=(-1,-1,3),=.
设平面PAD的法向量为n1=(x1,y1,z1),
由n1·=0,n1·=0,得故可取n1=(2,1,1).
由(1)可知DE⊥平面PCD,故平面PCD的法向量n2可取为,即n2=(1,-1,0).
从而法向量n1,n2的夹角的余弦值为cos〈n1,n2〉==,
故所求二面角APDC的余弦值为.
25.(2015·北京,17)如图,在四棱锥AEFCB中,△AEF为等边三角形,平面AEF⊥平面EFCB,EF∥BC,BC=4,EF=2a,∠EBC=∠FCB=60°,O为EF的中点.
(1) 求证:AO⊥BE;
(2) 求二面角FAEB的余弦值;
(3)若BE⊥平面AOC,求a的值.
25.(1)证明 因为△AEF是等边三角形,O为EF的中点,所以AO⊥EF.
又因为平面AEF⊥平面EFCB.AO⊂平面AEF,所以AO⊥平面EFCB.所以AO⊥BE.
(2)解 取BC中点G,连接OG.由题设知EFCB是等腰梯形,所以OG⊥EF.
由(1)知AO⊥平面EFCB.又OG⊂平面EFCB,所以OA⊥OG.
如图建立空间直角坐标系Oxyz,
则E(a,0,0),A(0,0,a),B(2,(2-a),0),=(-a,0,a),=(a-2,(a-2),0).
设平面AEB的法向量为n=(x,y,z),则即
令z=1,则x=,y=-1,于是n=(,-1,1).
平面AEF的法向量为p=(0,1,0).所以cos〈n,p〉==-.
由题知二面角FAEB为钝角,所以它的余弦值为-.
(3)解 因为BE⊥平面AOC,所以BE⊥OC,即·=0,因为=(a-2,(a-2),0),
=(-2,(2-a),0),所以·=-2(a-2)-3(a-2)2.
由·=0及0