数学文·湖北省部分重点中学联考2016-2017学年高二上学期期中数学试卷（文科） Word版含解析]x 23页

‎2016-2017学年湖北省部分重点中学联考高二（上）期中数学试卷（文科）‎ ‎　‎ 一、选择题（5×12=60分）‎ ‎1．下列命题正确的是（　　）‎ A．经过三点确定一个平面 B．经过一条直线和一个点确定一个平面 C．四边形确定一个平面 D．两两相交且不共点的三条直线确定一个平面 ‎2．为了了解1200名学生对学校某项教改试验的意见，打算从中抽取一个容量为30的样本，考虑采用系统抽样，则分段的间隔（抽样距）K为（　　）‎ A．40 B．30 C．20 D．12‎ ‎3．已知直线l⊥平面α，直线m⊂平面β，给出下列命题 ‎①α∥β=l⊥m；‎ ‎②α⊥β⇒l∥m；‎ ‎③l∥m⇒α⊥β；‎ ‎④l⊥m⇒α∥β．‎ 其中正确命题的序号是（　　）‎ A．①②③ B．②③④ C．①③ D．②④‎ ‎4．某程序框图如图所示，若输出的S=57，则判断框内为（　　）‎ A．k＞4？ B．k＞5？ C．k＞6？ D．k＞7？‎ ‎5．有5根细木棍，长度分别为1、3、5、7、9（cm），从中任取三根，能搭成三角形的概率为（（　　）‎ A． B． C． D．‎ ‎6．如图是歌手大奖赛中，七位评委为甲，乙两名选手打出的分数的茎叶图（其中m为数字0﹣9中的一个），去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为a1，a2，则一定有（　　）‎ A．a1＞a2 B．a2＞a1‎ C．a1=a2 D．a1，a2的大小不确定 ‎7．某人5次上班途中所花的时间（单位：分钟）分别为x，y，10，11，9．已知这组数据的平均数为10，方差为2，则|x﹣y|的值为（　　）‎ A．1 B．2 C．3 D．4‎ ‎8．两条异面直线a，b所成的角是60°，A为空间一定点，则过点A作一条与直线a，b均成60°的直线，这样的直线能作几条（　　）‎ A．1条 B．2条 C．3条 D．4条 ‎9．如图是正方体的平面展开图．在这个正方体中，‎ ‎①BM与ED平行；‎ ‎②CN与BE是异面直线；‎ ‎③CN与BM成60°角；‎ ‎④DM与BN垂直．‎ 以上四个命题中，正确命题的序号是（　　）‎ A．①②③ B．②④ C．③④ D．②③④‎ ‎10．如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，点P在线段AD1上运动，给出以下四个命题：‎ ‎①异面直线C1P与CB1所成的角为定值；‎ ‎②二面角P﹣BC1﹣D的大小为定值；‎ ‎③三棱锥D﹣BPC1的体积为定值；‎ 其中真命题的个数为（　　）‎ A．0 B．1 C．2 D．3‎ ‎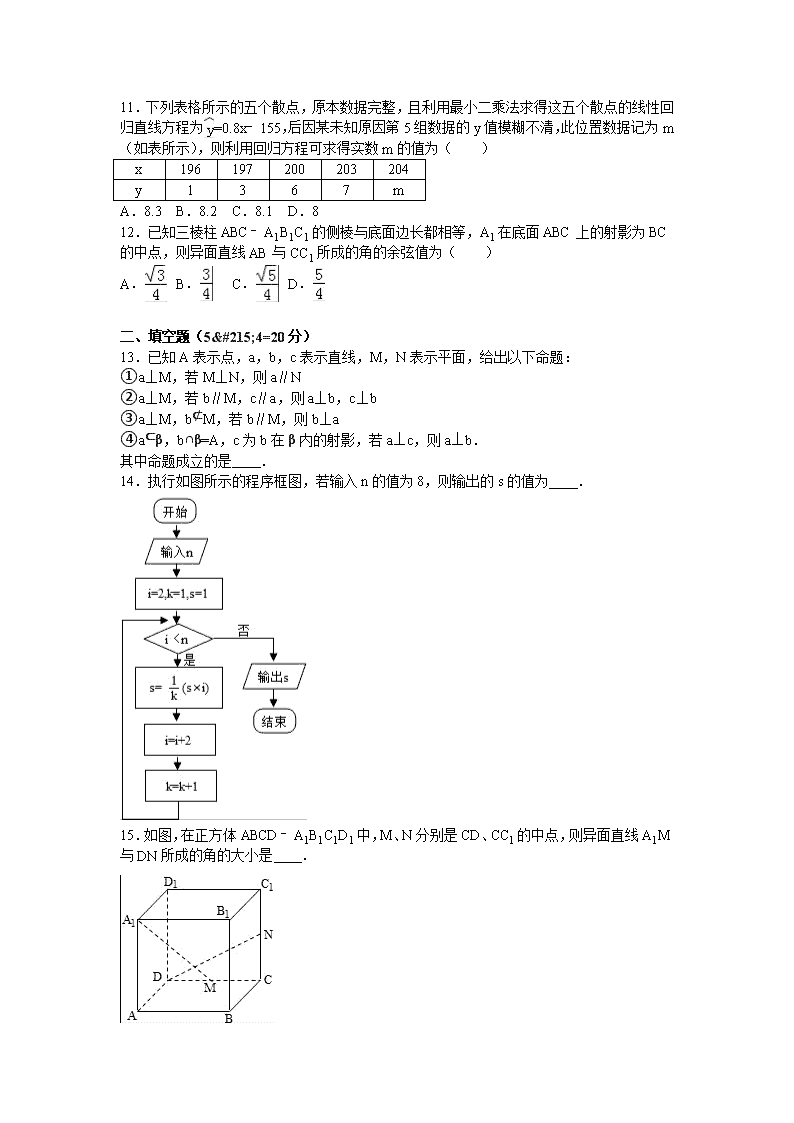11．下列表格所示的五个散点，原本数据完整，且利用最小二乘法求得这五个散点的线性回归直线方程为=0.8x﹣155，后因某未知原因第5组数据的y值模糊不清，此位置数据记为m（如表所示），则利用回归方程可求得实数m的值为（　　）‎ x ‎196‎ ‎197‎ ‎200‎ ‎203‎ ‎204‎ y ‎1‎ ‎3‎ ‎6‎ ‎7‎ m A．8.3 B．8.2 C．8.1 D．8‎ ‎12．已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等，A1在底面ABC上的射影为BC的中点，则异面直线AB与CC1所成的角的余弦值为（　　）‎ A． B． C． D．‎ ‎　‎ 二、填空题（5×4=20分）‎ ‎13．已知A表示点，a，b，c表示直线，M，N表示平面，给出以下命题：‎ ‎①a⊥M，若M⊥N，则a∥N ‎ ‎②a⊥M，若b∥M，c∥a，则a⊥b，c⊥b ‎③a⊥M，b⊄M，若b∥M，则b⊥a ‎④a⊂β，b∩β=A，c为b在β内的射影，若a⊥c，则a⊥b．‎ 其中命题成立的是　　．‎ ‎14．执行如图所示的程序框图，若输入n的值为8，则输出的s的值为　　．‎ ‎15．如图，在正方体ABCD﹣A1B1C1D1中，M、N分别是CD、CC1的中点，则异面直线A1M与DN所成的角的大小是　　．‎ ‎16．甲、乙两艘轮船都要停靠在同一个泊位，它们可能在一昼夜的任意时刻到达．甲、乙两船停靠泊位的时间分别为4小时与2小时，则有一艘船停靠泊位时必需等待一段时间的概率为　　．‎ ‎　‎ 三、解答题（10+12×5=70分）‎ ‎17．某市规定，高中学生在校期间须参加不少于80小时的社区服务才合格．某校随机抽取20位学生参加社区服务的数据，按时间段[75，80），[80，85），[85，90），[90，95），[95，100]（单位：小时）进行统计，其频率分布直方图如图所示．‎ ‎（Ⅰ）求抽取的20人中，参加社区服务时间不少于90小时的学生人数；‎ ‎（Ⅱ）从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生的参加社区服务时间在同一时间段内的概率．‎ ‎18．已知：四棱锥P﹣ABCD的底面为正方形，PA⊥底面ABCD，E、F分别为AB、PD的中点，PA=a，∠PDA=45°‎ ‎（1）求证：AF∥平面PCE； ‎ ‎（2）求证：平面PCE⊥平面PCD；‎ ‎（3）求点D到平面PCE的距离．‎ ‎19．某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．‎ ‎（1）求图中a的值；‎ ‎（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．‎ 分数段 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ x：y ‎1：1‎ ‎2：1‎ ‎3：4‎ ‎4：5‎ ‎20．已知四棱锥P﹣GBCD中（如图），PG⊥平面GBCD，GD∥BC，GD=BC，且BG⊥GC，GB=GC=2，E是BC的中点，PG=4‎ ‎（Ⅰ）求异面直线GE与PC所成角的余弦值；‎ ‎（Ⅱ）若F点是棱PC上一点，且DF⊥GC，PF：FC=k，求k的值．‎ ‎21．等边三角形ABC的边长为2沿平行于BC的线段PQ折起，使平面APQ⊥平面PBCQ，设点A到直线PQ的距离为x，AB的长为d．‎ ‎（Ⅰ）x为何值时，d2取得最小值，最小值是多少；‎ ‎（Ⅱ）若∠BAC=θ，求cosθ的最小值．‎ ‎22．如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC的中点，F在棱AC上，且AF=3FC．‎ ‎（1）求三棱锥D﹣ABC的表面积；‎ ‎（2）求证AC⊥平面DEF；‎ ‎（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由．‎ ‎　‎ ‎2016-2017学年湖北省部分重点中学联考高二（上）期中数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（5×12=60分）‎ ‎1．下列命题正确的是（　　）‎ A．经过三点确定一个平面 B．经过一条直线和一个点确定一个平面 C．四边形确定一个平面 D．两两相交且不共点的三条直线确定一个平面 ‎【考点】平面的基本性质及推论．‎ ‎【分析】根据公理2以及推论判断A、B、D，再根据空间四边形判断C．‎ ‎【解答】解：A、根据公理2知，必须是不共线的三点确定一个平面，故A不对；‎ B、根据一条直线和直线外的一点确定一个平面知，故B不对；‎ C、比如空间四边形则不是平面图形，故C不对；‎ D、两两相交且不共点的三条直线，则三个交点不共线，故它们确定一个平面，由公理1知三条直线都在此平面内，故D正确．‎ 故选D．‎ ‎　‎ ‎2．为了了解1200名学生对学校某项教改试验的意见，打算从中抽取一个容量为30的样本，考虑采用系统抽样，则分段的间隔（抽样距）K为（　　）‎ A．40 B．30 C．20 D．12‎ ‎【考点】系统抽样方法．‎ ‎【分析】系统抽样中，分段的间隔（抽样距）=‎ ‎【解答】解：抽样距==40．‎ 故选 A ‎　‎ ‎3．已知直线l⊥平面α，直线m⊂平面β，给出下列命题 ‎①α∥β=l⊥m；‎ ‎②α⊥β⇒l∥m；‎ ‎③l∥m⇒α⊥β；‎ ‎④l⊥m⇒α∥β．‎ 其中正确命题的序号是（　　）‎ A．①②③ B．②③④ C．①③ D．②④‎ ‎【考点】平面与平面之间的位置关系．‎ ‎【分析】由两平行平面中的一个和直线垂直，另一个也和平面垂直得直线l⊥平面β，再利用面面垂直的判定可得①为真命题；‎ 当直线与平面都和同一平面垂直时，直线与平面可以平行，也可以在平面内，故②为假命题；‎ 由两平行线中的一条和平面垂直，另一条也和平面垂直得直线m⊥平面α，再利用面面垂直的判定可得③为真命题；‎ 当直线与平面都和同一平面垂直时，直线与平面可以平行，也可以在平面内，如果直线m在平面α内，则有α和β相交于m，故④为假命题．‎ ‎【解答】解：l⊥平面α且α∥β可以得到直线l⊥平面β，又由直线m⊂平面β，所以有l⊥m；即①为真命题；‎ 因为直线l⊥平面α且α⊥β可得直线l平行与平面β或在平面β内，又由直线m⊂平面β，所以l与m，可以平行，相交，异面；故②为假命题；‎ 因为直线l⊥平面α且l∥m可得直线m⊥平面α，又由直线m⊂平面β可得α⊥β；即③为真命题；‎ 由直线l⊥平面α以及l⊥m可得直线m平行与平面α或在平面α内，又由直线m⊂平面β得α与β可以平行也可以相交，即④为假命题．‎ 所以真命题为①③．‎ 故选 C．‎ ‎　‎ ‎4．某程序框图如图所示，若输出的S=57，则判断框内为（　　）‎ A．k＞4？ B．k＞5？ C．k＞6？ D．k＞7？‎ ‎【考点】程序框图．‎ ‎【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输入S的值，条件框内的语句是决定是否结束循环，模拟执行程序即可得到答案．‎ ‎【解答】解：程序在运行过程中各变量值变化如下表：‎ K S 是否继续循环 循环前 1 1/‎ 第一圈 2 4 是 第二圈 3 11 是 第三圈 4 26 是 第四圈 5 57 否 故退出循环的条件应为k＞4‎ 故答案选A．‎ ‎　‎ ‎5．有5根细木棍，长度分别为1、3、5、7、9（cm），从中任取三根，能搭成三角形的概率为（（　　）‎ A． B． C． D．‎ ‎【考点】列举法计算基本事件数及事件发生的概率．‎ ‎【分析】由组合数公式可得从5根木棒中任取3根的情况数目，由三角形的三边关系分析可得取出的三根可以搭成三角形的情况数目，由等可能事件的概率公式，计算可得答案．‎ ‎【解答】解：根据题意，从5根木棒中任取3根，有C53=10种情况，‎ 其中能构撘成三角形的有3、5、7，3、7、9，5、7、9，共3种情况，‎ 则能搭成三角形的概率为；‎ 故选D．‎ ‎　‎ ‎6．如图是歌手大奖赛中，七位评委为甲，乙两名选手打出的分数的茎叶图（其中m为数字0﹣9中的一个），去掉一个最高分和一个最低分后，甲、乙两名选手得分的平均数分别为a1，a2，则一定有（　　）‎ A．a1＞a2 B．a2＞a1‎ C．a1=a2 D．a1，a2的大小不确定 ‎【考点】众数、中位数、平均数；茎叶图．‎ ‎【分析】由题意知去掉一个最高分和一个最低分以后，两组数据都有五个数据，根据样本平均数的计算公式，代入数据可以求得甲和乙的平均分，把两个平均分进行比较，得到结果．‎ ‎【解答】解：由题意知去掉一个最高分和一个最低分以后，两组数据都有五个数据，‎ 代入数据可以求得甲和乙的平均分 ‎，‎ ‎，‎ ‎∴a2＞a1‎ 故选B．‎ ‎　‎ ‎7．某人5次上班途中所花的时间（单位：分钟）分别为x，y，10，11，9．已知这组数据的平均数为10，方差为2，则|x﹣y|的值为（　　）‎ A．1 B．2 C．3 D．4‎ ‎【考点】极差、方差与标准差．‎ ‎【分析】由题意知这组数据的平均数为10，方差为2可得到关于x，y的一个方程组，解这个方程组需要用一些技巧，因为不要直接求出x、y，只要求出|x﹣y|，利用换元法来解出结果．‎ ‎【解答】解：由题意这组数据的平均数为10，方差为2可得：x+y=20，（x﹣10）2+（y﹣10）2=8，‎ 解这个方程组需要用一些技巧，‎ 因为不要直接求出x、y，只要求出|x﹣y|，‎ 设x=10+t，y=10﹣t，由（x﹣10）2+（y﹣10）2=8得t2=4；‎ ‎∴|x﹣y|=2|t|=4，‎ 故选D．‎ ‎　‎ ‎8．两条异面直线a，b所成的角是60°，A为空间一定点，则过点A作一条与直线a，b均成60°的直线，这样的直线能作几条（　　）‎ A．1条 B．2条 C．3条 D．4条 ‎【考点】空间中直线与直线之间的位置关系．‎ ‎【分析】过P作a′∥a，b′∥b，设直线a′、b′确定的平面为α，异面直线a、b成60°角，直线a′、b′所成锐角为60°，过点P与a′、b′都成60°角的直线，可以作3条．‎ ‎【解答】解：过P作a′∥a，b′∥b，‎ 设直线a′、b′确定的平面为α，‎ ‎∵异面直线a、b成60°角，‎ ‎∴直线a′、b′所成锐角为60°．‎ ‎①当直线l在平面α内时，‎ 若直线l平分直线a′、b′所成的钝角，‎ 则直线l与a、b都成60°角；‎ ‎②当直线l与平面α斜交时，若它在平面α内的射影恰好落在直线a′、b′所成的锐角平分线上时，直线l与a、b所成角相等．‎ 此时l与a′、b′所成角的范围为[30°，90°]，适当调整l的位置，可使直线l与a、b也都成60°角，这样的直线l有两条．‎ 综上所述，过点P与a′、b′都成60°角的直线，可以作3条．‎ ‎∵a′∥a，b′∥b，∴过点P与a′、b′都成60°角的直线，与a、b也都成60°的角．‎ 故选：C．‎ ‎　‎ ‎9．如图是正方体的平面展开图．在这个正方体中，‎ ‎①BM与ED平行；‎ ‎②CN与BE是异面直线；‎ ‎③CN与BM成60°角；‎ ‎④DM与BN垂直．‎ 以上四个命题中，正确命题的序号是（　　）‎ A．①②③ B．②④ C．③④ D．②③④‎ ‎【考点】棱柱的结构特征．‎ ‎【分析】正方体的平面展开图复原为正方体，不难解答本题．‎ ‎【解答】解：由题意画出正方体的图形如图：‎ 显然①②不正确；③CN与BM成60°角，即∠ANC=60°‎ 正确；④DM⊥平面BCN，所以④正确；‎ 故选C．‎ ‎　‎ ‎10．如图，在棱长为1的正方体ABCD﹣A1B1C1D1中，点P在线段AD1上运动，给出以下四个命题：‎ ‎①异面直线C1P与CB1所成的角为定值；‎ ‎②二面角P﹣BC1﹣D的大小为定值；‎ ‎③三棱锥D﹣BPC1的体积为定值；‎ 其中真命题的个数为（　　）‎ A．0 B．1 C．2 D．3‎ ‎【考点】棱柱的结构特征．‎ ‎【分析】对于①由题意及图形利用异面直线所成角的概念及求异面直线间的方法及可求解；‎ 对于②由题意及平面具有延展性可知实质为平面ABC1D1与平面BDC1所成的二面角；‎ 对于③由题意及三棱锥的体积的算法中可以进行顶点可以轮换性求解体积，和点P的位置及直线AD1与平面BDC1的位置即可判断正误．‎ ‎【解答】解：对于①因为在棱长为1的正方体ABCD﹣A1B1C1D1中，‎ 点P在线段AD1上运动，有正方体的及题意易有B1C⊥平面ABC1D1，‎ 而C1P⊂平面ABC1D1，所以B1C⊥C1P，‎ 故这两个异面直线所成的角为定值90°，所以①正确；‎ 对于②因为二面角P﹣BC1﹣D的大小，‎ 实质为平面ABC1D1与平面BDC1所成的二面角而这两的平面为固定的不变的平面所以夹角也为定值，‎ 故②正确；‎ 对于③三棱锥D﹣BPC1的体积还等于三棱锥的体积P﹣DBC1的体积，‎ 而平面DBC1为固定平面且大小一定，又因为P∈AD1，而AD1∥平面BDC1，‎ 所以点A到平面DBC1的距离即为点P到该平面的距离，‎ 所以三棱锥的体积为定值，故③正确．‎ 故选D．‎ ‎　‎ ‎11．下列表格所示的五个散点，原本数据完整，且利用最小二乘法求得这五个散点的线性回归直线方程为=0.8x﹣155，后因某未知原因第5组数据的y值模糊不清，此位置数据记为m（如表所示），则利用回归方程可求得实数m的值为（　　）‎ x ‎196‎ ‎197‎ ‎200‎ ‎203‎ ‎204‎ y ‎1‎ ‎3‎ ‎6‎ ‎7‎ m A．8.3 B．8.2 C．8.1 D．8‎ ‎【考点】线性回归方程．‎ ‎【分析】根据回归直线经过样本数据中心点，求出x、y的平均数，即可求出m值．‎ ‎【解答】解：根据题意，计算=×=200，‎ ‎=×（1+3+6+7+m）=，‎ 代入回归方程=0.8x﹣155中，‎ 可得=0.8×200﹣155=25，‎ 解得m=8．‎ 故选：D．‎ ‎　‎ ‎12．已知三棱柱ABC﹣A1B1C1的侧棱与底面边长都相等，A1在底面ABC上的射影为BC的中点，则异面直线AB与CC1所成的角的余弦值为（　　）‎ A． B． C． D．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】首先找到异面直线AB与CC1所成的角（如∠A1AB）；而欲求其余弦值可考虑余弦定理，则只要表示出A1B的长度即可；不妨设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1，利用勾股定理即可求之．‎ ‎【解答】解：设BC的中点为D，连接A1D、AD、A1B，易知θ=∠A1AB即为异面直线AB与CC1所成的角；‎ 并设三棱柱ABC﹣A1B1C1的侧棱与底面边长为1，‎ 则|AD|=，|A1D|=，|A1B|=，‎ 由余弦定理，得cosθ==．‎ 故选B．‎ ‎　‎ 二、填空题（5×4=20分）‎ ‎13．已知A表示点，a，b，c表示直线，M，N表示平面，给出以下命题：‎ ‎①a⊥M，若M⊥N，则a∥N ‎ ‎②a⊥M，若b∥M，c∥a，则a⊥b，c⊥b ‎③a⊥M，b⊄M，若b∥M，则b⊥a ‎④a⊂β，b∩β=A，c为b在β内的射影，若a⊥c，则a⊥b．‎ 其中命题成立的是　②③④　．‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】根据空间线面之间的位置关系及几何特征，逐一分析四个命题的真假，可得答案．‎ ‎【解答】解：①a⊥M，若M⊥N，则a∥N，或a⊂N，故错误；‎ ‎②a⊥M，若b∥M，c∥a，则a⊥b，c⊥b，故正确；‎ ‎③a⊥M，b⊄M，若b∥M，则b⊥a，故正确；‎ ‎④a⊂β，b∩β=A，c为b在β内的射影，若a⊥c，则a⊥b，故正确．‎ 故答案为：②③④‎ ‎　‎ ‎14．执行如图所示的程序框图，若输入n的值为8，则输出的s的值为　8　．‎ ‎【考点】循环结构．‎ ‎【分析】由已知中的程序框图及已知中输入8，可得：进入循环的条件为i＜8，即i=2，4，6模拟程序的运行结果，即可得到输出的s值．‎ ‎【解答】解：当i=2，k=1时，s=2，；‎ 当i=4，k=2时，s=（2×4）=4；‎ 当i=6，k=3时，s=（4×6）=8；‎ 当i=8，k=4时，不满足条件“i＜8”，退出循环，‎ 则输出的s=8‎ 故答案为：8‎ ‎　‎ ‎15．如图，在正方体ABCD﹣A1B1C1D1中，M、N分别是CD、CC1的中点，则异面直线A1M与DN所成的角的大小是　90°　．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】以D为坐标原点，建立空间直角坐标系，利用向量的方法求出与夹角求出异面直线A1M与DN所成的角．‎ ‎【解答】解：以D为坐标原点，建立如图所示的空间直角坐标系．设棱长为2，‎ 则D（0，0，0），N（0，2，1），M（0，1，0），A1（2，0，2），=（0，2，1），=（﹣2，1，﹣2）‎ ‎•=0，所以⊥，即A1M⊥DN，异面直线A1M与DN所成的角的大小是90°，‎ 故答案为：90°．‎ ‎　‎ ‎16．甲、乙两艘轮船都要停靠在同一个泊位，它们可能在一昼夜的任意时刻到达．甲、乙两船停靠泊位的时间分别为4小时与2小时，则有一艘船停靠泊位时必需等待一段时间的概率为　　．‎ ‎【考点】几何概型．‎ ‎【分析】分析知如两船到达的时间间隔超过了停泊的时间则不需要等待，要求一艘船停靠泊位时必须等待一段时间的概率；即计算一船到达的时间恰好另一船还没有离开，此即是所研究的事件．‎ ‎【解答】解：设甲船在x点到达，乙船在y点到达，必须等待的事件需要满足如下条件：‎ ‎，‎ 画出不等式组表示的平面区域如图所示；‎ 所以p（A）=1﹣=；‎ 所以一艘船停靠泊位时必须等待一段时间的概率是．‎ 故答案为：．‎ ‎　‎ 三、解答题（10+12×5=70分）‎ ‎17．某市规定，高中学生在校期间须参加不少于80小时的社区服务才合格．某校随机抽取20位学生参加社区服务的数据，按时间段[75，80），[80，85），[85，90），[90，95），[95，100]（单位：小时）进行统计，其频率分布直方图如图所示．‎ ‎（Ⅰ）求抽取的20人中，参加社区服务时间不少于90小时的学生人数；‎ ‎（Ⅱ）从参加社区服务时间不少于90小时的学生中任意选取2人，求所选学生的参加社区服务时间在同一时间段内的概率．‎ ‎【考点】古典概型及其概率计算公式．‎ ‎【分析】（I）利用频率分布直方图，求出频率，进而根据频数=频率×样本容量，得到答案；‎ ‎（II）先计算从参加社区服务时间不少于90小时的学生中任意选取2人的情况总数，再计算所选学生的参加社区服务时间在同一时间段内的情况数，代入古典概型概率计算公式，可得答案．‎ ‎【解答】解：（Ⅰ）由题意可知，‎ 参加社区服务在时间段[90，95）的学生人数为20×0.04×5=4（人），‎ 参加社区服务在时间段[95，100]的学生人数为20×0.02×5=2（人）．‎ 所以参加社区服务时间不少于90小时的学生人数为 4+2=6（人）．‎ ‎…‎ ‎（Ⅱ）设所选学生的服务时间在同一时间段内为事件A．‎ 由（Ⅰ）可知，‎ 参加社区服务在时间段[90，95）的学生有4人，记为a，b，c，d；‎ 参加社区服务在时间段[95，100]的学生有2人，记为A，B．‎ 从这6人中任意选取2人有ab，ac，ad，aA，aB，bc，bd，bA，bB，cd，cA，cB，dA，dB，AB 共15种情况．‎ 事件A包括ab，ac，ad，bc，bd，cd，AB共7种情况．‎ 所以所选学生的服务时间在同一时间段内的概率．…‎ ‎　‎ ‎18．已知：四棱锥P﹣ABCD的底面为正方形，PA⊥底面ABCD，E、F分别为AB、PD的中点，PA=a，∠PDA=45°‎ ‎（1）求证：AF∥平面PCE； ‎ ‎（2）求证：平面PCE⊥平面PCD；‎ ‎（3）求点D到平面PCE的距离．‎ ‎【考点】平面与平面垂直的判定；直线与平面平行的判定；点、线、面间的距离计算．‎ ‎【分析】（1）取PC的中点G，连接FG、EG，证出AF∥EG，由线面平行的判定定理，即可证出：AF∥平面PCE．‎ ‎（2）先证出AF⊥平面PCD，再由（1），可证EG⊥平面PCD，由面面垂直的判定定理即可证出平面PCE⊥平面PCD；‎ ‎（3）过点D作DH⊥PC于H，DH的长为点D到平面PEC的距离．‎ ‎【解答】（1）证明：取PC的中点为G，连结FG、EG ‎∵FG∥DC，FG=DC，DC∥AB，AE=AB ‎∴FG∥AE且 FG=A ‎∴四边形AFGE为平行四边形，‎ ‎∴AF∥EG． ‎ 又∵AF⊄平面PCE，EG⊂平面PCE，‎ ‎∴AF∥平面PCE…‎ ‎（2）证明：∵PA⊥平面ABCD，AD⊥D，∴PD⊥DC ‎∴∠PDA为二面角P﹣CD﹣B的平面角，∴∠PDA=45°，即△PAD为等腰直角三角形 又∵F为PD的中点，∴AF⊥PD ①‎ 由DC⊥AD，DC⊥PD，AD∩PD=D，‎ 得：DC⊥平面PAD．‎ 而AF⊂平面PAD，‎ ‎∴AF⊥DC ②‎ 由①②得AF⊥平面PDC．‎ 而EG∥AF ‎∴EG⊥平面PDC，‎ 又EG⊂平面PCE，‎ ‎∴平面PCE⊥平面PDC…‎ ‎（3）解：过点D作DH⊥PC于H．‎ ‎∵平面PCE⊥平面PDC，∴DH⊥平面PEC．‎ 即DH的长为点D到平面PEC的距离．‎ 在Rt△PAD中，PA=AD=a，PD=a 在Rt△PDC中，PD=a，CD=a，‎ PC=a，DH=a．‎ 即：点D到平面PCE的距离为a…‎ ‎　‎ ‎19．某校100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50，60），[60，70），[70，80），[80，90），[90，100]．‎ ‎（1）求图中a的值；‎ ‎（2）根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎（3）若这100名学生语文成绩某些分数段的人数（x）与数学成绩相应分数段的人数（y）之比如表所示，求数学成绩在[50，90）之外的人数．‎ 分数段 ‎[50，60）‎ ‎[60，70）‎ ‎[70，80）‎ ‎[80，90）‎ x：y ‎1：1‎ ‎2：1‎ ‎3：4‎ ‎4：5‎ ‎【考点】用样本的频率分布估计总体分布；频率分布直方图；众数、中位数、平均数．‎ ‎【分析】（1）由频率分布直方图的性质可10（2a+0.02+0.03+0.04）=1，解方程即可得到a的值；‎ ‎（2）由平均数加权公式可得平均数为55×0.05+65×0.4+75×0.3+85×0.2+95×0.05，计算出结果即得；‎ ‎（3）按表中所给的数据分别计算出数学成绩在分数段的人数，从总人数中减去这些段内的人数即可得出数学成绩在[50，90）之外的人数．‎ ‎【解答】解：（1）依题意得，10（2a+0.02+0.03+0.04）=1，解得a=0.005；‎ ‎（2）这100名学生语文成绩的平均分为：55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73（分）；‎ ‎（3）数学成绩在[50，60）的人数为：100×0.05=5，‎ 数学成绩在[60，70）的人数为：，‎ 数学成绩在[70，80）的人数为：，‎ 数学成绩在[80，90）的人数为：，‎ 所以数学成绩在[50，90）之外的人数为：100﹣5﹣20﹣40﹣25=10．‎ ‎　‎ ‎20．已知四棱锥P﹣GBCD中（如图），PG⊥平面GBCD，GD∥BC，GD=BC，且BG⊥GC，GB=GC=2，E是BC的中点，PG=4‎ ‎（Ⅰ）求异面直线GE与PC所成角的余弦值；‎ ‎（Ⅱ）若F点是棱PC上一点，且DF⊥GC，PF：FC=k，求k的值．‎ ‎【考点】异面直线及其所成的角．‎ ‎【分析】（Ⅰ）直接作出异面直线所成角的平面角，通过余弦定理求解．‎ ‎（Ⅱ）由线线垂直转化为线面垂直及面面垂直然后建立比例关系，最后求参数的值．‎ ‎【解答】解：（Ⅰ）在平面ABCD内，过C点作CH∥EG 交AD于H，连结PH，则∠PCH（或其补角）就是异 面直线GE与PC所成的角．‎ 在△PCH中，‎ 由余弦定理得，cos∠PCH=‎ ‎∴异面直线GE与PC所成角的余弦值为．‎ ‎（Ⅱ）在平面GBCD内，过D作DM⊥GC，M为垂足，连结MF，又因为DF⊥GC ‎∴GC⊥平面MFD，‎ ‎∴GC⊥FM 由平面PGC⊥平面GBCD，‎ ‎∴FM⊥平面GBCD∴FM∥PG 由得GM⊥MD，‎ ‎∴GM=GD•cos45°=‎ ‎∵，‎ ‎∴k=3‎ ‎　‎ ‎21．等边三角形ABC的边长为2沿平行于BC的线段PQ折起，使平面APQ⊥平面PBCQ，设点A到直线PQ的距离为x，AB的长为d．‎ ‎（Ⅰ）x为何值时，d2取得最小值，最小值是多少；‎ ‎（Ⅱ）若∠BAC=θ，求cosθ的最小值．‎ ‎【考点】直线与平面垂直的判定；余弦定理．‎ ‎【分析】（I）如图（1）为折叠前对照图，图（2）为折叠后的空间图形．利用面面垂直和线面垂直的判定与性质定理和二次函数的单调性即可得出；‎ ‎（II）在等腰△ADC中，使用余弦定理和利用余弦函数的单调性即可得出．‎ ‎【解答】解：（Ⅰ）如图（1）为折叠前对照图，图（2）为折叠后的空间图形．‎ ‎∵平面APQ⊥平面PBCQ，又∵AR⊥PQ，‎ ‎∴AR⊥平面PBCQ，∴AR⊥RB．‎ 在Rt△BRD中，BR2=BD2+RD2=，‎ AR2=x2．‎ 故d2=BR2+AR2=．‎ ‎∴当时，d2取得最小值．‎ ‎（Ⅱ）∵AB=AC=d，BC=2，‎ ‎∴在等腰△ADC中，由余弦定理得，即，‎ ‎∴当时，cosθ取得最小值．‎ ‎　‎ ‎22．如图，在三棱锥D﹣ABC中，已知△BCD是正三角形，AB⊥平面BCD，AB=BC=a，E为BC的中点，F在棱AC上，且AF=3FC．‎ ‎（1）求三棱锥D﹣ABC的表面积；‎ ‎（2）求证AC⊥平面DEF；‎ ‎（3）若M为BD的中点，问AC上是否存在一点N，使MN∥平面DEF？若存在，说明点N的位置；若不存在，试说明理由．‎ ‎【考点】棱锥的结构特征．‎ ‎【分析】（1）分别作出三角形的高，求出四个三角形的面积，然后求三棱锥D﹣ABC的表面积；‎ ‎（2）要证AC⊥平面DEF，先证AC⊥DE，再证AC⊥EF，即可．‎ ‎（3）M为BD的中点，连CM，设CM∩DE=O，连OF，只要MN∥OF即可，求出CN．‎ ‎【解答】解：（1）∵AB⊥平面BCD，∴AB⊥BC，AB⊥BD．‎ ‎∵△BCD是正三角形，且AB=BC=a，∴AD=AC=．‎ 设G为CD的中点，则CG=，AG=．‎ ‎∴，，．‎ 三棱锥D﹣ABC的表面积为．‎ ‎（2）取AC的中点H，∵AB=BC，∴BH⊥AC．‎ ‎∵AF=3FC，∴F为CH的中点．‎ ‎∵E为BC的中点，∴EF∥BH．则EF⊥AC．‎ ‎∵△BCD是正三角形，∴DE⊥BC．‎ ‎∵AB⊥平面BCD，∴AB⊥DE．‎ ‎∵AB∩BC=B，∴DE⊥平面ABC．∴DE⊥AC．‎ ‎∵DE∩EF=E，∴AC⊥平面DEF．‎ ‎（3）存在这样的点N，‎ 当CN=时，MN∥平面DEF．‎ 连CM，设CM∩DE=O，连OF．‎ 由条件知，O为△BCD的重心，CO=CM．‎ ‎∴当CF=CN时，MN∥OF．∴CN=．‎ ‎　‎ ‎2016年11月26日