2018届二轮复习（文）专题五立体几何 27页

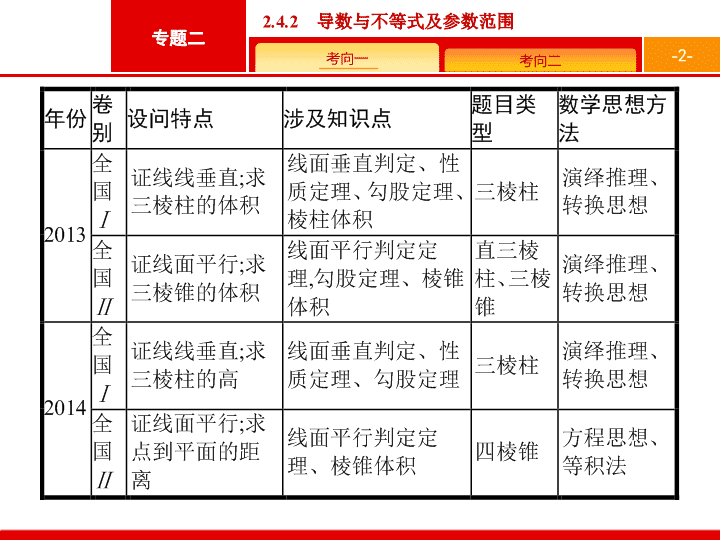
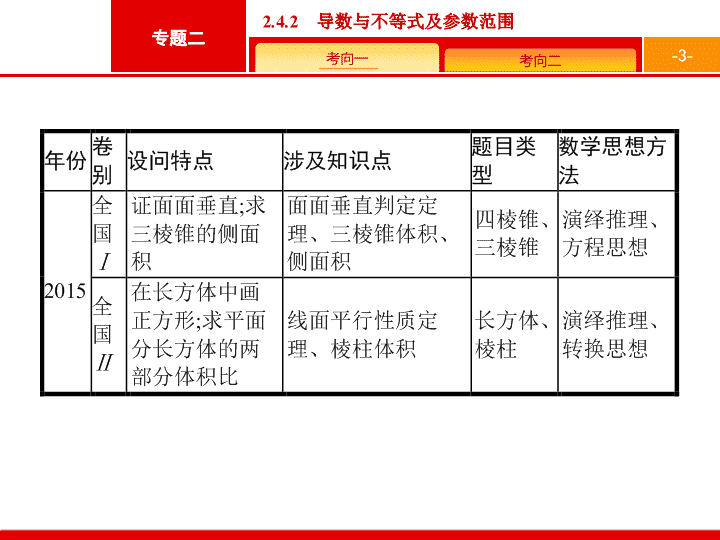
5.3 　立体几何大题 - 2 - - 3 - - 4 - - 5 - - 6 - 1 . 证明线线平行和线线垂直的常用方法 (1) 证明线线平行常用的方法 : ① 利用平行公理 , 即证两直线同时和第三条直线平行 ; ② 利用平行四边形进行平行转换 ; ③ 利用三角形的中位线定理证线线平行 ; ④ 利用线面平行、面面平行的性质定理进行平行转换 . (2) 证明线线垂直常用的方法 : ① 利用等腰三角形底边上的中线即高线的性质 ; ② 勾股定理 ; ③ 线面垂直的性质 : 即要证两直线垂直 , 只需证明一直线垂直于另一直线所在的平面即可 , 即 l ⊥ α , a ⊂ α ⇒ l ⊥ a. 2 . 垂直、平行关系证明中应用转化与化归思想的常见类型 (1) 证明线面、面面平行 , 需转化为证明线线平行 . (2) 证明线面垂直 , 需转化为证明线线垂直 . (3) 证明线线垂直 , 需转化为证明线面垂直 . (4) 证明面面垂直 , 需转化为证明线面垂直 , 进而转化为证明线线垂直 . - 7 - 3 . 求几何体的表面积或体积 (1) 对于规则几何体 , 可直接利用公式计算 . 对于某些三棱锥 , 有时可采用等体积转换法求解 . (2) 对于不规则几何体 , 可采用割补法求解 . (3) 求解旋转体的表面积和体积时 , 注意圆柱的轴截面是矩形 , 圆锥的轴截面是等腰三角形 , 圆台的轴截面是等腰梯形的应用 . 4 . 解决平面图形的翻折问题 , 关键是抓住平面图形翻折前后的不变性 , 即两条直线的平行与垂直关系以及相关线段的长度、角度等的不变性 . 5 . 3 . 1 　 空间中的平行与 几何 体 的体积 - 9 - 考向一 考向二 考向 三 平行关系的证明及求体积 例 1 如 图 , 四棱锥 P-ABCD 中 , PA ⊥ 底面 ABCD , AD ∥ BC , AB=AD=AC= 3, PA=BC= 4, M 为线段 AD 上一点 , AM= 2 MD , N 为 PC 的中点 . ( 1) 证明 MN ∥ 平面 PAB ; (2) 求四面体 N-BCM 的体积 . - 10 - 考向一 考向二 考向 三 取 BP 的中点 T , 连接 AT , TN , 由 N 为 PC 中点知 TN ∥ BC , 又 AD ∥ BC , 故 TN