高中数学（人教A版）必修4第2章 平面向量 测试题（含详解） 9页

第二章测试 ‎ (时间：120分钟，满分：150分)‎ 一、选择题(本大题共12小题，每题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1．有下列四个表达式：‎ ‎①|a＋b|＝|a|＋|b|；‎ ‎②|a－b|＝±(|a|－|b|)；‎ ‎③a2>|a|2；‎ ‎④|a·b|＝|a|·|b|.‎ 其中正确的个数为(　　)‎ A．0　　　　B．‎2　‎　　　C．3　　　　D．4‎ 解析　对于①仅当a与b同向时成立．对于②左边|a－b|≥0，而右边可能≤0，∴不成立．对于③∵a2＝|a|2，∴a2>|a|2不成立．对于④当a⊥b时不成立，综上知，四个式子都是错误的．‎ 答案　A ‎2．下列命题中，正确的是(　　)‎ A．a＝(－2,5)与b＝(4，－10)方向相同 B．a＝(4,10)与b＝(－2，－5)方向相反 C．a＝(－3,1)与b＝(－2，－5)方向相反 D．a＝(2,4)与b＝(－3,1)的夹角为锐角 解析　在B中，a＝(4,10)＝－2(－2，－5)＝－2b，‎ ‎∴a与b方向相反．‎ 答案　B ‎3．已知A，B是圆心为C，半径为的圆上两点，且||＝，则·等于(　　)‎ A．－ B. ‎ C．0 D. 解析　易知△ABC为正三角形，·＝·cos120°＝－，应选A.‎ 答案　A ‎4．已知向量a＝，b＝(x＋1,2)，其中x>0，若a∥b，则x的值为(　　)‎ A．8 B．4 ‎ C．2 D．0‎ 解析　∵a∥b，∴(8＋x)×2－x(x＋1)＝0，即x2＝16，又x>0，∴x＝4.‎ 答案　B ‎5．在△ABC中，M是BC的中点，AM＝1，点P在AM上且满足＝2，则·(＋)等于(　　)‎ A. B. ‎ C．－ D．－ 解析　M为BC的中点，得＋＝2＝，‎ ‎∴·(＋)＝2.‎ 又∵＝2，∴||＝||＝.‎ ‎∴2＝||2＝.‎ 答案　A ‎6．若向量a＝(1,1)，b＝(2,5)，c＝(3，x)，满足条件(‎8a－b)·c＝30，则x＝(　　)‎ A．6 B．5 ‎ C．4 D．3‎ 解析　‎8a－b＝8(1,1)－(2,5)＝(6,3)，c＝(3，x)，‎ ‎∴(‎8a－b)·c＝(6,3)·(3，x)＝18＋3x.‎ 又(‎8a－b)·c＝30，∴18＋3x＝30，x＝4.‎ 答案　C ‎7．向量a＝(－1,1)，且a与a＋2b方向相同，则a·b的取值范围是(　　)‎ A．(－1,1) B．(－1，＋∞)‎ C．(1，＋∞) D．(－∞，1)‎ 解析　依题意可设a＋2b＝λa(λ>0)，‎ 则b＝(λ－1)a，‎ ‎∴a·b＝(λ－1)a2＝(λ－1)×2＝λ－1>－1.‎ 答案　B ‎8．设单位向量e1，e2的夹角为60°，则向量3e1＋4e2与向量e1的夹角的余弦值为(　　)‎ A. B. C. D. 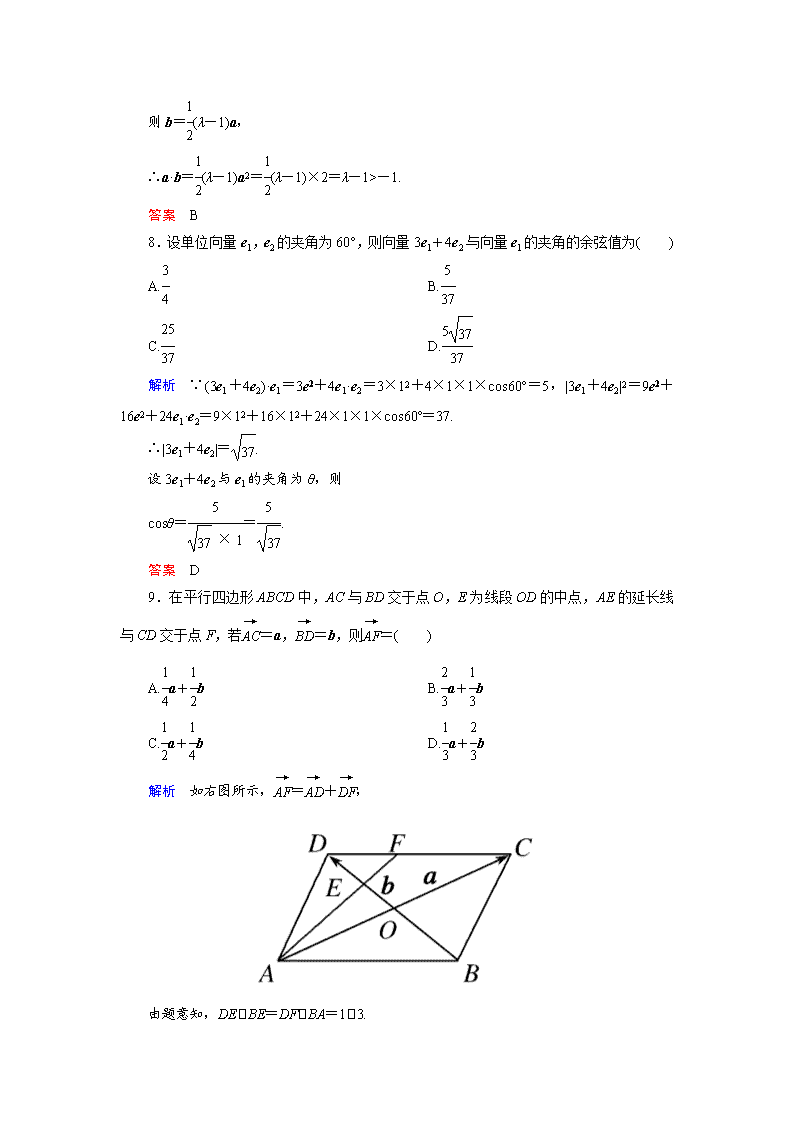解析　∵(3e1＋4e2)·e1＝3e＋4e1·e2＝3×12＋4×1×1×cos60°＝5，|3e1＋4e2|2＝9e＋16e＋24e1·e2＝9×12＋16×12＋24×1×1×cos60°＝37.‎ ‎∴|3e1＋4e2|＝.‎ 设3e1＋4e2与e1的夹角为θ，则 cosθ＝＝.‎ 答案　D ‎9．在平行四边形ABCD中，AC与BD交于点O，E为线段OD的中点，AE的延长线与CD交于点F，若＝a，＝b，则＝(　　)‎ A.a＋b B.a＋b C.a＋b D.a＋b 解析　如右图所示，＝＋，‎ 由题意知，DEBE＝DFBA＝13.‎ ‎∴＝.‎ ‎∴＝a＋b＋(a－b)＝a＋b.‎ 答案　B ‎10．已知点B为线段AC的中点，且A点坐标为(－3,1)，B点坐标为，则C点坐标为(　　)‎ A．(1，－3) B. C．(4,2) D．(－2,4)‎ 解析　设C(x，y)，则由＝，得 ＝，‎ ‎∴⇒∴C(4,2)．‎ 答案　C ‎11．已知向量＝(2,2)，＝(4,1)，在x轴上求一点P，使·有最小值，则点P的坐标为(　　)‎ A．(－3,0) B．(2,0)‎ C．(3,0) D．(4,0)‎ 解析　设＝(x,0)，则＝(x－2，－2)，＝(x－4，－1)，∴·＝(x－2)(x－4)－2×(－1)＝x2－6x＋10＝(x－3)2＋1，∴当x＝3时，·有最小值1，此时P(3,0)．‎ 答案　C ‎12．下列命题中正确的个数是(　　)‎ ‎①若a与b为非零向量，且a∥b，则a＋b必与a或b的方向相同；‎ ‎②若e为单位向量，且a∥e，则a＝|a|e；‎ ‎③a·a·a＝|a|3；‎ ‎④若a与b共线，又b与c共线，则a与c必共线；‎ ‎⑤若平面内有四点A，B，C，D，则必有＋＝＋.‎ A．1 B．2‎ C．3 D．4‎ 解析　易知①②③④均错误，⑤正确，因为＋＝＋，∴－＝－，即＝，∴⑤正确．‎ 答案　A 二、填空题(本大题共4小题，每题5分，共20分．将答案填在题中横线上)‎ ‎13．已知a＝(2cosθ，2sinθ)，b＝(3，)，且a与b共线，θ∈[0,2π)，则θ＝________.‎ 解析　由a∥b，得2cosθ＝6sinθ，∵cosθ≠0，∴tanθ＝，又θ∈[0,2π)，∴θ＝或 ‎.‎ 答案　或π ‎14．假设|a|＝2，b＝(－1,3)，若a⊥b，则a＝________.‎ 解析　设a＝(x，y)，则有x2＋y2＝20.①‎ 又a⊥b，∴a·b＝0，∴－x＋3y＝0.②‎ 由①②解得x＝3，y＝，或x＝－3，y＝－，‎ ‎∴a＝(3，)，或a＝(－3，－)．‎ 答案　(3，)或(－3，－)‎ ‎15．已知a＋b＝2i－8j，a－b＝－8i＋16j，那么a·b＝________.(其中i，j为夹角90°的单位向量)‎ 解析　由得 ‎∴a＝(－3,4)，b＝(5，－12)．‎ ‎∴a·b＝－3×5＋4×(－12)＝－63.‎ 答案　－63‎ ‎16．若等边△ABC的边长为2，平面内一点M满足＝＋，则·＝________.‎ 解析　∵等边△ABC的边长为2，‎ ‎∴如下图建立直角坐标系．‎ ‎∴＝(，－3)，＝(－，－3)．‎ ‎∴＝＋＝.‎ ‎∴＝＋ ‎＝(0,3)＋＝.‎ ‎∴·＝· ‎＝－＋＝－2.‎ 答案　－2‎ 三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤)‎ ‎17．(10分)已知|a|＝3，|b|＝2，a与b的夹角为60°，c＝‎3a＋5b，d＝ma－3b.‎ ‎(1)当m为何值时，c与d垂直？‎ ‎(2)当m为何值时，c与d共线？‎ 解　(1)令c·d＝0，则(‎3a＋5b)·(ma－3b)＝0，‎ 即‎3m|a|2－15|b|2＋(‎5m－9)a·b＝0，‎ 解得m＝.‎ 故当m＝时，c⊥d.‎ ‎(2)令c＝λd，则‎3a＋5b＝λ(ma－3b)‎ 即(3－λm)a＋(5＋3λ)b＝0，‎ ‎∵a，b不共线，‎ ‎∴解得 故当m＝－时，c与d共线．‎ ‎18．(12分)如图所示，在△ABC中，∠C为直角，CA＝CB，D是CB的中点，E是AB上的点，且AE＝2EB，求证：AD⊥CE.‎ 证明　设此等腰直角三角形的直角边长为a，则 ·＝(＋)·(＋)‎ ‎＝·＋·＋·＋· ‎＝－a2＋0＋a·a·＋·a· ‎＝－a2＋a2＋a2＝0，‎ ‎∴⊥，∴AD⊥CE.‎ ‎19．(12分)已知在△ABC中，A(2，－1)，B(3,2)，C(－3，－1)，AD为BC边上的高，求||与点D的坐标．‎ 解　设D点坐标为(x，y)，则＝(x－2，y＋1)，‎ ＝(－6，－3)，＝(x－3，y－2)，‎ ‎∵D在直线BC上，即与共线，‎ ‎∴存在实数λ，使＝λ，‎ 即(x－3，y－2)＝λ(－6，－3)．‎ ‎∴∴x－3＝2(y－2)，‎ 即x－2y＋1＝0.①‎ 又∵AD⊥BC，∴·＝0，‎ 即(x－2，y＋1)·(－6，－3)＝0.‎ ‎∴－6(x－2)－3(y＋1)＝0.②‎ 由①②可得 ‎∴||＝ ＝，‎ 即||＝，D(1,1)．‎ ‎20．(12分)在直角坐标系中，已知＝(4，－4)，＝(5,1)，在方向上的射影数量为||，求的坐标．‎ 解　设点M的坐标为M(x，y)．‎ ‎∵在方向上的射影数量为||，‎ ‎∴⊥，∴·＝0.‎ 又＝(x，y)，＝(5－x,1－y)，‎ ‎∴x(5－x)＋y(1－y)＝0.‎ 又点O，M，A三点共线，∴∥.‎ ‎∴＝.‎ ‎∴解得 ‎∴＝－＝(5－2,1＋2)＝(3,3)．‎ ‎21．(12分)在四边形ABCD中，＝a，＝b，＝c，＝d，且a·b＝b·c＝c·d＝d·a，判断四边形的形状．‎ 解　∵a＋b＋c＋d＝0，‎ ‎∴(a＋b)2＝(c＋d)2，‎ ‎∴a2＋‎2a·b＋b2＝c2＋‎2c·d＋d2.‎ ‎∵a·b＝c·d，‎ ‎∴a2＋b2＝c2＋d2.①‎ 同理a2＋d2＝b2＋c2.②‎ ‎①②两式相减，得b2－d2＝d2－b2，‎ ‎①②两式相加，得a2＝c2，‎ ‎∴|b|＝|d|，|a|＝|c|.‎ ‎∴四边形ABCD是平行四边形．‎ 又a·b＝b·c，‎ ‎∴b·(a－c)＝0.‎ ‎∴b·‎2a＝0，即a·b＝0.‎ ‎∴a⊥b，即AB⊥BC.‎ ‎∴四边形ABCD是矩形．‎ ‎22．(12分)已知三个点A(2,1)，B(3,2)，D(－1,4)．‎ ‎(1)求证：⊥；‎ ‎(2)要使四边形ABCD为矩形，求点C的坐标，并求矩形ABCD两对角线所夹锐角的余弦值．‎ 解　(1)证明：A(2,1)，B(3,2)，D(－1,4)．‎ ‎∴＝(1,1)，＝(－3,3)．‎ 又∵·＝1×(－3)＋1×3＝0，∴⊥.‎ ‎(2)∵⊥，若四边形ABCD为矩形，‎ 则＝.‎ 设C点的坐标为(x，y)，则有 ‎(1,1)＝(x＋1，y－4)，‎ ‎∴∴ ‎∴点C的坐标为(0,5)．‎ 由于＝(－2,4)，＝(－4,2)，‎ ‎∴·＝(－2)×(－4)＋4×2＝16，||＝2，|＝2.‎ 设对角线AC与BD的夹角为θ，‎ 则cosθ＝＝＝>0.‎ 故矩形ABCD两条对角线所夹锐角的余弦值为.‎