数学（理）卷·2017届福建省莆田市二十五中高三12月月考（2016 9页

莆田第二十五中学2016—2017学年上学期月考试卷 高三 数学(理)‎ 一、选择题（本大题共10小题，每小题5分，共60分 ‎ ‎1已知集合，则( )‎ ‎ A． B． C． D．‎ ‎2.已知是实数，则“”是“”的 ‎ A.充分而不必要条件 B.必要而不充分条件 ‎ ‎ C.充要条件 D.既不充分也不必要条件 ‎3若变量x，y满足约束条件，则z=2x+y的最大值等于（　　）‎ A．7 B．‎8 ‎C．11 D．10‎ ‎4.若命题“,使得”为假命题，则实数的取值范围是 ‎ A. B. C. D.‎ ‎5已知数列﹛an﹜为等比数列，且，则的值为 ‎ A． B． C． D． ‎ ‎6．如图给出的是计算的值的一个程序框图，其中菱形判断框内应填入的条件是（　　）‎ A．i＞8 B．i＞‎9 ‎C．i＞10 D．i＞11‎ ‎7. 函数的零点个数是（ ）‎ A．1 B．3 C．2 D．4 ‎ ‎8. 若，则 ‎ A. B. C. D.‎ ‎9.设错误！未找到引用源。是单位向量，且错误！未找到引用源。，则错误！未找到引用源。‎ 的最小值为（ ）‎ ‎ A．-2 B．错误！未找到引用源。 C.-1 D．错误！未找到引用源。‎ ‎10.若，则 ‎ A. B. C. D.‎ ‎11.已知函数，则关于的不等式的解集是 ‎ A. B. C. D.‎ ‎12.已知函数,若对恒成立,则实数的取值范围是 ‎ A. B. C. D.‎ 第Ⅱ卷（主观题90分）‎ 二、填空题（本大题共4小题，每小题5分，共20分）‎ ‎13.已知a,b∈R,i为虚数单位,若i(1+ai)=1+bi,则a+b=　　　　.‎ ‎14．设是第二象限角，P(x,4)为其终边上的一点，且cos＝x，则tan＝_____‎ ‎15.等比数列错误！未找到引用源。中，错误！未找到引用源。，错误！未找到引用源。，则数列错误！未找到引用源。的前8项和等于----------- ‎ ‎16.已知是定义在上且周期为的函数，在区间上，‎ ‎，其中，若，则 .‎ 三、解答题：解答应写出文字说明、演算步骤或证明过程. 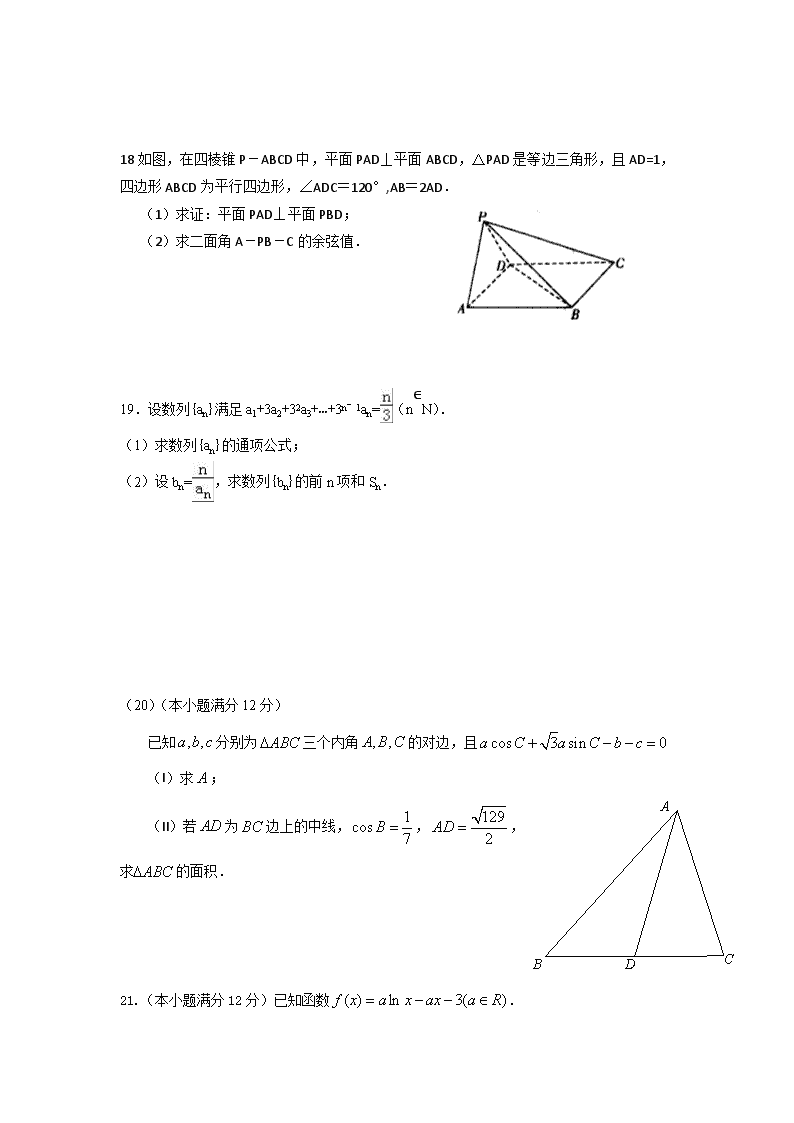‎ ‎17..(本小题满分12分)已知函数，求：（1）函数f(x)的最小正周期；（2）函数f(x)的单调递增区间.‎ ‎18如图，在四棱锥P－ABCD中，平面PAD⊥平面ABCD，△PAD是等边三角形，且AD=1，四边形ABCD为平行四边形，∠ADC＝120°,AB＝2AD． ‎ ‎（1）求证：平面PAD⊥平面PBD； ‎ （2） 求二面角A－PB－C的余弦值．‎ ‎19．设数列{an}满足a1+‎3a2+‎32a3+…+3n﹣1an=（n∈N）．‎ ‎（1）求数列{an}的通项公式；‎ ‎（2）设bn=，求数列{bn}的前n项和Sn．‎ ‎ ‎ ‎（20）（本小题满分12分）‎ 已知分别为三个内角的对边，且 ‎（I）求；‎ A B C D ‎（II）若为边上的中线，，，求的面积．‎ ‎21.（本小题满分12分）已知函数.‎ ‎（Ⅰ）求函数的单调区间；‎ ‎（Ⅱ）若函数的图象在点处的切线的倾斜角为，对于任意的，函数在区间上总不是单调函数，求的取值范围；‎ ‎（Ⅲ）求证：.‎ ‎ ‎ ‎ 22．（本小题满分10分）选修4-4：坐标系与参数方程选讲 已知极坐标系的极点与直角坐标系的原点重合，极轴与直角坐标系中轴的正半轴重合．若曲线的参数方程为为参数），直线的极坐标方程为．‎ ‎ (1)将曲线的参数方程化为极坐标方程；‎ ‎(2)由直线上一点向曲线引切线，求切线长的最小值．‎ ‎ ‎ 数学(理)试卷参考答案及评分标准 ‎ A B D C A C B D D C A C ‎ ‎13. 0 14.－ 15.4 16.‎ ‎17解：（1）‎ ‎ ‎ ‎ …………4分 ‎ ∴最小正周期T= …………6分 ‎ （2）由题意，解不等式………8分 得 ‎ 的单调递增区间是 ………12分 ‎18.(1)证明： 在平行四边形中,,则 ‎，……1分 在中,，所以.……2分 ‎ 又平面平面，所以平面.……3分 又BD平面，所以平面平面. ……4分 ‎(2)由（1）得，以为空间直角原点，‎ 建立空间直角坐标系， ……5分 如图所示，‎ ‎,……6分 设平面的法向量为，则 ‎ 得令，得，‎ 所以平面的法向量为 ； ……8分 ‎ 设平面的法向量为，‎ ‎ 即令，得，‎ 所以平面的法向量为. ……10分 ‎ 所以，……11分 ‎ 所以所求二面角的余弦值为. ……12分 ‎19【考点】数列的求和；数列递推式．‎ ‎【分析】（1）由a1+‎3a2+‎32a3+…+3n﹣1an=⇒当n≥2时，a1+‎3a2+‎32a3+…+3n﹣2an﹣1=，两式作差求出数列{an}的通项．‎ ‎（2）由（1）的结论可知数列{bn}的通项．再用错位相减法求和即可．‎ ‎【解答】解：（1）∵a1+‎3a2+‎32a3+…+3n﹣1an=，①‎ ‎∴当n≥2时，a1+‎3a2+‎32a3+…+3n﹣2an﹣1=．②‎ ‎①﹣②，得3n﹣1an=，‎ 所以（n≥2），‎ 在①中，令n=1，得也满足上式．‎ ‎∴．‎ ‎（2）∵，‎ ‎∴bn=n•3n．‎ ‎∴Sn=3+2×32+3×33+…+n•3n．③‎ ‎∴3Sn=32+2×33+3×34+…+n•3n+1．④‎ ‎④﹣③，得2Sn=n•3n+1﹣（3+32+33+…+3n），‎ 即2Sn=n•3n+1﹣．‎ ‎∴．‎ ‎20．命题依据：三解形中的恒等变换，正、余弦定理．‎ ‎【分析】（I）利用正弦定理将边的关系化为角的关系，利用三角恒等变换求出值．‎ ‎（II）先根据两角和差的正弦公式求出，再根据正弦定理得到边长的比值关系，再在或利用余弦定理可求的值，再由三角形面积公式可求结果．‎ ‎【解答】（I）因为 ，由正弦定理得：‎ ‎，即 ‎，……3分 化简得：，所以．……5分 在中，，所以，得．……6分 ‎（II）在中，，得．……7分 则．……8分 由正弦定理得．……9分 设，，在中，由余弦定理得：‎ ‎，则 ‎，解得，‎ 即，……11分 故．……12分 ‎（21）解：（Ⅰ）由（）， …………………………………1分 ‎①当时，显然时，；当时，，‎ 所以此时的单调增区间为，减区间为；‎ ‎②当时， 的单调增区间为，减区间为；‎ ‎③当时，不是单调函数． …………………………………4分 ‎（Ⅱ）由题知，得，‎ 所以， ……………………………5分 所以（），‎ ‎． …………………………………………6分 ‎∵，∴一定有两个不等的实根，‎ 又∵．‎ 不妨设，由已知时，时，‎ 即在上递减，在上递增，依题意知，‎ 于是只需，得．……………………………8分 ‎（Ⅲ）由（Ⅰ）知当时，在上递增，‎ ‎∴，…………………9分 在上式中分别令 得，………………………10分 以上不等式相乘 得，…………………11分 两边同除以 得（），即证……………………12分 ‎22【解析】（1）圆的直角坐标方程为．‎ ‎∵，‎ ‎∴圆的极坐标方程为．‎ ‎(2) ∵直线的极坐标方程为，‎ ‎∴，∴直线的直角坐标方程为．‎ 设直线上点，切点为，圆心，‎ ‎ 则有，‎ ‎ 当最小时，有最小．‎ ‎∵，‎ ‎∴，‎ ‎∴切线长的最小值为．‎