2019届二轮复习等差、等比数列的综合问题课件（26张）（全国通用） 26页

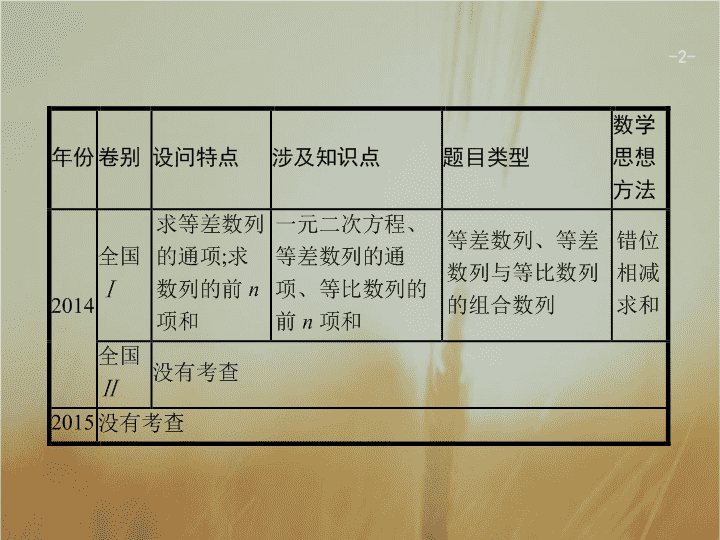
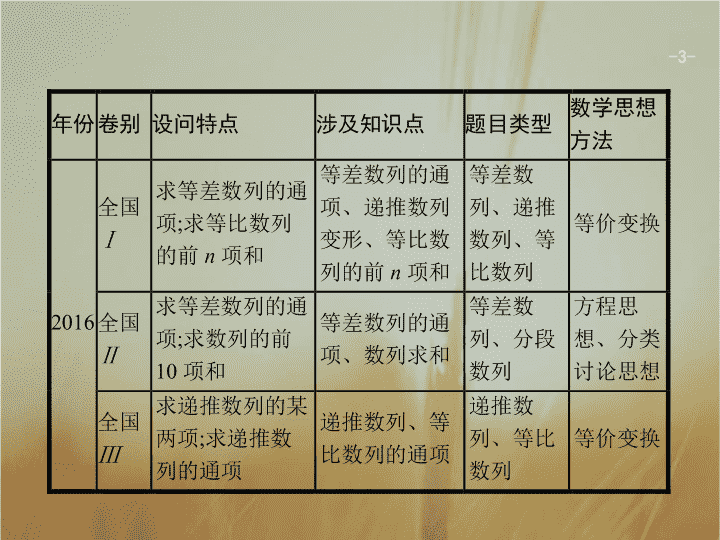
　数列大题 - 2 - - 3 - - 4 - - 5 - - 6 - 1 . 由递推关系式求数列的通项公式 (1)形如 a n+ 1 =a n +f ( n ),利用累加法求通项 . (2)形如 a n+ 1 =a n f ( n ),利用累乘法求通项 . (3)形如 a n+ 1 =pa n +q ,等式两边同时加 转化为等比数列求通项 . - 7 - 2 . 数列求和的常用方法 (1)公式法:利用等差数列、等比数列的求和公式 . (2)错位相减法:适合求数列{ a n · b n }的前 n 项和 S n ,其中{ a n },{ b n }一个是等差数列,另一个是等比数列 . (3)裂项相消法:即将数列的通项分成两个式子的代数和,通过累加抵消中间若干项的方法 . (4)拆项分组法:先把数列的每一项拆成两项(或多项),再重新组合成两个(或多个)简单的数列,最后分别求和 . (5)并项求和法:把数列的两项(或多项)组合在一起,重新构成一个数列再求和,适用于正负相间排列的数列求和 . 4.2.1 　等差、等比数列的综合问题 - 9 - 考向一 考向二 考向三 考向四 考向五 等差 ( 比 ) 数列的判断与证明 例 1 已知数列{ a n }满足 a n+ 1 = 2 a n +n- 1,且 a 1 = 1 . (1)求证:数列{ a n +n }为等比数列; (2)求数列{ a n }的前 n 项和 S n . - 10 - 考向一 考向二 考向三 考向四 考向五 解题心得1 . 判断和证明数列是等差 ( 比 ) 数列的三种方法 . (1) 定义法 : 对于 n ≥ 1 的任意自然数 , 验证 a n+ 1 -a n 为同一常数 . (2) 通项公式法 : 若 a n =kn+b ( n ∈ N * ), 则 { a n } 为等差数列 ; 若 a n =pq kn+b ( n ∈ N * ), 则 { a n } 为等比数列 . (3) 中项公式法 : 若 2 a n =a n- 1 +a n+ 1 ( n ∈ N * , n ≥ 2), 则 { a n } 为等差数列 ; 若 =a n- 1 · a n+ 1 ( n ∈ N * , n ≥ 2), 则 { a n } 为等比数列 . 2 . 对已知数列 a n 与 S n 的关系 , 证明 { a n } 为等差或等比数列的问题 , 解题思路是 : 由 a n 与 S n 的关系递推出 n+ 1 时的关系式 , 两个关系式相减后 , 进行化简、整理 , 最终化归为用定义法证明 . - 11 - 考向一 考向二 考向三 考向四 考向五 对点训练 1 设 S n 为等比数列{ a n }的前 n 项和,已知 S 2 = 2, S 3 =- 6 . (1)求{ a n }的通项公式; (2)求 S n ,并判断 S n+ 1 , S n , S n+ 2 是否成等差数列 . - 12 - 考向一 考向二 考向三 考向四 考向五 等差数列的通项及求和 例 2 (2018 北京卷 , 文 15)设{ a n }是等差数列,且 a 1 = ln 2, a 2 +a 3 = 5ln 2 . (1)求{ a n }的通项公式; - 13 - 考向一 考向二 考向三 考向四 考向五 解 : (1) 设等差数列 { a n } 的公差为 d , ∵ a 2 +a 3 = 5ln 2 . ∴ 2 a 1 + 3 d= 5ln 2, 又 a 1 = ln 2, ∴ d= ln 2 . ∴ a n =a 1 + ( n- 1) d=n ln 2 . (2) 由 (1) 知 a n =n ln 2 . - 14 - 考向一 考向二 考向三 考向四 考向五 解题心得 已知等差数列前几项或者前几项的关系 , 求其通项及前 n 项和时 , 只需利用等差数列的通项公式及求和公式得到几个方程求解即可 . - 15 - 考向一 考向二 考向三 考向四 考向五 对点训练 2 (2018 全国卷 2, 文 17)记 S n 为等差数列{ a n }的前 n 项和,已知 a 1 =- 7, S 3 =- 15 . (1)求{ a n }的通项公式; (2)求 S n ,并求 S n 的最小值 .   解 : (1) 设 { a n } 的公差为 d , 由题意得 3 a 1 + 3 d=- 15 . 由 a 1 =- 7 得 d= 2 . 所以 { a n } 的通项公式为 a n = 2 n- 9 . (2) 由 (1) 得 S n =n 2 - 8 n= ( n- 4) 2 - 16 . 所以当 n= 4 时 , S n 取得最小值 , 最小值为 - 16 . - 16 - 考向一 考向二 考向三 考向四 考向五 等比数列的通项及求和 例 3 (2018 全国卷 3, 文 17)等比数列{ a n }中, a 1 = 1, a 5 = 4 a 3 . (1)求{ a n }的通项公式; (2)记 S n 为{ a n }的前 n 项和,若 S m = 63,求 m. 解 : (1) 设 { a n } 的公比为 q , 由题设得 a n =q n- 1 . 由已知得 q 4 = 4 q 2 , 解得 q= 0( 舍去 ), q=- 2 或 q= 2 . 故 a n = ( - 2) n- 1 或 a n = 2 n- 1 . (2) 若 a n = ( - 2) n- 1 , 则 . 由 S m = 63 得 ( - 2) m =- 188, 此方程没有正整数解 . 若 a n = 2 n- 1 , 则 S n = 2 n - 1 . 由 S m = 63 得 2 m = 64, 解得 m= 6 . 综上 , m= 6 . - 17 - 考向一 考向二 考向三 考向四 考向五 解题心得 已知等比数列前几项或者前几项的关系 , 求其通项及前 n 项和时 , 只需利用等比数列的通项公式及求和公式得到几个方程求解即可 . - 18 - 考向一 考向二 考向三 考向四 考向五 对点训练 3 (2018 北京朝阳期末 , 文 15)已知由实数构成的等比数列{ a n }满足 a 1 = 2, a 1 +a 3 +a 5 = 42 . (1)求数列{ a n }的通项公式; (2)求 a 2 +a 4 +a 6 + … +a 2 n . - 19 - 考向一 考向二 考向三 考向四 考向五 等差、等比数列的综合问题 例 4 (2018 北京海淀模拟 , 文 15)已知等差数列{ a n }的前 n 项和 S n ,且 a 2 = 5, S 3 =a 7 . (1)数列{ a n }的通项公式; (2)若 b n = ,求数列{ a n +b n }前 n 项和 . - 20 - 考向一 考向二 考向三 考向四 考向五 - 21 - 考向一 考向二 考向三 考向四 考向五 解题心得 对于等差、等比数列的综合问题 , 解决的思路主要是方程的思想 , 即运用等差、等比数列的通项公式和前 n 项和公式将已知条件转化成方程或方程组 , 求出首项、公差、公比等基本量 , 再由基本量求出题目要求的量 . - 22 - 考向一 考向二 考向三 考向四 考向五 对点训练 4 已知等差数列{ a n }的前 n 项和为 S n ,等比数列{ b n }的前 n 项和为 T n , a 1 =- 1, b 1 = 1, a 2 +b 2 = 2 . (1)若 a 3 +b 3 = 5,求{ b n }的通项公式; (2)若 T 3 = 21,求 S 3 . 解 (1) 设 { a n } 的公差为 d ,{ b n } 的公比为 q , 则 a n =- 1 + ( n- 1) d , b n =q n- 1 . 由 a 2 +b 2 = 2 得 d+q= 3 . ① 由 a 3 +b 3 = 5, 得 2 d+q 2 = 6 . ② 因此 { b n } 的通项公式为 b n = 2 n- 1 . (2) 由 b 1 = 1, T 3 = 21 得 q 2 +q- 20 = 0, 解得 q=- 5 或 q= 4 . 当 q=- 5 时 , 由 ① 得 d= 8, 则 S 3 = 21 . 当 q= 4 时 , 由 ① 得 d=- 1, 则 S 3 =- 6 . - 23 - 考向一 考向二 考向三 考向四 考向五 可转化为等差、等比数列的问题 例 5 (2018 全国卷 1, 文 17) 已知数列 { a n } 满足 a 1 = 1, na n+ 1 = 2( n+ 1) a n . 设 (1) 求 b 1 , b 2 , b 3 ; (2) 判断数列 { b n } 是否为等比数列 , 并说明理由 ; (3) 求 { a n } 的通项公式 . - 24 - 考向一 考向二 考向三 考向四 考向五 解题心得 无论是求数列的通项还是求数列的前 n 项和 , 通过变形、整理后 , 能够把数列转化为等差数列或等比数列 , 进而利用等差数列或等比数列的通项公式或求和公式解决问题 . - 25 - 考向一 考向二 考向三 考向四 考向五 对点训练 5 (2018 河北唐山三模 , 文 17)已知数列{ a n }是等差数列,{ b n }是等比数列, a 1 = 1, b 1 = 2, a 2 +b 2 = 7, a 3 +b 3 = 13 . (1)求{ a n }和{ b n }的通项公式; - 26 - 考向一 考向二 考向三 考向四 考向五