高一数学（人教A版）必修2能力强化提升：1-1-2 圆柱、圆锥、圆台、球的结构特征、简单组合体的结构特征 8页

一、选择题 ‎1．下列说法不正确的是(　　)‎ A．圆柱的侧面展开图是一个矩形 B．圆锥过轴的截面是一个等腰三角形 C．直角三角形绕它的一条边旋转一周形成的曲面围成的几何体是圆锥 D．圆台平行于底面的截面是圆面 ‎[答案]　C ‎[解析]　由圆锥的概念知，直角三角形绕它的一条直角边所在直线旋转一周所围成的几何体是圆锥．强调一定要绕着它的一条直角边，即旋转轴为直角三角形的一条直角边所在的直线，因而C错．‎ ‎2．正方形绕其一条对角线所在直线旋转一周，所得几何体是(　　)‎ A．圆柱 B．圆锥 C．圆台 D．两个圆锥 ‎[答案]　D ‎3．下列说法正确的是(　　)‎ A．圆锥的母线长等于底面圆直径 B．圆柱的母线与轴垂直 C．圆台的母线与轴平行 D．球的直径必过球心 ‎[答案]　D ‎[解析]　‎ 圆锥的母线长与底面直径的大小不确定，则A项不正确；圆柱的母线与轴平行，则B项不正确；圆台的母线与轴相交，则C项不正确；很明显D项正确．‎ ‎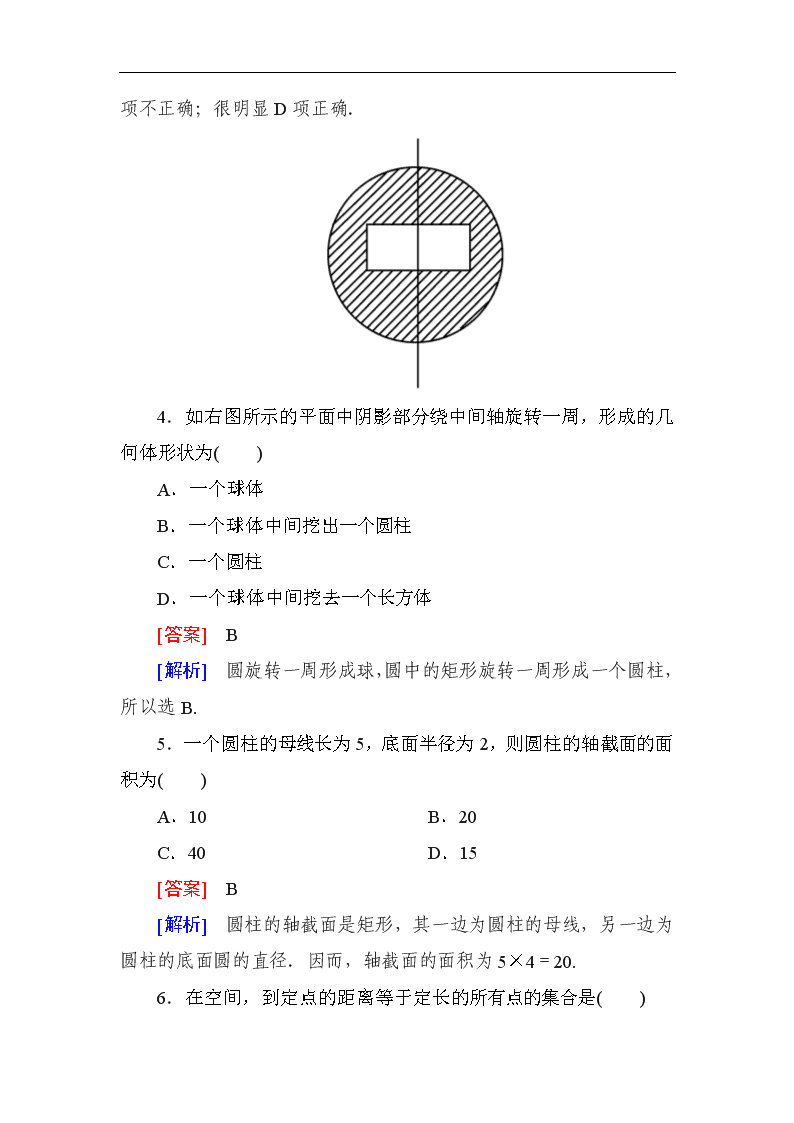4．如右图所示的平面中阴影部分绕中间轴旋转一周，形成的几何体形状为(　　)‎ A．一个球体 B．一个球体中间挖出一个圆柱 C．一个圆柱 D．一个球体中间挖去一个长方体 ‎[答案]　B ‎[解析]　圆旋转一周形成球，圆中的矩形旋转一周形成一个圆柱，所以选B.‎ ‎5．一个圆柱的母线长为5，底面半径为2，则圆柱的轴截面的面积为(　　)‎ A．10 B．20‎ C．40 D．15‎ ‎[答案]　B ‎[解析]　圆柱的轴截面是矩形，其一边为圆柱的母线，另一边为圆柱的底面圆的直径．因而，轴截面的面积为5×4＝20.‎ ‎6．在空间，到定点的距离等于定长的所有点的集合是(　　)‎ A．球 B．正方体 C．圆 D．球面 ‎[答案]　D ‎7．(2012－2013·南京模拟)经过旋转可以得到图1中几何体的是图2中的(　　)‎ ‎[答案]　A ‎[解析]　观察图中几何体的形状，掌握其结构特征，其上部为一个圆锥，下部是一个与圆锥同底的圆台，圆锥可由一直角三角形以过一直角边的直线为轴旋转一周得到，圆台可由一直角梯形绕过垂直于两底的腰的直线为轴旋转而成，通过上述判断再对选项中的平面图形适当分割，只有A适合．故正确答案为A.‎ ‎8．图中最左边的几何体由一个圆柱挖去一个以圆柱的上底面为底面，下底面圆心为顶点的圆锥而得．现用一个竖直的平面去截这个几何体，则截面图形可能是(　　)‎ A．(1)(2)　 B．(1)(3)　 C．(1)(4)　 D．(1)(5)‎ ‎[答案]　D ‎[解析]　圆锥除过轴的截面外，其它截面截圆锥得到的都不是三角形．‎ 二、填空题 ‎9．图①中的几何体叫做________，O叫它的________，OA叫它的________，AB叫它的________．‎ ‎[答案]　球　球心　半径　直径 ‎10．图②中的几何体叫________，AB、CD都是它的________，⊙O和⊙O′及其内部是它的________．‎ ‎　‎ ‎[答案]　圆柱　母线　底面 ‎11．图③中的几何体叫做________，SB为叫它的________．‎ ‎[答案]　圆锥　母线 ‎12．图④中的几何体叫做________，AA′叫它的________，⊙O′及其内部叫它的________，⊙O及其内部叫它的________，它还可以看作直角梯形OAA′O′绕它的________________旋转一周后，其他各边所形成的面所围成的旋转体．‎ ‎　‎ ‎[答案]　圆台　母线　上底面　下底面　垂直于两底的腰OO′‎ 三、解答题 ‎13．说出下列7种几何体的名称．‎ ‎[解析]　a是圆柱，b是圆锥，c是球，d、e是棱柱，f是圆台，g是棱锥．‎ ‎14．说出如图所示几何体的主要结构特征．‎ ‎[解析]　(1)是一个六棱柱中挖去一个圆柱；(2)是一个圆台与一个圆柱的组合体；(3)是两个四棱锥构成的组合体．‎ ‎15．如图所示，几何体可看作由什么图形旋转360°得到？画出平面图形和旋转轴．‎ ‎[解析]　先出画几何体的轴，然后再观察寻找平面图形．旋转前的平面图形如下：‎ ‎16．如图所示，在长方体ABCD－A′B′C′D′中，AB＝‎2 cm，AD＝‎4 cm，AA′＝‎3 cm.求在长方体表面上连接A、C′两点的诸曲线的长度的最小值．‎ ‎[解析]　将长方体的表面展开为平面图，这就将原问题转化为平面问题．本题所求必在下图所示的三个图中，从而，连接AC′的诸曲线中长度最小的为 cm(如图乙所示)．‎