河北省邯郸市2020届高三3月空中课堂备考检测数学（理）试题 23页

邯郸市2020年空中课堂高三备考检测 理科数学 同学们，在举国防控疫情期间，我们全民动员，同舟共济、共克时艰，显示了中华民族的伟大拼搏精神。作为高三学生，我们宅家备考，学会了人生的必修课——自律。岁月不蹉跎，未来才可期！努力充实丰盈自己，才能赢得胜利！‎ 本试卷分第I卷和第Ⅱ卷两部分。考生作答时，将答案答在答题卡上，在本试卷上答题无效。‎ 注意事项：‎ ‎1．答题前，务必先将自己的姓名、考号填写在答题卡上。‎ ‎2．答题时使用0.5毫米黑色签字笔或碳素笔书写，字体工整、笔迹清楚。‎ ‎3．请按照题号在各题的答题区域（黑色线框）内作答，超出答题区域书写的答案无效。‎ ‎4．保持卡面清洁，不折叠，不破损。 ‎ 第Ⅰ卷（60分）‎ 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．设复数，则在复平面内对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2．已知集合，则 A． B． C． D．‎ ‎3．的展开式第三项为 A． B． C． D．‎ ‎4．函数的部分图象大致为 ‎ ‎ ‎ A. B. C. 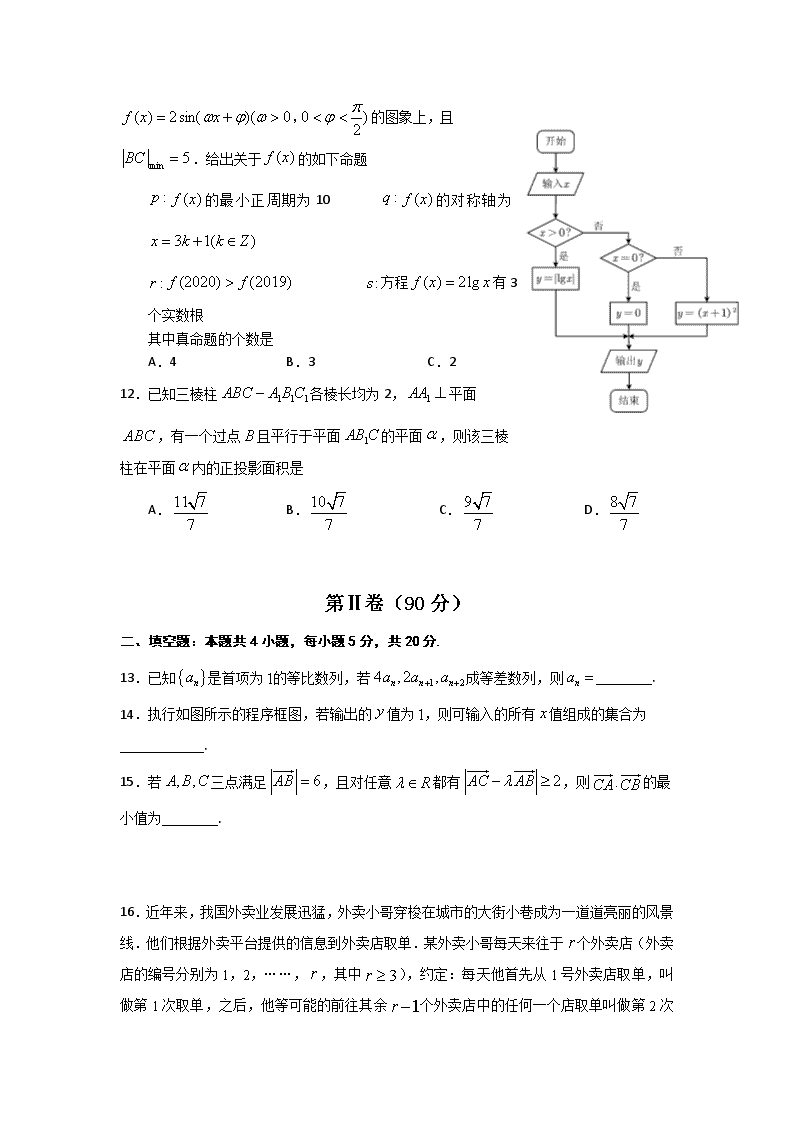D.‎ ‎5．设变量，满足约束条件则的最小值为 A．2 B． C．4 D． ‎ ‎6．公元前四世纪，毕达哥拉斯学派对数和形的关系进行了研究.他们借助几何图形（或格点）来表示数，称为形数.形数是联系算数和几何的纽带.图为五角形数的前4个，则第10个五角形数为 A．120 ‎ B．145 ‎ C．270 ‎ D．285‎ ‎7．若双曲线的一条渐近线与函数的图象相切，则该双曲线离心率为 A． B． C．2 D． ‎ ‎8．已知是定义在上的奇函数，其图象关于点对称，当时，则当时，的最小值为 A．0 B． C． D．‎ ‎9．设，为正数，且，则的最小值为 A． B． C． D．‎ ‎10．已知为抛物线的焦点.过点的直线交抛物线于两点，交准线于点.若，，则为 A． B． C． D．‎ ‎11．已知点在函数 的图象上，且．给出关于的如下命题 的最小正周期为10 的对称轴为 ‎ 方程有3个实数根 其中真命题的个数是 A．4 B．3 C．2 D．1‎ ‎12．已知三棱柱各棱长均为2，平面，有一个过点且平行于平面的平面，则该三棱柱在平面内的正投影面积是 A． B． C． D．‎ 第Ⅱ卷（90分）‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13．已知是首项为的等比数列，若成等差数列，则________. ‎ ‎14．执行如图所示的程序框图，若输出的值为，则可输入的所有值组成的集合为____________. ‎ ‎15．若三点满足，且对任意都有，则的最小值为________.‎ ‎16．近年来，我国外卖业发展迅猛，外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线．他们根据外卖平台提供的信息到外卖店取单．某外卖小哥每天来往于个外卖店（外卖店的编号分别为1，2，……，，其中），约定：每天他首先从1号外卖店取单，叫做第1次取单，之后，他等可能的前往其余 个外卖店中的任何一个店取单叫做第2次取单，依此类推．假设从第2次取单开始，他每次都是从上次取单的店之外的个外卖店取单．设事件第次取单恰好是从1号店取单，是事件发生的概率，显然，，则= ，与的关系式为 ．（）‎ 三、解答题：共70 分．解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：共60分。‎ ‎17．（12分）‎ 的内角的对边分别是，，.‎ ‎（1）求；‎ ‎（2）若成等差数列，求的面积.‎ ‎18．（12分）‎ 如图，在四棱锥中，底面，，点为的中点.平面交侧棱于点，四边形为平行四边形.‎ ‎（1）求证：平面平面；‎ ‎（2）若二面角的余弦值为，求与平面所成角的正弦值.‎ ‎ ‎ ‎19．（12分）‎ 中华猕猴桃果树喜湿怕旱，喜水怕涝，在我国种植范围较广.某地一生态农业公司建立了一个大型猕猴桃种植基地，该地区雨量充沛，阳光与温度条件也对果树的成长十分有利，但干旱或雨量过大也会造成损失.公司管理人员依据往年猕猴桃生长期30个周降雨量（单位：）的数据，得到如下茎叶图（表中的周降雨量为一周内降雨量的总和）.‎ 另外，猕猴桃果树发生灾害与周降雨量的关系如下表所示. ‎ 周降雨量 ‎（单位：）‎ 猕猴桃 灾害等级 轻灾 正常 轻灾 重灾 根据上述信息，解答如下问题.‎ ‎（1）根据茎叶图中所给的数据，写出周降雨量的中位数和众数；‎ ‎（2）以收集数据的频率作为概率.‎ ‎①估计该地区在今年发生重灾、轻灾以及无灾害的概率；‎ ‎②若无灾害影响，每亩果树获利6000元；若受轻灾害影响，则每亩损失 ‎5400元；若受重灾害影响则每亩损失10800元．为保护猕猴桃产业的发展，该地区农业部门有如下三种防控方案；‎ 方案1：防控到轻灾害，每亩防控费用400元.‎ 方案2：防控到重灾害，每亩防控费用1080元.‎ 方案3：不采取防控措施.‎ 问：如从获利角度考虑，哪种方案比较好？说明理由.‎ ‎20．（12分）‎ 已知椭圆过点且离心率为.‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若椭圆上存在三个不同的点，满足，求弦长的取值范围．‎ ‎21．（12分）‎ 已知函数．‎ ‎（1）当时，判断的单调性；‎ ‎（2）求证：．‎ ‎（二）选考题：共10 分。请考生从第22、23‎ ‎ 题中任选一题做答。并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分。‎ ‎22． [选修4-4：坐标系与参数方程]（10分）‎ 在平面直角坐标系中，点是曲线：（为参数）上的动点，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，以极点为中心，将线段顺时针旋转得到，设点的轨迹为曲线.‎ ‎（1）求曲线，的极坐标方程；‎ ‎（2）在极坐标系中，点的坐标为，射线与曲线分别交于两点，求的面积.‎ ‎23． [选修4-5：不等式选讲]（10分）‎ 已知函数.‎ ‎（1）当时，求的解集；‎ ‎（2）若在上恒成立，求的取值范围.‎ 邯郸市2020年空中课堂高三备考检测 理科数学 参考答案 一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．设复数，则在复平面内对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎1．答案：B 解析：，所以在复平面内对应的点位于第二象限．‎ ‎2．已知集合，则 A． B． C． D．‎ ‎2．答案：B 解析：‎ ‎3．的展开式第三项为 A． B． C． D．‎ ‎3．答案：C 解析：‎ ‎4．函数的部分图象大致为 ‎ ‎ ‎ A. B. C. D.‎ ‎4．答案: A 解析:因为，所以为奇函数，‎ 排除，当时，，排除，故选.‎ ‎5．设变量，满足约束条件则的最小值为 A．2 B． C．4 D． ‎ ‎5．答案：D 解析：画出可行域，可发现的最小值是到距离的平方.‎ ‎6．公元前四世纪，毕达哥拉斯学派对数和形的关系进行了研究.他们借助几何图形（或格点）来表示数，称为形数.形数是联系算数和几何的纽带.图为五角形数的前4个，则第10个五角形数为 A．120 ‎ B．145 ‎ C．270 ‎ D．285‎ ‎6．答案：B 解析：记第个五角形数为，由题意知：‎ 易知，由累加法得，所以.‎ ‎7．若双曲线的一条渐近线与函数的图象相切，则该双曲线离心率为 A． B． C．2 D． ‎ ‎7．答案：A 解析：因为双曲线的渐近线过原点，且方程为 函数图象也过原点，结合图形可知切点就是 ‎，‎ ‎8．已知是定义在上的奇函数，其图象关于点对称，当时，则当时，的最小值为 A．0 B． C． D．‎ ‎8．答案：A ‎ 解析：关于对称 ‎ ‎ 的周期为 时最小值即为时最小值 ‎ ‎ ‎，，选A ‎9．设，为正数，且，则的最小值为 A． B． C． D．‎ ‎9．答案：D 解析:当时，‎ ‎,‎ 因为，‎ 当且仅当，即时取等号，则．‎ ‎10．已知为抛物线的焦点.过点的直线交抛物线于两点，交准线于点.若，，则为 A． B． C． D．‎ ‎10．答案: C 解析:过做准线的垂线，垂足为轴与准线交点为，‎ 设，则，‎ ‎，因为，.‎ ‎11．已知点在函数的图象上，且．给出关于的如下命题 的最小正周期为10 的对称轴为 ‎ 方程有3个实数根 其中真命题的个数是 A．4 B．3 C．2 D．1‎ ‎ 11．答案：C ‎ 解析： ‎ ‎ ， ‎ ‎ ，所以为假命题 ‎ 对称轴为，所以为真命题 ‎，所以为假命题 方程有个根，所以为真命题 选C ‎ ‎ ‎12．已知三棱柱各棱长均为2，平面，有一个过点且平行于平面的平面，则该三棱柱在平面内的正投影面积是 A． B． C． D．‎ ‎12．答案：A 解析：‎ 投影面平移不影响正投影的形状和大小，所以我们就以平面为投影面，然后构造四棱柱，得到投影为五边形，通过计算可得正投影的面积为.‎ 二、填空题：本题共4小题，每小题5分，共20分.‎ ‎13．已知是首项为的等比数列，若成等差数列，则________. ‎ ‎13．答案：‎ 解析：‎ ‎14．执行如图所示的程序框图，若输出的值为，则可输入的所有值组成的集合为____________. ‎ ‎14．答案：‎ 解析：（1）当时，得 ‎（2）当时得，所以答案为 ‎15．若三点满足，且对任意都有，则的最小值为________.‎ ‎15．答案：‎ 解析：因为对任意都有，故点C到AB所在直线的距离为2‎ 设AB中点为M，则 当且仅当时等号成立 ‎16．近年来，我国外卖业发展迅猛，外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线．他们根据外卖平台提供的信息到外卖店取单．某外卖小哥每天来往于个外卖店（外卖店的编号分别为1，2，……，，其中），约定：每天他首先从1号外卖店取单，叫做第1次取单，之后，他等可能的前往其余个外卖店中的任何一个店取单叫做第2次取单，依此类推．假设从第2次取单开始，他每次都是从上次取单的店之外的个外卖店取单．设事件第次取单恰好是从1号店取单，是事件发生的概率，显然，，则= ，与的关系式为 ．（）‎ ‎16．答案：；‎ 解析：第2次取单恰好是从1号店取单，由于每天第1次取单都是从1号店开始，根据题意，第2次不可能从1号店取单，所以 ‎，，因此 三、解答题：共70 分．解答应写出文字说明、证明过程或演算步骤。第17~21题为必考题，每个试题考生都必须作答。第22、23题为选考题，考生根据要求作答。‎ ‎（一）必考题：共60分。‎ ‎17．（12分）‎ 的内角的对边分别是，，.‎ ‎（1）求；‎ ‎（2）若成等差数列，求的面积.‎ ‎17．解：‎ ‎ ‎ ‎ ‎ ‎18．（12分）‎ 如图，在四棱锥中，底面，，点为的中点.平面交侧棱于点，四边形为平行四边形.‎ ‎（1）求证：平面平面；‎ ‎（2）若二面角的余弦值为，求与平面所成角的正弦值.‎ ‎18．解：‎ ‎（1）证明：四边形为平行四边形.‎ ‎，又 ‎，又 点E为PC的中点 ‎·············1分 在直角梯形ABCD中，AB=AD=1，CD =2可得 连接BD，易得 ‎…………………………………………………………3分 又PC底面ABCD，BD平面ABCD BD平面PBC…………………………………………………………4分 BD平面PBD，‎ 平面PBD平面PBC………………………………………………5分 ‎（2）‎ 由（1）知CD=2，‎ 在直角梯形中可得DCB=‎ 又PC底面ABCD 以C为原点，CD为x轴，CP为z轴建立空间直角坐标系，如图所示……………6分 则设 BD平面PBC 平面PBC的法向量可取……………………………………7分 设平面ABP法向量为 由 得 可取…………………………………………………………8分 h=2…………………………………………………………………………9分 ‎， ……………………………………10分 PD与平面PAB所成角的正弦值为.…………………………………12分 ‎19．（12分）‎ 中华猕猴桃果树喜湿怕旱，喜水怕涝，在我国种植范围较广.某地一生态农业公司建立了一个大型猕猴桃种植基地，该地区雨量充沛，阳光与温度条件也对果树的成长十分有利，但干旱或雨量过大也会造成损失.公司管理人员依据往年猕猴桃生长期30个周降雨量（单位：）的数据，得到如下茎叶图（表中的周降雨量为一周内降雨量的总和）.‎ 另外，猕猴桃果树发生灾害与周降雨量的关系如下表所示. ‎ 周降雨量 ‎（单位：）‎ 猕猴桃 灾害等级 轻灾 正常 轻灾 重灾 根据上述信息，解答如下问题.‎ ‎（1）根据茎叶图中所给的数据，写出周降雨量的中位数和众数；‎ ‎（2）以收集数据的频率作为概率.‎ ‎①估计该地区在今年发生重灾、轻灾以及无灾害的概率；‎ ‎②若无灾害影响，每亩果树获利6000元；若受轻灾害影响，则每亩损失5400元；若受重灾害影响则每亩损失10800元．为保护猕猴桃产业的发展，该地区农业部门有如下三种防控方案；‎ 方案1：防控到轻灾害，每亩防控费用400元.‎ 方案2：防控到重灾害，每亩防控费用1080元.‎ 方案3：不采取防控措施.‎ 问：如从获利角度考虑，哪种方案比较好？说明理由.‎ ‎19．解：‎ ‎（1）根据茎叶图，可得中位数为12.5，众数为10 .….….…4分 ‎（2）①根据图中的数据，可得该地区周降雨量（单位：）的概率：‎ ‎，，，，‎ ‎，‎ 因此估计该地在今年发生重、轻害的概率分别为和 ，无灾害概率为……6分 ‎② 方案1：设每亩的获利为（元），则的可能取值为6000，-10800，则的分布列如下：‎ ‎6000‎ ‎-10800‎ 则(元)，则每亩净利润为（元）；‎ 方案2：设每亩的获利为（元），则的可能取值为6000元，于是，，净利润为（元）；‎ 方案3：设每亩的获利为（元），则的可能取值为6000，-5400，-10800，‎ 则的分布列如下：‎ ‎6000‎ ‎-5400‎ ‎-10800‎ 则(元)，于是每亩亏损为（元）；‎ 由此得出，方案一的获利最多，所以选择方案一比较好.……12分 ‎20．（12分）‎ 已知椭圆过点且离心率为.‎ ‎（1）求椭圆的标准方程；‎ ‎（2）若椭圆上存在三个不同的点,满足,求弦长的取值范围.‎ ‎20．解：‎ ‎（1）由题意知，又因为，解得.‎ 则椭圆标准方程为. ………………………………………4分 ‎（2）因为，则由向量加法的意义知四边形为平行四边形.‎ 设直线过两点，‎ ‎①若直线垂直于轴，易得：或者，‎ 此时. …………………………………………………………………5分 ‎ ‎②若直线不垂直于轴，设，，‎ 将直线代入的方程得 故， ……………………………………………………7分 ‎ 因为，所以，‎ 则，，即.‎ 因为在椭圆上，有，化简得. …………………9分 ‎ 验证，.‎ 所以 所以.………………………10分 ‎ 因为，则，即，得.‎ 综上可得，弦长的取值范围为． ………………………………………12分 ‎ ‎21．（12分）‎ 已知函数．‎ ‎（1）当时，判断的单调性；‎ ‎（2）求证：．‎ ‎21．解：‎ ‎（1）当时，，‎ 令，则在上为减函数，且 所以，当时， ，单调递增；‎ 当时， ，单调递减.‎ 故递增区间为；递减区间为 …………4分 ‎（2），‎ 只需证 ‎ 即 …………6分 易证成立. …………8分 记，则令，得 并且，当时，，单调递增；当时，，单调递减 所以， ‎ 即，命题得证. …………12分 ‎（二）选考题：共10 分。请考生从第22、23 题中任选一题做答。并用2B铅笔将答题卡上所选题目对应的题号右侧方框涂黑，按所涂题号进行评分；多涂、多答，按所涂的首题进行评分；不涂，按本选考题的首题进行评分。‎ ‎22． [选修4-4：坐标系与参数方程]（10分）‎ 在平面直角坐标系中，点是曲线：（为参数）上的动点，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，以极点为中心，将线段 顺时针旋转得到，设点的轨迹为曲线．‎ ‎（1）求曲线，的极坐标方程；‎ ‎（2）在极坐标系中，点的坐标为，射线与曲线分别交于两点，求的面积．‎ ‎22．解：‎ ‎（1）由题意可得的直角坐标方程为，‎ 其极坐标方程为........................2分 设点的极坐标为，则对应的点的极坐标为....................3分 又点在上，所以 即的极坐标方程为 ...................................................5分 ‎（2）由题意知点到射线的距离为，.......................7分 由（1）知的极坐标方程为，‎ ‎， ..........................9分 所以 ..................................................10分 ‎23． [选修4-5：不等式选讲]（10分）‎ 已知函数.‎ ‎（1）当时，求的解集；‎ ‎（2）若在上恒成立，求的取值范围.‎ ‎23．解：‎ ‎（1）当时，.‎ 当时，，此时的解集为；...................2分 当时，，此时的解集为 ‎；.......3分 当时，，此时的解集为.............................4分 综上所述的解集为................................................................................................5分 （2） 由（1）可知当时，在内恒成立；..............................................6分 当时，在内恒成立；..............7分 当时，在内，不满足在上恒成立的条件..............................................................................................................................9分 综上所述........................................................................................‎