【数学】河南省新乡市辉县市第二高级中学2019-2020学年高二下学期第五次月考（文）试卷 9页

河南省新乡市辉县市第二高级中学2019-2020学年 高二下学期第五次月考（文）试卷www.ks5u.com 一、单选题（每题5分，共60分）‎ ‎1．从集合的所有子集中，任取一个，这个集合恰是集合子集的概率是（　　）‎ A． B． C． D．‎ ‎2．下列函数中与函数为同一函数的是（ ）‎ A． B． C． D．‎ ‎3．命题“，”的否定为（ ）‎ A．， B．，‎ C．， D．，‎ ‎4．欧拉是科学史上一位最多产的杰出数学家，为数学界作出了巨大贡献，其中就有欧拉公式：（为虚数单位）.它建立了三角函数和指数函数间接关系，被誉为“数学中的天桥”.结合欧拉公式，则复数的模为（ ）‎ A． B． C． D．‎ ‎5．已知命题：，则；命题：，，则下列判断正确的是（ ）‎ A．是假命题 B．是假命题 ‎ C．是假命题 D．是真命题 ‎6．已知条件，条件，且是的充分不必要条件，则实数的值范围为（ ）‎ A． B． C． D．‎ ‎7．已知是定义在上的偶函数,且在上是减函数,设,‎ ‎,,则的大小关系是（ ）‎ A． B． C． D．‎ ‎8．函数y=sin2x的图象可能是（ ）‎ A． B． C． D．‎ ‎9．已知函数定义域为，则实数的取值范围是（ ）‎ A． B． C． D．‎ ‎10．已知函数是定义在上的偶函数，且满足，且当时，，则（ ）‎ A． B． C． D．‎ ‎11．已知定义域为的函数在单调递增，且为偶函数，若，则不等式的解集为（ ）‎ A． B． C． D．‎ ‎12．已知函数（a＞0且a≠1）是R上的单调函数，则a的取值范围是（ ）‎ A．（0，] B．[） C．[] D．（]‎ 二、填空题（每题5分，共20分）‎ ‎13．已知函数，则______.‎ ‎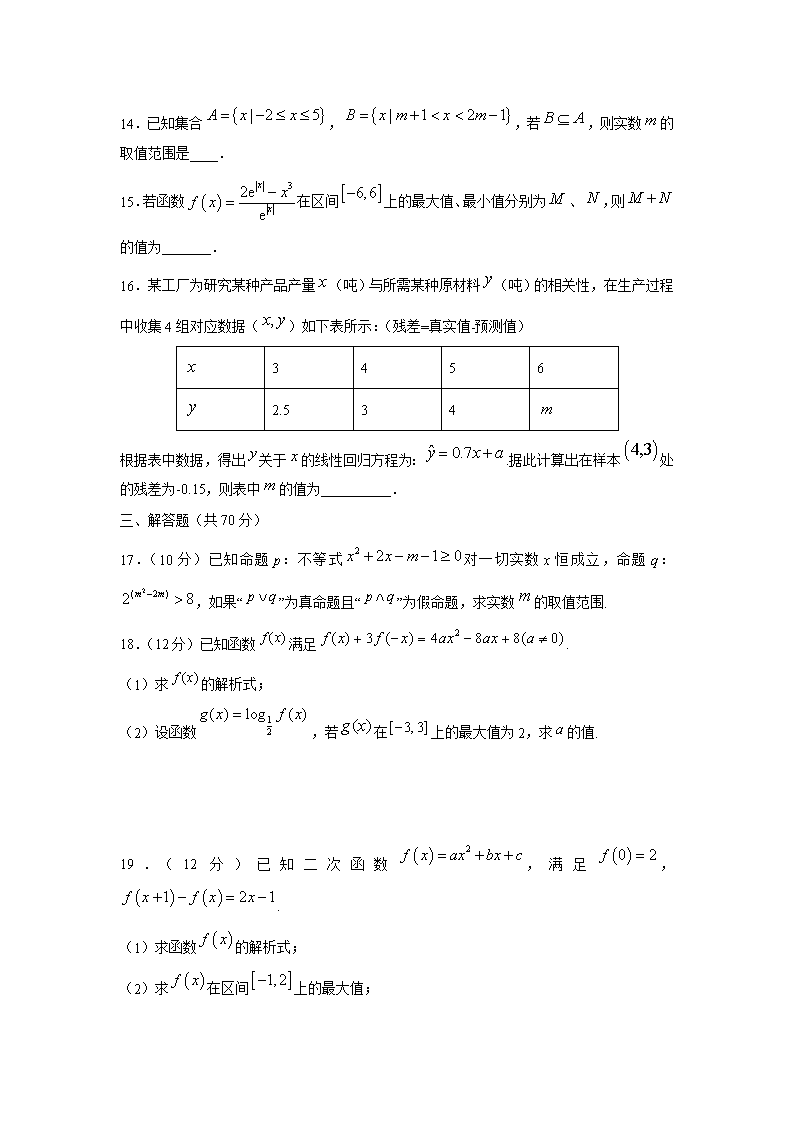14．已知集合，，若，则实数的取值范围是____．‎ ‎15．若函数在区间上的最大值、最小值分别为、，则 的值为_______．‎ ‎16．某工厂为研究某种产品产量（吨）与所需某种原材料（吨）的相关性，在生产过程中收集4组对应数据（）如下表所示：（残差=真实值-预测值）‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎2.5‎ ‎3‎ ‎4‎ 根据表中数据，得出关于的线性回归方程为：.据此计算出在样本处的残差为-0.15，则表中的值为__________．‎ 三、解答题（共70分）‎ ‎17．（10分）已知命题p：不等式对一切实数x恒成立，命题q：，如果“”为真命题且“”为假命题，求实数的取值范围.‎ ‎18．（12分）已知函数满足.‎ ‎（1）求的解析式；‎ ‎（2）设函数，若在上的最大值为2，求的值.‎ ‎19．（12分）已知二次函数，满足，.‎ ‎（1）求函数的解析式；‎ ‎（2）求在区间上的最大值；‎ ‎（3）若函数在区间上单调，求实数的取值范围.‎ ‎20．（12分）在直角坐标系中，曲线的参数方程为（为参数），以坐标原点为极点，以轴正半轴为极轴，建立极坐标系，曲线的极坐标方程为.‎ ‎（1）写出的普通方程和的直角坐标方程；‎ ‎（2）设点在上，点在上，求的最小值以及此时的直角坐标.‎ ‎21．（12分）在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立坐标系，曲线的方程，，过点的直线的参数方程为（为参数）.‎ ‎（1）求直线的普通方程与曲线的直角坐标方程；‎ ‎（2）若直线与曲线交于、两点，求的值.‎ ‎22．（12分）今年1月至2月由新型冠状病毒引起的肺炎病例陡然增多，为了严控疫情传播，做好重点人群的预防工作，某地区共统计返乡人员人，其中岁及以上的共有人.这人中确诊的有名，其中岁以下的人占.‎ 确诊患新冠肺炎 未确诊患新冠肺炎 合计 ‎50岁及以上 ‎40‎ ‎50岁以下 合计 ‎10‎ ‎100‎ ‎（1）试估计岁及以上的返乡人员感染新型冠状病毒引起的肺炎的概率；‎ ‎（2）请将下面的列联表补充完整，并判断是否有％的把握认为是否确诊患新冠肺炎与年龄有关；‎ 参考表：‎ ‎0.10‎ ‎0.05‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 参考公式：，其中.‎ ‎【参考答案】‎ 一、选择题 ‎1．C 2．D 3．A 4．B 5．D 6．A 7．D 8．D 9．C 10．A 11．A 12．C 二、填空题 ‎13． ； 14． 15． 16．‎ 三、解答题 ‎17．【解】当命题为真时，由恒成立得：‎ ‎，解得：；‎ 当命题为真时：由得：，解得：或.‎ 由“”为假命题且“”为真命题得：命题为一真一假，‎ 当真假时，，解集为空集；‎ 当假真时，，解得：或；‎ 综上所述：实数的取值范围是：.‎ ‎18．【解】（1）因为，‎ 用代替上式中的，故可得，‎ 故可得.‎ ‎（2）由（1）中所求，故可得 的对称轴，当时，要满足题意，‎ 只需：在区间上恒大于零，‎ 又此时在区间单调递增，在区间单调递减，‎ 则还需，故且即可.‎ 则，且，解得.‎ 当时，要满足题意，只需在区间上恒大于零，‎ 又此时在区间单调递减，在区间单调递增，‎ 则还需，故且.‎ 又，故可得；‎ ‎，‎ 显然当时，，故，‎ 故还需，解得满足题意. ‎ 综上所述，满足题意的或.‎ ‎19．【解】（1）由，得，‎ 由，得，‎ 故，解得，所以.‎ ‎（2）由（1）得：，则的图象的对称轴方程为，‎ 又，，所以当时在区间上取最大值为5.‎ ‎（3）由于函数在区间上单调，‎ 因为的图象的对称轴方程为，所以或，‎ 解得：或，因此的取值范围为：.‎ ‎20．【解】（1）的普通方程为，的直角坐标方程为.‎ ‎（2）由题意，可设点的直角坐标为，‎ 因为是直线，所以的最小值即为到的距离的最小值，‎ ‎.‎ 当且仅当时，取得最小值，最小值为，‎ 此时的直角坐标为.‎ ‎21．【解】（1）因为曲线的方程，，‎ 故可得，即；‎ 因为直线的参数方程为（为参数），‎ 消去参数，则其直角方程为.‎ ‎（2）将直线参数方程代入曲线的直角方程，可得，‎ 设点对应的参数，则，‎ 故可得.‎ 故弦长.‎ ‎22．【解】（1）因为人中确诊的有名，岁以下的人占，‎ 所以岁以下的确诊人数为，岁及以上确诊人数为，‎ 因为岁及以上的共有人，‎ 所以岁及以上的返乡人员感染新型冠状病毒引起的肺炎的频率为.‎ ‎（2）列联表补充如下：‎ 确诊患新冠肺炎 未确诊患新冠肺炎 合计 ‎50岁以上 ‎7‎ ‎33‎ ‎40‎ ‎50岁以下 ‎3‎ ‎57‎ ‎60‎ 合计 ‎10‎ ‎90‎ ‎100‎ ‎.‎ 所以有%的把握认为是否确诊患新冠肺炎与年龄有关.‎