2021版高考数学一轮复习核心素养测评五十九曲线与方程（含轨迹问题）理北师大版 10页

核心素养测评五十九 曲线与方程（含轨迹问题）‎ ‎(30分钟　60分)‎ 一、选择题(每小题5分,共25分)‎ ‎1.动圆M经过双曲线x2-=1的左焦点且与直线x=2相切,则圆心M的轨迹方程是 (　　)‎ A.y2=8x　　　　　 B.y2=-8x C.y2=4x D.y2=-4x ‎【解析】选B.双曲线x2-=1的左焦点为F(-2,0),动圆M经过点F且与直线x=2相切,则圆心M到点F的距离和到直线x=2的距离相等,由抛物线的定义知轨迹是抛物线,其方程为y2=-8x.‎ ‎2.在平面直角坐标系中,已知两点A(3,1),B(-1,3),若点C满足=λ1‎ ‎+λ2(O为原点),其中λ1,λ2∈R,且λ1+λ2=1,则点C的轨迹是 (　　)‎ A.直线 B.椭圆 C.圆 D.双曲线 ‎【解析】选A.设C(x,y),则=(x,y),=(3,1),=(-1,3),‎ 因为=λ1+λ2,‎ 所以 又因为λ1+λ2=1,所以化简得x+2y-5=0表示一条直线.‎ ‎3.已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则Q点的轨迹方程是 (　　)‎ A.2x+y+1=0 B.2x-y-5=0‎ C.2x-y-1=0 D.2x-y+5=0‎ ‎【解析】选D.设Q(x,y),则P为(-2-x,4-y),代入2x-y+3=0,得Q点的轨迹方程为2x-y+5=0.‎ ‎4.在△ABC中,B(-2,0),C(2,0),A(x,y),给出△ABC满足的条件,就能得到动点A的轨迹方程.如表给出了一些条件及方程:‎ 条件 方程 - 10 -‎ ‎①△ABC周长为10‎ C1:y2=25‎ ‎②△ABC面积为10‎ C2:x2+y2=4(y≠0)‎ ‎③△ABC中,∠A=90°‎ C3:+=1(y≠0)‎ 则满足条件①,②,③的轨迹方程依次为 (　　)‎ A.C3,C1,C2 B.C1,C2,C3‎ C.C3,C2,C1　 D.C1,C3,C2‎ ‎【解析】选A.①△ABC的周长为10,‎ 即|AB|+|AC|+|BC|=10,‎ 又|BC|=4,所以|AB|+|AC|=6>|BC|,此时动点A的轨迹为椭圆,与C3对应;‎ ‎②△ABC的面积为10,所以|BC|·|y|=10即|y|=5与C1对应;‎ ‎③因为∠A=90°,所以·=(-2-x,-y)·(2-x,-y)=x2+y2-4=0与C2对应.‎ ‎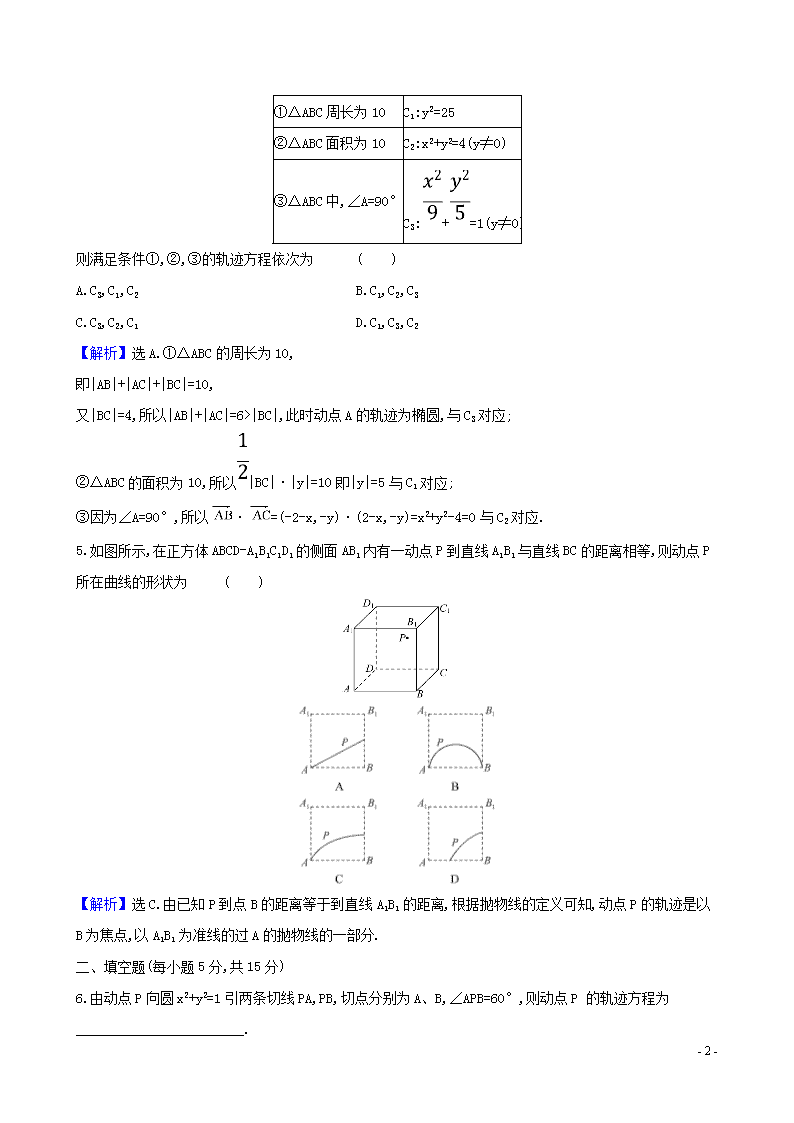5.如图所示,在正方体ABCD-A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为 (　　)‎ ‎【解析】选C.由已知P到点B的距离等于到直线A1B1的距离,根据抛物线的定义可知,动点P的轨迹是以B为焦点,以A1B1为准线的过A的抛物线的一部分.‎ 二、填空题(每小题5分,共15分)‎ ‎6.由动点P向圆x2+y2=1引两条切线PA,PB,切点分别为A、B,∠APB=60°,则动点P 的轨迹方程为________________________. ‎ - 10 -‎ ‎【解析】设P(x,y),x2+y2=1的圆心为O,因为∠APB=60°,OP平分∠APB,所以 ‎∠OPB=30°,因为|OB|=1,∠OBP为直角,所以|OP|=2,所以x2+y2=4.‎ 答案:x2+y2=4‎ ‎7.在平面直角坐标系中,动点P和点M(-2,0),N(2,0)满足||||+·=0,则动点P(x,y)的轨迹方程为________________________________. ‎ ‎【解析】把已知等式||||+·=0用坐标表示,得4+4(x-2)=0,化简变形得y2=-8x.‎ 答案:y2=-8x ‎8.若直线y=k(x+2)+4与曲线y=有两个交点,则实数k的取值范围是________________.  ‎ ‎【解析】直线y=k(x+2)+4,当x=-2时,y=4,可得此直线恒过A(-2,4),曲线y=为圆心在坐标原点,半径为2的半圆,根据题意作出相应的图形,如图所示:‎ 当直线y=k(x+2)+4与半圆相切(切点在第一象限)时,圆心到直线的距离d=r,‎ 所以=2,即4k2+16k+16=4+4k2,‎ 解得:k=-,当直线y=k(x+2)+4过点C时,‎ 将x=2,y=0代入直线方程得:4k+4=0,‎ 解得:k=-1,‎ 则直线与曲线有2个交点时k的取值范围为.‎ - 10 -‎ 答案:‎ 三、解答题(每小题10分,共20分)‎ ‎9.在平面直角坐标系中,已知A1(-,0),A2(,0),P(x,y),M(x,1),N(x,-2),若实数λ使得λ2·=·(O为坐标原点).求P点的轨迹方程,并讨论P点的轨迹类型.‎ ‎【解析】=(x,1),=(x,-2),=(x+,y),=(x-,y).‎ 因为λ2·=·,所以(x2-2)λ2=x2-2+y2,‎ 整理得(1-λ2)x2+y2=2(1-λ2).‎ ‎①当λ=±1时,方程为y=0,轨迹为一条直线;‎ ‎②当λ=0时,方程为x2+y2=2,轨迹为圆;‎ ‎③当λ∈(-1,0)∪(0,1)时,方程为+=1,轨迹为中心在原点,焦点在x轴上的椭圆;‎ ‎④当λ∈(-∞,-1)∪(1,+∞)时,方程为-=1,轨迹为中心在原点,焦点在x轴上的双曲线.‎ ‎10.(2020·成都模拟)已知长度为4的线段AB的两个端点A,B分别在x轴和y轴上运动,动点P满足=3,记动点P的轨迹为曲线C. ‎ ‎(1)求曲线C的方程.‎ ‎(2)设不经过点H(0,1)的直线y=2x+t与曲线C相交于两点M,N.若直线HM与HN的斜率之和为1,求实数t的值.‎ ‎【解析】(1)设P(x,y),A(m,0),B(0,n),‎ 因为=3,‎ 所以(x,y-n)=3(m-x,-y)=(3m-3x,-3y),‎ 即 ,所以 ,‎ - 10 -‎ 因为|AB|=4,‎ 所以m2+n2=16,‎ 所以x2+16y2=16,‎ 所以曲线C的方程为:+y2=1;‎ ‎(2)设M(x1,y1),N(x2,y2),‎ 由 ,消去y得,‎ ‎37x2+36tx+9(t2-1)=0,‎ 由Δ=(36t)2-4×37×9(t2-1)>0,‎ 可得-0得k2<,所以0