高中数学（人教A版）必修5能力强化提升及单元测试：1-2第1课时 5页

‎1.2 应用举例　‎ 第1课时　正、余弦定理在实际问题中 的应用 双基达标　(限时20分钟) ‎1．某人先向正东方向走了x km，然后他向右转150°，向新的方向走了3 km，结果他离出发点恰好为 km，那么x的值为 (　　)．‎ A. B．2 C．2或 D．3‎ 解析　根据余弦定理可得，()2＝x2＋32－2×3xcos(180°－150°)，即x2－3x＋6＝0，∴x＝2或.‎ 答案　C ‎2．从200 m高的山顶看，测得山下一塔顶与塔底的俯角分别为30°，60°，则塔高为(　　)．‎ A. m B. m C. m D. 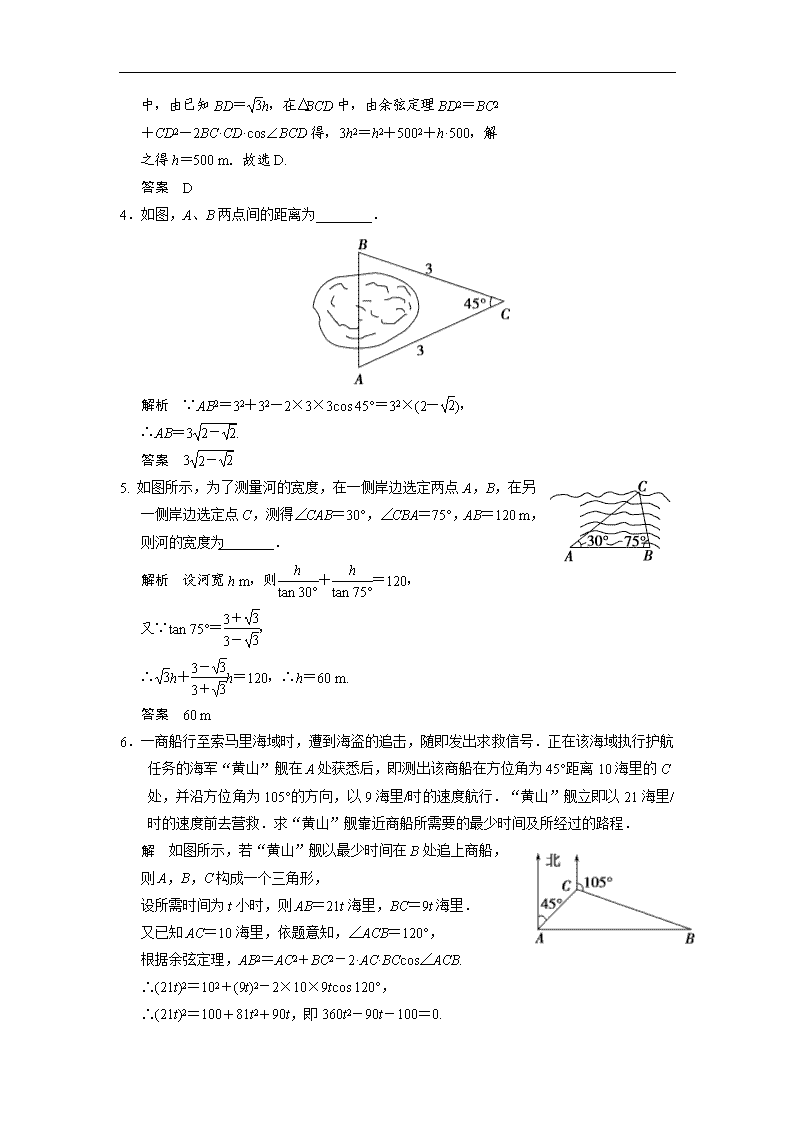m 解析　由山顶与塔底的俯角为60°可知，山脚与塔底的水平距离为，又山顶看塔顶的俯角为30°，设塔高为x m，则200－x＝×，∴x＝ m．故选A.‎ 答案　A ‎3．要测量底部不能到达的东方明珠电视塔的高度，在黄浦江西岸选择甲、乙两观测点，在甲、乙两点分别测得塔顶的仰角分别为45°，30°，在水平面上测得电视塔与甲地连线及甲、乙两地连线所成的角为120°，甲、乙两地相距500 m，则电视塔在这次测量中的高度是 (　　)．‎ A．100 m B．400 m C．200 m D．500 m 解析 由题意画出示意图，‎ 设高AB＝h，在Rt△ABC中，由已知BC＝h，在Rt△ABD ‎ 中，由已知BD＝h，在△BCD中，由余弦定理BD2＝BC2‎ ‎＋CD2－2BC·CD·cos∠BCD得，3h2＝h2＋5002＋h·500，解 之得h＝500 m．故选D.‎ 答案　D ‎4．如图，A、B两点间的距离为________．‎ 解析　∵AB2＝32＋32－2×3×3cos 45°＝32×(2－)，‎ ‎∴AB＝3.‎ 答案　3 ‎5. 如图所示，为了测量河的宽度，在一侧岸边选定两点A，B，在另一侧岸边选定点C，测得∠CAB＝30°，∠CBA＝75°，AB＝120 m，则河的宽度为________．‎ 解析　设河宽h m，则＋＝120，‎ 又∵tan 75°＝，‎ ‎∴h＋h＝120，∴h＝60 m.‎ 答案　60 m ‎6．一商船行至索马里海域时，遭到海盗的追击，随即发出求救信号．正在该海域执行护航任务的海军“黄山”舰在A处获悉后，即测出该商船在方位角为45°距离10海里的C处，并沿方位角为105°的方向，以9海里/时的速度航行．“黄山”舰立即以21海里/时的速度前去营救．求“黄山”舰靠近商船所需要的最少时间及所经过的路程．‎ 解 如图所示，若“黄山”舰以最少时间在B处追上商船， ‎ 则A，B，C构成一个三角形，‎ 设所需时间为t小时，则AB＝21t海里，BC＝9t海里．‎ 又已知AC＝10海里，依题意知，∠ACB＝120°，‎ 根据余弦定理，AB2＝AC2＋BC2－2·AC·BCcos∠ACB.‎ ‎∴(21t)2＝102＋(9t)2－2×10×9tcos 120°，‎ ‎∴(21t)2＝100＋81t2＋90t，即360t2－90t－100＝0.‎ ‎∴t＝或t＝－(舍)．‎ ‎∴AB＝21×＝14(海里)．‎ 即“黄山”舰需要用小时靠近商船，共航行14海里．‎ 综合提高 （限时25分钟）‎ ‎7．已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为 (　　)．‎ A．a km B.a km C.a km D．2a km 解析　在△ABC中，AB＝BC＝a km，∠ACB＝180°－(20°＋40°)＝120°，‎ ‎∴AB＝ ‎＝ ＝a (km)．‎ 答案　B ‎8．有一长为10 m的斜坡，倾斜角为75°，在不改变坡高和坡顶的前提下，通过加长坡面的方法将它的倾斜角改为30°，则坡底要延长 (　　)．‎ A．5 m B．10 m C．10 m D．10 m 解析　如图，设将坡底加长到B′时，倾斜角为30°.‎ 依题意，∠B′＝30°，∠BAB′＝75°－30°＝45°，AB＝10 m，‎ 在△ABB′中，根据正弦定理，得 BB′＝＝＝10 (m)，‎ 即当坡底伸长10 m时，斜坡的倾斜角将变为30°.‎ 答案　C ‎9．已知A，B两岛相距10 n mile，从A岛看B，C两岛的视角为60°，从B岛看A，C两岛的视角是75°，则B，C两岛的距离为________ n mile.‎ 解析　A，B，C为△ABC的顶点，且A＝60°，B＝75°，‎ ‎∴C＝180°－(A＋B)＝180°－(60°＋75°)＝45°.‎ 根据正弦定理得，‎ BC＝＝＝5 (n mile)．‎ 答案　5 ‎10．某海岛周围38海里有暗礁，一轮船由西向东航行，初测此岛在北偏东60°方向，航行30海里后测得此岛在东北方向，若不改变航向，则此船________触礁的危险(填“有”或“无”)．‎ 解析　由题意在三角形ABC中，AB＝30，∠BAC＝30°，‎ ‎∠ABC＝135°，∴∠ACB＝15°，由正弦定理BC＝·‎ sin∠BAC＝·‎ sin 30°＝＝15(＋)．‎ 在Rt△BDC中，CD＝BC＝15(＋1)>38.‎ 答案　无 ‎11.为了测量两山顶M、N间的距离，飞机沿水平方向在A、B两点进行测量，A、B、M、N在同一个铅垂平面内，如图，飞机能测量的数据有俯角和A、B间的距离，请设计一个方案；包括：①指出需要测量的数据(用字母表示，并在图中标出)；②用文字和公式写出计算M、N间的距离的步骤．‎ 解　①需要测量的数据有A到M、N的俯角α1、β1，B到M、N的俯角α2、β2，A、B的距离d(如图所示)．‎ ‎②方案一：第一步：计算AM，由正弦定理AM＝；‎ 第二步：计算AN，由正弦定理AN＝；‎ 第三步：计算MN，由余弦定理 MN＝.‎ 方案二：第一步：计算BM，由正弦定理BM＝；‎ 第二步：计算BN，由正弦定理BN＝；‎ 第三步：计算MN，由余弦定理 MN＝.‎ ‎12．(创新拓展)某海上养殖基地A接到气象部门预报，位于基地南偏东60°距离20(＋1)海里的海面上有一台风中心，影响半径为20海里，正以每小时10海里的速度沿某一方向匀速直线前进，预计台风中心将从基地东北方向刮过且(＋1)小时后开始影响基地持续2小时．求台风移动的方向．‎ 解　如题图所示，设预报时台风中心为B，开始影响基地时台风中心为C，则B，C，D在同一直线上，且AD＝20海里，AC＝20海里．‎ 由题意知，AB＝20(＋1) 海里，DC＝2×10＝20 海里，BC＝(＋1)×10 海里．‎ 在△ADC中，∵DC2＝AD2＋AC2，‎ ‎∴∠DAC＝90°，∠ADC＝45°.‎ 在△ABC中，由余弦定理得 cos∠BAC＝＝，‎ ‎∴∠BAC＝30°，‎ 又∵B位于A的南偏东60°，且60°＋30°＋90°＝180°，‎ ‎∴D位于A的正北方向，又∵∠ADC＝45°，‎ ‎∴台风移动的方向为的方向，即北偏西45°方向．‎ 所以台风向北偏西45°方向移动．‎