2019届二轮复习数形结合思想课件（37张）（全国通用） 37页

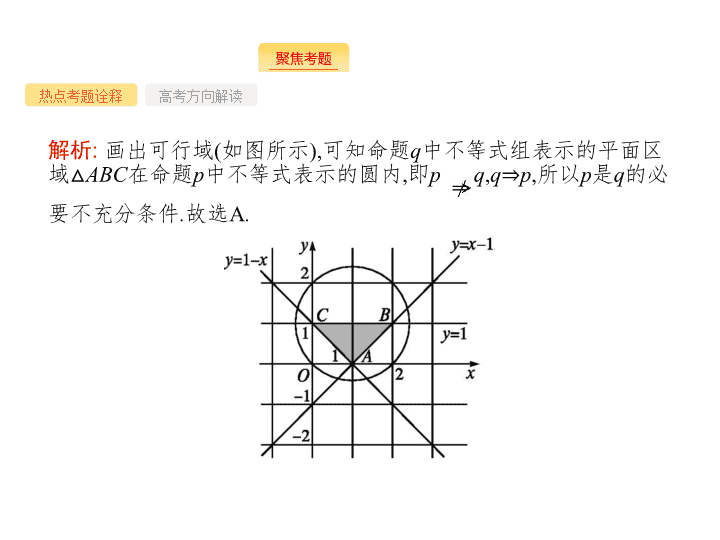
第 2 讲　数形结合思想 - 2 - 热点考题诠释 高考方向解读 1 . (2016 四川 , 理 7) 设 p : 实数 x , y 满足 ( x- 1) 2 + ( y- 1) 2 ≤ 2, q : 实数 x , y 满足 A . 必要不充分条件 B. 充分不必要条件 C. 充要条件 D. 既不充分也不必要条件 A 　 - 3 - 热点考题诠释 高考方向解读 解析 : 画出可行域 ( 如图所示 ), 可知命题 q 中不等式组表示的平面区域 △ ABC 在命题 p 中不等式表示的圆内 , 即 p q , q ⇒ p , 所以 p 是 q 的必要不充分条件 . 故选 A . - 4 - 热点考题诠释 高考方向解读 C - 5 - 热点考题诠释 高考方向解读 解析 : 画出不等式 组 表示 的平面区域如图阴影部分所示 . 作出直线 x+y- 2 = 0 . 设直线 x- 3 y+ 4 = 0 与 x+y= 0 的交点为 C , 直线 x= 2 与直线 x+y= 0 的交点为 D. 过 C 作 CA ⊥ 直线 x+y- 2 = 0 于点 A , 过 D 作 DB ⊥ 直线 x+y- 2 = 0 于点 B , 则区域中的点在直线 x+y- 2 = 0 上的投影为 AB. - 6 - 热点考题诠释 高考方向解读 - 7 - 热点考题诠释 高考方向解读 A 　 - 8 - 热点考题诠释 高考方向解读 - 9 - 热点考题诠释 高考方向解读 - 10 - 热点考题诠释 高考方向解读 4 . (2016 山东 , 理 15) 已知 函数 其中 m> 0, 若存在实数 b , 使得关于 x 的方程 f ( x ) =b 有三个不同的根 , 则 m 的取值范围是 　　　　　 .   (3, +∞ ) 　 - 11 - 热点考题诠释 高考方向解读 解析 : x 2 - 2 mx+ 4 m= ( x-m ) 2 + 4 m-m 2 . 由题意画出函数图象为下图时才符合 , 要满足存在实数 b , 使得关于 x 的方程 f ( x ) =b 有三个不同的根 , 应 4 m-m 2 3, 即 m 的取值范围为 (3, +∞ ) . - 12 - 热点考题诠释 高考方向解读 数形结合的思想在每年的高考中都有所体现 , 它常用来 : 研究方程根的情况 , 讨论函数的值域 ( 最值 ) 及求变量的取值范围等 . 对以上内容的选择题、填空题 , 数形结合特别有效 . 从今年的高考题来看 , 数形结合的重点是研究 “ 以形助数 ”, 因此 “ 以数定形 ” 在今后的高考中将会有所加强 , 应引起重视 , 复习中应提高用数形结合思想解题的意识 , 画图不能太草 , 要善于用特殊数或特殊点来精确确定图形间的位置关系 . 考向预测 : 在浙江省新高考中 , 数形结合思想主要在函数、导数、不等式等问题中体现 , 在选择题、填空题甚至解答题中都要善于利用数形结合思想 “ 以形助数 ”“ 以数定形 ” . - 13 - 命题热点一 命题 热点二 命题 热点三 利用数形结合讨论方程的解或图象的交点 ( 热度 : ★★★ ) 例 1 已知定义在 R 上的偶函数 f ( x ) 满足 f ( x- 4) =f ( x ), 且在区间 [0,2] 上 f ( x ) =x , 若关于 x 的方程 f ( x ) = log a x 有三个不同的实根 , 则 a 的取值范围是 　　　　　 .   - 14 - 命题热点一 命题 热点二 命题 热点三 - 15 - 命题热点一 命题 热点二 命题 热点三 规律方法 用函数的图象讨论方程 ( 特别是含参数的指数、对数、根式、三角函数等复杂方程 ) 的解的个数是一种重要的思想方法 , 其基本思想是先把方程两边的代数式看作是两个熟悉函数的表达式 ( 不熟悉时 , 需要作适当变形转化为两个熟悉的函数 ), 然后在同一坐标系中作出两个函数的图象 , 图象的交点个数即为方程解的个数 . - 16 - 命题热点一 命题 热点二 命题 热点三 迁移训练 1 　 已知函数 y=|x 2 - 1 | 的图象与函数 y=kx 2 - ( k+ 2) x+ 2 的图象恰有两个不同的公共点 , 则实数 k 的取值范围为 　　　　　　　　　　　 .   k ≤ 0 或 k= 1 或 k ≥ 4 直线 y=kx- 2 过定点 (0, - 2), 观察图象可知 , 当直线与函数图象只有一个公共点时 , 即直线的斜率 k 的取值范围使其只有一个交点 , 由图即可知 k 的取值范围为 k ≤ 0 或 k= 1 或 k ≥ 4 . - 17 - 命题热点一 命题热点二 命题 热点三 利用数形结合解不等式或求参数 ( 热度 : ★★☆ ) 例 2 若关于 x 的不等式 4 a x- 1 < 3 x- 4( a> 0, 且 a ≠1) 对于任意的 x> 2 恒成立 , 求 a 的取值范围 . - 18 - 命题热点一 命题热点二 命题 热点三 - 19 - 命题热点一 命题热点二 命题 热点三 规律方法 解含参数的不等式时 , 由于涉及参数 , 往往需要讨论 , 导致运算过程烦琐冗长 . 如果题设与几何图形有联系 , 那么利用数形结合的方法 , 问题将会顺利地得到解决 . - 20 - 命题热点一 命题热点二 命题 热点三 迁移训练 2 　 若不等式 |x- 2 a| ≥ x+a- 1 对 x ∈ R 恒成立 , 则 a 的取值范围是 　　　　　 .   - 21 - 命题热点一 命题 热点二 命题热点三 C - 22 - 命题热点一 命题 热点二 命题热点三 - 23 - 命题热点一 命题 热点二 命题热点三 - 24 - 命题热点一 命题 热点二 命题热点三 - 25 - 命题热点一 命题 热点二 命题热点三 规律方法 利用数形结合求最值的方法步骤 第一步 : 分析数理特征 , 确定目标问题的几何意义 . 一般从图形结构、图形的几何意义分析代数式是否具有几何意义 . 第二步 : 转化为几何问题 . 第三步 : 解决几何问题 . 第四步 : 回归代数问题 . 第五步 : 回顾反思 . 应用几何意义数形结合法解决问题需要熟悉常见的几何结构的代数形式 , 主要有 :(1) 比值 —— 可考虑直线的斜率 ;(2) 二元一次式 —— 可考虑直线的截距 ;(3) 根式分式 —— 可考虑点到直线的距离 ;(4) 根式 —— 可考虑两点间的距离 . - 26 - 命题热点一 命题 热点二 命题热点三 B - 27 - 命题热点一 命题 热点二 命题热点三 - 28 - 易错点一 易错 点二 图形性错误 对于方程或不等式一定要注意同时开方或平方后与原式是否等价 , 不注意此点 , 易造成丢解或增解 . 例 1 关于 x 的 方程 - x-m= 0 有解 , 则实数 m 的取值范围为 　　　　　 .   - 29 - 易错点一 易错 点二 - 30 - 易错点一 易错点二 观察图象不全面致误 利用数形结合思想解题 , 关键是在图形变化过程中准确寻求临界点 , 满足条件的情形要找全 , 找准 , 而不能因观察图象不全导致失误 . - 31 - 易错点一 易错点二 例 2 已知 y=f ( x ) 是以 2 为周期的偶函数 , 当 x ∈ [0,1] 时 , f ( x ) =x , 那么在区间 [ - 1,3] 内 , 关于 x 的方程 f ( x ) =kx+k+ 1( k ∈ R , k ≠1) 有 4 个根 , 则 k 的取值范围为 　　　　　 .   - 32 - 易错点一 易错点二 解析 : 如图所示 , 画出 y=f ( x ) 在 [ - 1,3] 上的简图 , 又 f ( x ) =kx+k+ 1 =k ( x+ 1) + 1 为恒过点 ( - 1,1) 的直线系 , 根据图象可知 , 在 l 1 , l 2 之间的直线都满足与函数图象在区间 [ - 1,3] 上有 4 个交点 , 结合图象可知 k 的取值范围 为 点评 本题易出现观察图象不仔细 , 误认为满足条件的情况为 l 3 到 l 2 之间而造成错解 . - 33 - 1 2 3 4 5 A 　 - 34 - 1 2 3 4 5 2 . 若两个非零向量 a , b 满足 | a + b |=| a - b |= 2 | a | , 则向量 a + b 与 a - b 的夹角是 ( 　　 ) C - 35 - 1 2 3 4 5 B - 36 - 1 2 3 4 5 C - 37 - 1 2 3 4 5 5 . 定义 max{ a , b } = 已知 函数 f ( x ) = max{ | 2 x- 1 | , ax 2 +b }, 其中 a< 0, b ∈ R , 若 f (0) =b , 则实数 b 的范围为 　　　　　 , 若 f ( x ) 的最小值为 1, 则 a+b= 　　　　　 .   [1, +∞ ) 　 1 解析 : ∵ f (0) = max{1, b } =b , ∴ b ≥ 1; 作出 y=| 2 x- 1 | 与 y=ax 2 +b 的函数图象 , 如图所示 : ∵ f ( x ) 的最小值为 1, ∴ y=ax 2 +b 恰好经过点 (1,1), ∴ a+b= 1 .