安徽省示范高中2018—2019学年高三上学期考试试题 理科数学(解析版) 14页

安徽省示范高中 2018—2019 学年高三上学期考试试题 理科数学 一、选择题：本题共 12 小题，每小题 5 分，共 60 分．在每小题给出的四个选项中，只有一项是符合题目 要求的． 1．已知集合 { | 0}, {1,2,3}A x x a B  ≤ ，若 A B   ，则 a 的取值范围为（ ） A．( ,1] B．[1, ) C．( ,3] D．[3, ) 1．答案：B 解析：集合 { | }A x x a ≤ ，集合 {1,2,3}B  ，若 A B   ，则 1，2，3 这三个元素至少有一个在集合 A 中，若 2 或 3 在集合 A 中，则 1 一定在集合 A 中，因此只要保证1 A 即可，所以 1a≥ ． 2． z 是 1 2i 1 iz   的共轭复数，则 z 的虚部为（ ） A． 1 2 B． 1 2 C． 3 2 D． 3 2 2．答案：C 解析： 1 2i (1 2i)(1 i) 1 3i 1 3 i1 i (1 i)(1 i) 2 2 2z             ，则 1 3 i2 2z    ，所以 z 的虚部为 3 2 ． 3．已知下列两个命题 1p ：存在正数 a ，使函数 2 2x xy a    在 R 上为偶函数； 2p ：函数 sin cos 2y x x   无零点． 则在命题 1 1 2 2 1 2 3 1 2 4 1 2: , : , : ( ) , : ( )q p p q p p q p p q p p      中，真命题是（ ） A． 1 4,q q B． 2 3,q q C． 1 3,q q D． 2 4,q q 3．答案：A 解析：当 1a  时， 2 2x xy a    在 R 上是偶函数，所以 1p 为真命题； 当 5 4x  时，函数 sin cos 2 0y x x    ，所以命题 2p 是假命题． 所以 1 2p p ， 1 2( )p p  是真命题，故选 A． 4．《九章算术》是我国古代的数学名著，书中把三角形的田称为“圭田”，把直角梯形的田称为“邪田”， 称底是“广”；称高是“正从”，“步”是丈量土地的单位．现有一邪田，广分别是十步和二十步，正从为 十步，其内有一块广为八步，正从为五步的圭田．若在邪田内随机种植一株茶树，求该茶树恰好种在圭田 内的概率为（ ） A． 2 15 B． 2 5 C． 4 15 D． 1 5 4．答案：A 解析：由题意可得邪田的面积 1 (10 20) 10 1502S      ，圭田的面积 1 1 8 5 202S     ， 则所求概率 1 20 2 150 15 SP S   ． 5．角 的顶点为坐标原点，始边为 x 轴正半轴，终边经过点 (4, )P y ，且 3sin 5   ，则 tan （ ） A． 4 3 B． 4 3 C． 3 4 D． 3 4 5．答案：C 解析：因为角 的终边经过点 (4, )P y ， 3sin 05    ，所以角 为第四象限角，所以 2 4cos 1 sin 5    ，所以 sin 3tan cos 4     ． 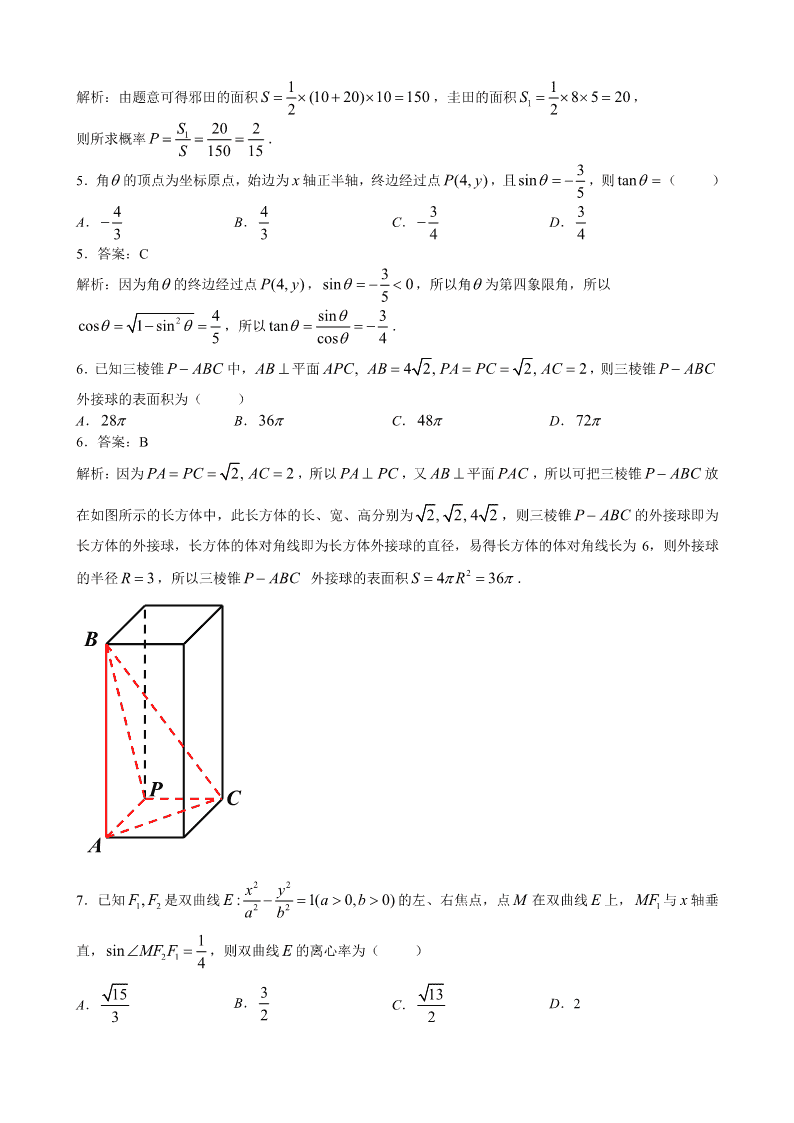6．已知三棱锥 P ABC 中，AB  平面 , 4 2, 2, 2APC AB PA PC AC    ，则三棱锥 P ABC 外接球的表面积为（ ） A． 28 B．36 C． 48 D．72 6．答案：B 解析：因为 2, 2PA PC AC   ，所以 PA PC ，又 AB  平面 PAC ，所以可把三棱锥 P ABC 放 在如图所示的长方体中，此长方体的长、宽、高分别为 2, 2, 4 2 ，则三棱锥 P ABC 的外接球即为 长方体的外接球，长方体的体对角线即为长方体外接球的直径，易得长方体的体对角线长为 6，则外接球 的半径 3R  ，所以三棱锥 P ABC 外接球的表面积 24 36S R   ． A P B C 7．已知 1 2,F F 是双曲线 2 2 2 2: 1( 0, 0)x yE a ba b    的左、右焦点，点 M 在双曲线 E 上， 1MF 与 x 轴垂 直， 2 1 1sin 4MF F  ，则双曲线 E 的离心率为（ ） A． 15 3 B． 3 2 C． 13 2 D．2 7．答案：A 解析：由题意知 1( ,0)F c ，因为 1MF 与 x 轴垂直，且 M 在椭圆上，所以 2 1 bMF a ．在 1 1Rt MF F△ 中， 2 1 1sin 4MF F  ，所以 1 2 1 1 2 1tan 15 MFMF F F F   ，即 2 2 1 2 2 15 b ba c ac  ，又 2 2 2b c a  ， 所以 2 215 15 2 0c a ac   ，两边同时除以 2a ，得 215 2 15 0e e   ， ( 5 3)( 3 5) 0e e    ，又 1e  ，所以 15 3e  ． 解法二： 1 2 1 2 1sin 4 MFMF F MF   ，不妨设 1 21, 4MF MF  ，则 1 2 15F F  ，离心率 1 2 2 1 2 15 2 3 F Fc ce a a MF MF    ． M F1 F2O 8．函数 1( ) ( 1) x x ef x x e   （其中e 为自然对数的底数）的图象大致为（ ） 8．答案：D 解析：函数 ( )f x 的定义域为{ | 0}x x  ， 1 1 1( ) ( )( 1) (1 ) ( 1) x x x x x x e e ef x f xx e x e x e              ，∴函数 ( )f x 为偶函数，排除 A，C； 当 x   时， 1 10, 11 x x e x e   ，所以 1 0( 1) x x e x e   ，排除 B，选 D． 9．在平面几何中，与三角形的三条边所在直线的距离相等的点有且只有四个．类似的，在立体几何中， 与正四面体的四个面所在平面距离相等的点（ ） A．有且只有一个 B．有且只有三个 C．有且只有四个 D．有且只有五个 9．答案：D 解析：正四面体 P ABC 的内切球的球心到四个面所在平面的距离相等，将正四面体 P ABC 延拓为正 四面体 P DEF ，所得三棱台 ABC DEF 内存在一个球，其球心到平面 PDE ，平面 PEF ，平面 PDF 的距离相等，同理，分别将四面体 , ,A PBC B PAC C PAB   进行延拓均可得到一个满足题意的点， 因此满足题意的点有且只有五个，故选 D． P A B C D E F O2 O3 O1 O A B C 10．已知函数 ( ) sin(2 ) ( 0, )2f x A x A      的部分图象如图所示， ( ) ( ) 0f a f b  ， ( ) 3f a b  ，则（ ） A． ( )f x 在 5 ,12 12      上是减函数 B． ( )f x 在 5 ,12 12      上是增函数 C． ( )f x 在 5,3 6       上是减函数 D． ( )f x 在 5,3 6       上是增函数 10．答案：B 解析：由图可知 2A  ，因为 ( ) ( ) 0f a f b  ，所以 22 a bf      ， 2a b     ， 3( ) 2sin(2 2 ) 3, sin(2 2 ) 2f a b a b a b          ， 22 2 3a b     ， 由 2 22 2 3 a b a b           ，解得 3   ， ( ) 2sin 2 3f x x       ， 当 5 ,12 12x       时， 2 ,3 2 2x         ，所以 ( )f x 在 5 ,12 12      上是增函数． 当 5,3 6x      时， 2 ( ,2 )3x     ，所以 ( )f x 在 5,3 6       上先减后增．故选 B． 11．设抛物线 2: 2 ( 0)C y px p  的焦点为 F ，点 M 在C 上， 5MF  ，若以 MF 为直径的圆过点 (0, 2) ， 则C 的焦点到准线的距离为（ ） A．4 或 8 B．2 或 4 C．2 或 8 D．4 或 16 11．答案：C 解析：如图，线段 MF 的中点 N 的纵坐标 2Ny  ，所以点 M 的纵坐标 4My  ， 8 Mx p  ， 则 8 52 2M p pMF x p     ， 2 10 16 0, ( 2)( 8) 0, 2p p p p p         或 8p  ． (0,2) N M O F 12．设函数 ( )f x 在 R 上存在导数 ( )f x ，对任意的 Rx ，有 ( ) ( ) 0f x f x   ，且 [0, )x  时， ( ) 2f x x  ．若 ( 2) ( ) 4 4f a f a a  ≥ ，则实数 a 的取值范围为 （ ） A．( ,1] B．[1, ) C．( ,2] D．[2, ) 12．答案：A 解析：设 2( ) ( )g x f x x  ， ( )f x 为偶函数， ( )g x 也是偶函数，当 [0, )x  时， ( ) ( ) 2 0g x f x x    ， ( )g x 在[0, ) 上单调递增， 由 2 2( 2) ( ) 4 4 ( 2)f a f a a a a     ≥ ，得 2 2( 2) ( 2) ( )f a a f a a   ≥ ，即 ( 2) ( )g a g a ≥ ， 2a a  ≥ ，即 2 24 4a a a  ≥ ，解得 1a ≤ ． 二、填空题：本题共 4 小题，每小题 5 分，共 20 分．把答案填在题中的横线上． 13．如图，在平行四边形 ABCD 中， ,E F 分别为边 ,AB BC 的中点，连接 ,CE DF ，交于点G ． 若 ( , )RCG CD CB         ，则    ． A B CD E F G 13．答案： 1 2 解析：由题图可设 ( 0)CG xCE x    ，则   1 2 2 xCG x CB BE x CB CD CD xCB                ，因为 CG CD CB      ，CD  与CB  不共线，所以 ,2 x x   ，所以 1 2    解法二：特值法，不妨设平行四边形 ABCD 是边长为 2 的正方形，则 (2,2), (0, 2), (2,1), (1,0)C D F E ， (2,0)B ，直线 DF 的方程为 2 4 0x y   ，直线CE 的方程为 2 2 0x y   ， 联立 8 2 4 0 5 2 2 0 6 5 xx y x y y           ，即 8 6,5 5G     ， 2 4, , ( 2,0), (0, 2)5 5CG CD CF              ，由 CG CD CB      ，得 2 12 15 5 ,4 2 225 5                       ． A B CD E F G x y 14．设 ,x y 满足约束条件 7 0 3 1 0 3 5 0 x y x y x y         ≤ ≤ ≥ ，则 2z x y  的最小值为 ． 14．答案：2 解析：作可行域为如图所示的 ABC△ ，其中 (3, 4), (2,1), (5,2)A B C ，则 2, 3, 8A B Cz z z   ， min 2Az z   ． 5 4 3 2 1 2 4 6 C B A O 15．现有 16 张不同的卡片，其中红色、黄色、蓝色、绿色卡片各 4 张．从中任取 3 张，要求这 3 张卡片 不能是同一种颜色， 且红色卡片至多 1 张，不同取法的种数为 ． 15．答案：472 解析：解法一：从 16 张不同的卡片中任取 3 张，不同取法的种数为 3 16C ，其中有两张红色卡片的不同取法 的种数为 3 1 4 12C C ，其中三张卡片颜色相同的不同取法的种数为 3 1 4 4C C ，所以 3 张卡片不能是同一种颜 色， 且红色卡片至多 1 张的不同取法的种数为 3 3 1 3 1 16 4 12 4 4 472C C C C C     ． 解法二：分两类： ①若没有红色卡片，则需从黄、蓝、绿三种颜色的卡片中选 3 张，若都是不同色，则不同取法的种数为 4 4 4 64   ，若 2 张颜色相同，则不同的取法的种数为 2 1 2 1 3 2 4 4 144C C C C    ． ②若红色卡片有 1 张，则剩余 2 张不同色时，不同取法的种数为 1 2 1 1 4 3 4 4 192C C C C    ， 剩余 2 张同色时，不同取法的种数为 1 1 2 4 3 4 72C C C   ． 所以不同的取法共有64 144 192 72 472    （种）． 16．在 ABC△ 中， 90ABC  ，延长 AC 到 D ，使得 1CD AB  ，若 30CBD  ，则 AC  ． 16．答案： 3 2 解析：设 ( 0)AC x x  ，在 BCD△ 中，由正弦定理得 sin sin BD CD BCD CBD  ，所以 2sinBD BCD  ， 又 1sin sinBCD ACB x    ，所以 2BD x ． 在 ABD△ 中， 120ABD   ，由余弦定理可得： 2 2 2 2 cos120AD AB BD AB BD     ， 即 2 2 4 2( 1) 1 2 cos120x x x      ，整理得： 2 3 3 2 2 42 , ( 2) 2( 2), 2xx x x x x xx        ， 故 3 2x  ，故 3 2AC  ． D C A B 三、解答题：共 70 分．解答应写出文字说明、证明过程或演算步骤．第 17~21 题为必考题，每个试题考 生都必须作答．第 22、23 题为选考题，考生根据要求作答． （一）必考题：共 60 分． 17．（本小题满分 12 分） 设数列{ }na 的前 n 项和为 nS ，且满足 2n nS a  ， 1,2,3,n  ．数列{ }nb 满足 1 1b  ，且 1n n nb b a   ． （1）求数列{ }nb 的通项公式； （2）设 (3 )n nc n b  ，数列{ }nc 的前 n 项和为 nT ，求 nT ． 17．解析：（1）当 1n  时， 1 1 1 1 12 , 2 , 1S a a a a       ． 由 2n nS a  ① ，可得 1 12n nS a   ② ， ① ② ，得 1n n na a a    ，即 1 1 ( 2)2n na a n ≥ ， 所以数列{ }na 是首项为 1，公比为 1 2 的等比数列， 1 1 2n na   ． 由 1n n nb b a   ，得 1 1 1 2n n nb b   ，得 1 2 1 ( 2)2n n nb b n   ≥ ， 1 1 2 2 1 1 2 3 2 1 1 1( ) ( ) ( ) 1 1 32 2 2n n n n n n n nb b b b b b b b                      ， 又 1 1b  也符合上式， 2 13 ( )2n nb n     N ．………………………………………………6 分 解法二： 1 11 1 2 1 1 2 1 2 1 1 1 1 1,2 2 2 2 2 2n n n nn n n n n nb b b b                ， 数列 2 1 2n nb      是常数列，首项为 1 1 2 1 1 2 32b     ，所以 2 2 1 13, 3 ( )2 2n nn nb b n        N （2） 2 1(3 ) 2n n nc n b n     ， 3 2 2 1 1 1 11 2 2 1 3 ( 1)2 2 2 1 1 1 1 11 1 2 3 ( 1)2 2 4 2 2 n n n n n n T n n T n n                                ① ② 两式相减，得 2 1 2 1 1 1 1 1 1 1 1 1 22 1 4 42 2 4 2 2 2 2 2n n n n n n nT n n                   ， 2 28 2n n nT     ．……………………………………………………………………………………12 分 18．（本小题满分 12 分） 如图，三棱柱 ABC A B C   的棱长均为 2，O 为 AC 的中点，平面 A OB  平面 ABC ，平面 AA C C   平面 ABC ． （1）求证： A O  平面 ABC ； （2）求二面角 A BB C    的余弦值． A B C O A B C 18．解析：（1）在等边三角形 ABC 中，O 为 AC 的中点，所以OB AC ． 因为平面 A OB  平面 ABC ，平面 A OB  平面 ABC OB ， AC  平面 ABC ， AC OB ， AC  平面 A OB ，而 A O  平面 A OB ， AC A O  ；……………………………………2 分 因为平面 AA C C   平面 ABC ，平面 AA C C   平面 ABC AC ，OB  平面 ABC ，OB AC ， OB  平面 AA C C  ，而 A O  平面 AA C C  ， OB A O  ， AC OB O  ， A O  平面 ABC ．…………………………………………………………4 分 （2）由（1）知， A O  平面 ABC ，OB OC ，以 , ,OB OC OA 所在直线分别为 , ,x y z 轴建立如图所 示空间直角坐标系．则 (0, 1,0), (0,1,0), ( 3,0,0), (0,0, 3)A C B A ， 则 ( 3,1,0), (0,1, 3), ( 3,1,0)AB BB AA BC          ．………………………………6 分 设平面 AA B B  的法向量为 1 1 1( , , )m x y z  ， 则 1 1 1 1 3 0 3 0 m AB x y m BB y z              ，取 1 1x  ，则 1 13, 1, (1, 3,1)y z m      ．………………8 分 设平面 BB C C  的法向量为 2 2 2( , , )n x y z ， 则 2 2 2 2 3 0 3 0 n BC x y n BB y z               ，取 2 1x  ，则 2 23, 1, (1, 3, 1)y z n      ．………………10 分 所以 3 3cos , 55 5 m nm n m n            ， 又二面角 A BB C    为锐角，所以其余弦值为 3 5 ．…………………………………………12 分 A B C O A B C x y z 19．（本小题满分 12 分） 已知椭圆 2 2 2 2: 1( 0)x yC a ba b    的上顶点为 P ，右顶点为 Q ，直线 PQ 与圆 2 2 4 5x y  相切于点 2 4,5 5M      ． （1）求椭圆C 的方程； （2）若不经过点 P 的直线l 与椭圆C 交于 ,A B 两点，且 0PA PB    ，求证：直线l 过定点． 19．解析：（1）由已知得直线OM（O 为坐标原点）的斜率 2OMk  ，则直线 PQ 的斜率 1 1 2PQ OM k k    ， 所以直线 PQ 的方程为 4 1 2 5 2 5y x       ，即 2 2x y  ．…………………………………………2 分 可求得 (0,1), (2,0)P Q ，故 2, 1a b  ，故椭圆C 的方程为 2 2 14 x y  ．…………………………4 分 （2）当直线l 的斜率不存在时，显然不满足条件． 当直线l 的斜率存在时，设l 的方程为 ( 1)y kx n n   ， 由 2 2 14 x y y kx n       ，消去 y 并整理得 2 2 2(4 1) 8 4( 1) 0k x knx n     ， 2 2 2 2 2(8 ) 4 4(4 1)( 1) 16(4 1 ) 0kn k n k n          ，得 2 24 1k n  ． ① 设 1 1 2 2( , ), ( , )A x y B x y ，则 2 1 2 1 22 2 8 4( 1),4 1 4 1 kn nx x x xk k      ． ② 由 0PA PB    ，得 1 1 2 2( , 1) ( , 1) 0x y x y    ，又 1 1 2 2,y kx n y kx n    ， 所以 2 2 1 2 1 2( 1) ( 1)( ) ( 1) 0k x x k n x x n       ， ③ ………………8 分 将②代入③，得 2 2 2 2 2 2 4( 1)( 1) 8 ( 1) ( 1) 04 1 4 1 k n k n n nk k        ， ( 1)(5 3) 0n n    ， 解得 1n  （舍），或 3 5n   ，满足①． …………………………………………………10 分 此时l 的方程为 3 5y kx  ，故直线l 过定点 30, 5     ．………………………………………………12 分 20．（本小题满分 12 分） 前不久，安徽省社科院发布了 2017 年度“安徽城市居民幸福排行榜”，铜陵市成为本年度安徽“最幸福城 市” ．随后，师大附中学生会组织部分同学，用“10 分制”随机调查“阳光”社区人们的幸福度．现从 调查人群中随机抽取 16 名，如图所示的茎叶图（以小数点前的一位数字为茎，小数点后的一位数字为叶） 记录了他们的幸福度分数． 7 3 0 8 6 6 6 6 7 7 8 8 9 9 9 7 6 5 5 （1）指出这组数据的众数和中位数； （2）若幸福度不低于 9.5 分，则称该人的幸福度为“极幸福”，若从这 16 人中随机选取 3 人，至多有 1 人 的幸福度是“极幸福”的概率； （3）以这 16 人的样本数据来估计整个社区的总体数据，若从该社区（人数很多）任选 3 人，记 表示选 到幸福度为“极幸福”的人数，求 的分布列及数学期望． 20．解析：（1）由茎叶图得 8.6 出现的次数最多，所以众数为 8.6；将茎叶图中的所有数据从小到大排列， 得中位数为 8.75．…………………………………………………………………………………………2 分 （2）设事件 ( 1,2,3)iA i  表示所取 3 人中有i 人的幸福度是“极幸福”，至多有 1 人的幸福度是“极幸福” 记为事件 A ，结合茎叶图得 3 1 2 12 4 12 0 1 3 3 16 16 121( ) ( ) ( ) 140 C C CP A P A P A C C     ．…………………………6 分 （3） 的所有可能取值为 0，1，2，3，由样本估计总体中任选 1 人，其幸福度为“极幸福”的概率为 4 1 16 4 ， 则 3 2 1 3 2 3 2 3 3 27 1 3 27( 0) ; ( 1) ;4 64 4 4 64 1 3 9 1 1( 2) ; ( 3) .4 4 64 4 64 P P C P C P                                       所以 的分布列为：  0 1 2 3 P 27 64 27 64 9 64 1 64 所以 27 27 9 10 1 2 3 0.7564 64 64 64E          ．…………………………………………12 分 21．（本小题满分 12 分） 已知函数 ( ) 2 (ln 1)f x x x  ． （1）求函数 ( )f x 的单调区间； （2）若斜率为 k 的直线与曲线 ( )y f x 交于 1 1 2 2( , ), ( , )A x y B x y 两点，其中 1 2x x ，求证： 1 2 2x xk  ． 21．解析：（1） ( )f x 的定义域是 (0, ) ， ( ) 2ln 4f x x   ．………………………………2 分 令 ( ) 0f x  ，得 2x e ，…………………………………………………………………………3 分 当 2(0, )x e 时， ( ) 0f x  ，此时 ( )f x 单调递减； 当 2( , )x e  时， ( ) 0f x  ，此时 ( )f x 单调递增． 所以 ( )f x 的单调递减区间为 2(0, )e ，单调递增区间为 2( , )e  ．………………………………5 分 （2） 2 1 2 1 2 1 2 1 ( ) ( ) 2ln 2lnf x f x x xk x x x x      ．………………………………………………………6 分 要证 1 2 2x xk  ，即证 2 1 1 2 2 1ln ln x xx xx x   ，……………………………………………………7 分 即证 2 1 2 2 1 1 1 1 ln x x x x x x    ．………………………………………………………………………………8 分 令 2 1 xt x （由 1 2x x ，知 1t  ），……………………………………………………………………9 分 则只需证ln 1 ln ( 1)t t t t t    ．（*）………………………………………………………………10 分 ①设 ( ) 1 lng t t t   ，则当 1t  时， 1( ) 1 0g t t     ，所以 ( )g t 在 (1, ) 上是增函数， 当 1t  时， ( ) 1 ln (1) 0g t t t h     ，即 1 lnt t  ； ②设 ( ) ln ( 1)h t t t t   ，则当 1t  时， ( ) ln 0h t t   ，所以 ( )h t 在 (1, ) 上是增函数， 当 1t  时， ( ) ln ( 1) (1) 0h t t t t h     ，即 ln 1t t t  ． 由①②知（*）成立，所以 1 2 2x xk  ．………………………………………………………………12 分 （二）选考题：共 10 分．请考生在第 22、23 题中任选一题作答．如果多做，则按所作的第一题计分． 22．【选修 4—4：坐标系与参数方程】（本小题满分 10 分） 在直角坐标系 xOy 中，直线 1 : 0l x  ，圆 2 2: ( 1) ( 1 2) 1C x y     ，以坐标原点为极点，x 轴的正半 轴为极轴建立极坐标系． （1）求直线 1l 和圆C 的极坐标方程； （2）若直线 2l 的极坐标方程为 ( )4   R ，设 1 2,l l 与圆C 的公共点分别为 ,A B ，求 OAB△ 的面积． 22．解析：（1） cos , sinx y     ， 直线 1l 的极坐标方程为 cos 0   ，即 ( )2   R ， 圆C 的极坐标方程为 2 2 cos 2(1 2) sin 3 2 2 0          ．…………………………5 分 （2）设 1 2, , ,2 4A B             ，将 2   代入 2 2 cos 2(1 2) sin 3 2 2 0          ， 得 2 2(1 2) 3 2 2 0      ，解得 1 1 2   ． 将 4   代入 2 2 cos 2(1 2) sin 3 2 2 0          ， 得 2 2(1 2) 3 2 2 0      ，解得 2 1 2   ． 故 OAB△ 的面积为 21 3 2(1 2) sin 12 4 4      ．……………………………………10 分 23．【选修 4—5：不等式选讲】（本小题满分 10 分） 已知 ( ) 2f x x  ． （1）解不等式 ( ) 1 (2 )f x f x  ； （2）若 ( ) 1, (2 ) 2f m f n≤ ≤ ，求 2 1m n  的最大值，并求此时实数 ,m n 的取值． 23．解析：（1）原不等式等价于 2 1 2 1x x    ， 1 2 1 2 2 x x x      或 1 2 2 1 2 2 x x x       ≤ ≤ 或 2 2 1 2 2 x x x       ，………………………………2 分 1 1x   或 51 3x ≤ 或 ，∴原不等式的解集为 51, 3     ．……………………………………5 分 （2）由题意得 ( ) 2 1, (2 ) 2 2 2, 1 1f m m f n n n     ≤ ≤ ≤ ，…………………………6 分 2 1 ( 2) 2( 1) 1 2 2 1 1 4m n m n m n           ≤ ≤ ， 当且仅当 1, 2m n  时， 2 1m n  取得最大值 4．…………………………………………10 分