2018-2019学年河北省正定县第三中学高二10月月考数学试题 Word版 7页

‎ 2018-2019学年河北省正定县第三中学高二10月月考数学试卷 一、选择题（本题共12道小题，每小题5分）‎ ‎1.已知圆x2+y2﹣2x+6y=0，则该圆的圆心及半径分别为（　　）‎ A．（1，﹣3），﹣10 B．（1，﹣3）， ‎ C．（1，3），﹣10 D．（1，3），﹣‎ ‎2.圆心为（1，1）且过原点的圆的方程是（　　）‎ A．（x﹣1）2+（y﹣1）2=1 B．（x+1）2+（y+1）2=1‎ C．（x+1）2+（y+1）2=2 D．（x﹣1）2+（y﹣1）2=2‎ ‎3.圆和圆的位置关系为( ).‎ A.相离 B.相交 C.外切 D.内含 ‎4.圆（x﹣2）2+y2=2上的点与点A（﹣1，3）的距离的最大值为（　　）‎ A． B． C． D．‎ ‎5.有50件产品，编号从1到50，现在从中抽取5件检验，用系统抽样确定所抽取的第一个样本编号为7，则第三个样本编号是 A. 37 B. 27 C. 17 D. 12‎ ‎6.某工厂生产A、B、C三种不同型号的产品，其数量之比依次是3：4：7，现在用分层抽样的方法抽出样本容量为n的样本，样本中A型号产品有15件，那么n等于（　　）A．50 B．60 C．70 D．80‎ 一年级 二年级 三年级 女生 ‎373‎ x y 男生 ‎377‎ ‎370‎ z ‎7.某校共有学生2000名，各年级男、女生人数如表．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19．现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为（　　）‎ A．24 B．18 ‎ C．16 D．12‎ ‎8.从500件产品中随机抽取20件进行抽样，利用随机数表法抽取样本时，先将这500件产品按001，002，003，…，500进行编号，如果从随机数表的第1行第6列开始，从左往右依次选取三个数字，则选出来的第4个个体编号为（　　）‎ ‎1622 7794 3949 5443 5482 1737 9323 7887 3520 9643‎ ‎8626 3491 6484 4217 5331 5724 5506 8877 0474 4767．‎ A．435 B．482 C．173 D．237‎ ‎9.以下茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩（单位：分）．已知甲组数据的中位数为15，乙组数据的平均数为16.8，则x，y的值分别为（　　）‎ ‎ A．2，5 B．5，5 C．5，8 D．8，8‎ ‎10.已知的取值如表所示，从散点图分析与的线性关系，且，则 x ‎0‎ ‎1‎ ‎3‎ ‎4‎ y ‎2.2‎ ‎4.3‎ ‎4.8‎ ‎6.7‎ A．2.2 B．3. 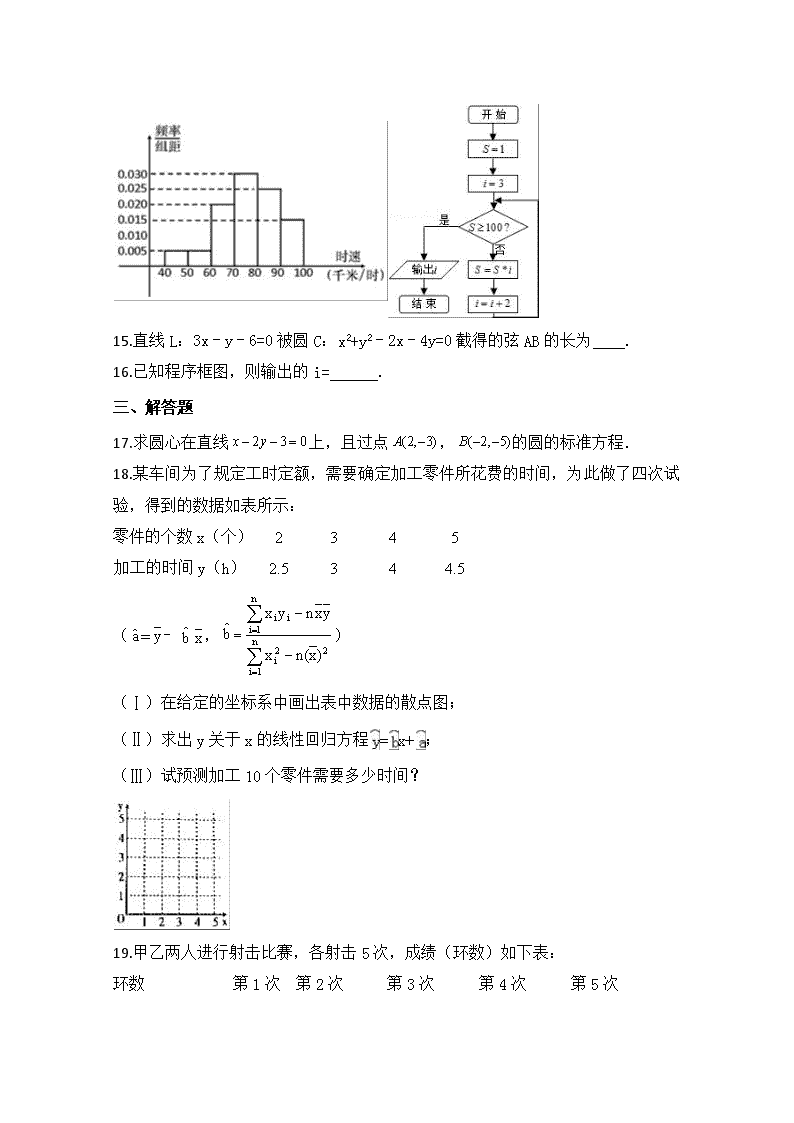36 C．2.6 D．1.95‎ ‎11.福建省第十六届运动会将于2018年在宁德召开，组委会预备在会议期间从3女2男共5名志愿者中任选2名志愿者参考接待工作，则选到的都是女性志愿者的概率为（ ）‎ A． B． C． D． ‎ ‎12.袋中装有红球3个、白球2个、黑球1个，从中任取2个，则互斥而不对立的两个事件是（　　）‎ A．至少有一个白球；至少有一个红球 B．至少有一个白球；红、黑球各一个 C．恰有一个白球；一个白球一个黑球 D．至少有一个白球；都是白球 二、填空题（本题共4道小题，每小题5分）‎ ‎13.已知点A（-4，-5），B（6，-1），则以线段AB为直径的圆的方程________________‎ ‎14.如图为某天通过204国道某测速点的汽车时速频率分布直方图，则通过该测速点的300辆汽车中时速在[60，80）的汽车大约有　　辆．‎ ‎15.直线L：3x﹣y﹣6=0被圆C：x2+y2﹣2x﹣4y=0截得的弦AB的长为　　．‎ ‎16.已知程序框图，则输出的i=　 　．‎ 三、解答题 ‎17.求圆心在直线上，且过点，的圆的标准方程．‎ ‎18.某车间为了规定工时定额，需要确定加工零件所花费的时间，为此做了四次试验，得到的数据如表所示：‎ 零件的个数x（个）‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 加工的时间y（h）‎ ‎2.5‎ ‎3‎ ‎4‎ ‎4.5‎ ‎（=﹣，）‎ ‎（Ⅰ）在给定的坐标系中画出表中数据的散点图；‎ ‎（Ⅱ）求出y关于x的线性回归方程=x+；‎ ‎（Ⅲ）试预测加工10个零件需要多少时间？‎ ‎19.甲乙两人进行射击比赛，各射击5次，成绩（环数）如下表：‎ 环数 第1次 第2次 第3次 第4次 第5次 甲 ‎4‎ ‎5‎ ‎7‎ ‎9‎ ‎10‎ 乙 ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎（1）分别求出甲、乙射击成绩的平均数及方差，并由此分析两人的射击水平；‎ ‎（2）若分别对甲、乙两人各取一次成绩，求两人成绩之差不超过2环的概率．‎ ‎20.某企业员工共500人参加“学雷锋”志愿活动，按年龄分组：第一组[25，30），第2组[30，35），第3组[35，40），第4组[40，45），第5组[45，50]，得到的频率分布直方图如图所示．‎ 区间 ‎[25，30）‎ ‎[30，35）‎ ‎[35，40）‎ ‎[40，45）‎ ‎[45，50]‎ 人数 ‎50‎ ‎50‎ a ‎150‎ b ‎（1）表是年龄的频数分布表，求正整数a，b的值；‎ ‎（2）根据频率分布直方图，估算该企业员工的平均年龄及年龄的中位数；‎ ‎（3）现在要从年龄较小的第1，2，3组中用分层抽样的方法抽取6人，从这6人中随机抽取2人参加社区宣传交流活动，求至少有1人年龄在第3组的概率．‎ 数学答案：‎ 一、选择题：1—12 BDBBB CCCCC BB 二、填空题 ‎13． 14. 150‎ ‎15. 16. 9‎ 三、解答题 ‎17.‎ 解：∵，‎ 中点，‎ ‎∴中垂线为，‎ 整理得，‎ 联立，‎ 解出，，‎ ‎∴圆心为，‎ 半径为，圆为．‎ ‎18. 解：（Ⅰ）散点图如图所示，‎ ‎ ‎ ‎（Ⅱ）由表中数据得： xiyi=52.5， xi2=54， =3.5， =3.5，‎ ‎∴b==0.7，‎ ‎∴a=3.5﹣0.7×3.5=1.05，‎ ‎∴y=0.7x+1.05．‎ ‎（Ⅲ）将x=10代入回归直线方程，‎ y=0.7×10+1.05=8.05（小时）．‎ ‎∴预测加工10个零件需要8.05小时．‎ ‎19.‎ 解：（1）依题中的数据可得：‎ ‎=（4+5+7+9+10）=7，‎ ‎=（5+6+7+8+9）=7…‎ ‎= [（4﹣7）2+（5﹣7）2+（7﹣7）2+（9﹣7）2+（10﹣7）2]=5.2‎ ‎= [（5﹣7）2+（6﹣7）2+（7﹣7）2+（8﹣7）2+（9﹣7）2]=2…‎ ‎∵=，＞‎ ‎∴两人的总体水平相同，甲的稳定性比乙差…‎ ‎（2）设事件A表示：两人成绩之差不超过2环，‎ 对甲、乙两人各取一次成绩包含的基本事件为 ‎（4，5），（4，6），（4，7），（4，8），（4，9）‎ ‎（5，5），（5，6），（5，7），（5，8），（5，9）‎ ‎（7，5），（7，6），（7，7），（7，8），（7，9）‎ ‎（9，5），（9，6），（9，7），（9，8），（9，9）‎ ‎（10，5），（10，6），（10，7），（10，8），（10，9）共25种 事件A包含的基本事件为：‎ ‎（4，5）（4，6），（5，5），（5，6），（5，7）‎ ‎（7，5）（7，6），（7，7），（7，8），（7，9）‎ ‎（9，7），（9，8），（9，9），（10，8），（10，9）共15种 ‎∴P（A）==…‎ ‎20. 解：（Ⅰ）由题设可知，a=0.08×5×500=200，b=0.02×5×500=50，‎ ‎（Ⅱ）根据频率分布直方图可得，平均年龄为=（ 27.5×0.02+32.5×0.02+37.5×0.08+42.5×0.06+47.5×0.02）×5=38.5，‎ 估计中位数为：35+=35.75，‎ ‎（III）因为第1，2，3组共有50+50+200=300人，‎ 利用分层抽样在300名学生中抽取6名学生，每组抽取的人数分别为：‎ 第1组的人数为6×=1‎ 第2组的人数为6×=1‎ 第3组的人数为=4 ‎ 设第1组的1位同学为A，第2组的1位同学为B，第3组的4位同学为C1，C2，C3，C4，‎ 则从六位同学中抽两位同学有：（A，B），（A，C1），（A，C2），（A，C3），（A，C4），（B，C1），（B，C2），（B，C3），（B，C4），（C1，C2），（C1，C3），（C1，C4），（C2，C3），（C2，C4），（C3，C4），共15种可能．‎ 其中2人年龄都不在第3组的有：（A，B），共1种可能，‎ 所以至少有1人年龄在第3组的概率为1﹣．‎