2021高考数学一轮复习课后限时集训64模拟方法--概率的应用文北师大版2 6页

课后限时集训64‎ 模拟方法——概率的应用 建议用时：45分钟 一、选择题 ‎1．(2016·全国卷Ⅱ)某路口人行横道的信号灯为红灯和绿灯交替出现，红灯持续时间为40秒．若一名行人来到该路口遇到红灯，则至少需要等待15秒才出现绿灯的概率为(　　)‎ A.　　　B.　　　C.　　　D. B　[如图，若该行人在时间段AB的某一时刻来到该路口，则该行人至少等待15秒才出现绿灯．AB长度为40－15＝25，由几何概型的概率公式知，至少需要等待15秒才出现绿灯的概率为＝，故选B.]‎ ‎2．在区间[0，π]上随机地取一个数x，则事件“sin x≤”发生的概率为(　　)‎ A. B. ‎ C. D. D　[x∈∪时，sin x≤，故概率为＝.]‎ ‎3．已知函数f(x)＝x2－x－2，x∈[－3,3]，在定义域内任取一点x0，使f(x0)≤0的概率是(　　)‎ A. B. ‎ C. D. 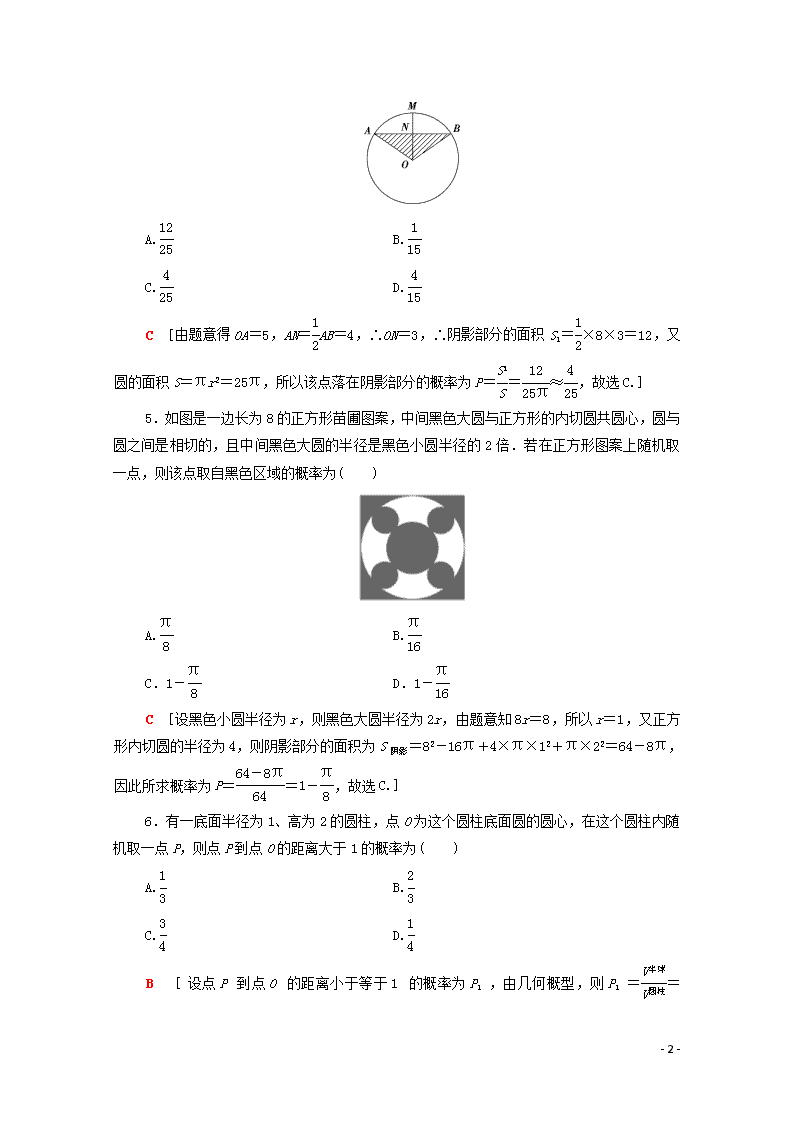C　[由f(x0)≤0可得－1≤x0≤2，所以D＝3－(－3)＝6，d＝2－(－1)＝3，故由几何概型的计算公式可得所求概率为P＝＝，故选C.]‎ ‎4．如图，圆O的半径为5，弦AB的长为8，OM⊥AB，交AB于点N，向圆O内随机投入一点，若圆周率π按3计算，则该点恰好落在阴影部分的概率约为(　　)‎ - 6 -‎ A. B. ‎ C. D. C　[由题意得OA＝5，AN＝AB＝4，∴ON＝3，∴阴影部分的面积S1＝×8×3＝12，又圆的面积S＝πr2＝25π，所以该点落在阴影部分的概率为P＝＝≈，故选C.]‎ ‎5．如图是一边长为8的正方形苗圃图案，中间黑色大圆与正方形的内切圆共圆心，圆与圆之间是相切的，且中间黑色大圆的半径是黑色小圆半径的2倍．若在正方形图案上随机取一点，则该点取自黑色区域的概率为(　　)‎ A. B. C．1－ D．1－ C　[设黑色小圆半径为r，则黑色大圆半径为2r，由题意知8r＝8，所以r＝1，又正方形内切圆的半径为4，则阴影部分的面积为S阴影＝82－16π＋4×π×12＋π×22＝64－8π，因此所求概率为P＝＝1－，故选C.]‎ ‎6．有一底面半径为1、高为2的圆柱，点O为这个圆柱底面圆的圆心，在这个圆柱内随机取一点P，则点P到点O的距离大于1的概率为(　　)‎ A. B. ‎ C. D. B　[设点P到点O的距离小于等于1的概率为P1，由几何概型，则P1＝＝＝.‎ 故点P到点O的距离大于1的概率P＝1－＝.]‎ ‎7．在平面区域{(x，y)|0≤x≤1,1≤y≤2}内随机投入一点P，则点P的坐标(x，y)满足y≤2x的概率为(　　)‎ - 6 -‎ A. B. ‎ C. D. A　[依题意作出图像如图，则P(y≤2x)＝＝＝.]‎ 二、填空题 ‎8．在区间[－3,5]上随机取一个实数a，则使函数f(x)＝x2＋4x＋a无零点的概率为________．‎ 　[∵函数f(x)＝x2＋4x＋a无零点，∴Δ＝42－4a＜0，即a＞4.即a∈(4,5)，区间长度为1.∵在区间[－3,5]上随机取一个实数a，且区间[－3,5]的长度为8，∴所求事件的概率为.]‎ ‎9．一只蜜蜂在一个半径为3的球O内自由飞行，若蜜蜂在飞行过程中始终保持与球的表面的距离大于1，称其为“安全飞行”，则蜜蜂“安全飞行”的概率为________．‎ 　[由题意得蜜蜂“安全飞行”的空间是以O为球心，2为半径的球，则由几何概型的概率公式，得蜜蜂“安全飞行”的概率P＝＝.]‎ ‎10．已知等腰Rt△ABC中，∠C＝90°，在∠CAB内作射线AM，则使∠CAM＜30°的概率为________．‎ 　[如图，在∠CAB内作射线AM0，使∠CAM0＝30°，于是有P(∠CAM＜30°)＝＝＝.‎ ‎]‎ - 6 -‎ ‎1．(2019·济南模拟)如图，在△ABC中，∠C＝90°，BC＝2，AC＝3，三角形内的空白部分由三个半径均为1的扇形构成，向△ABC内随机投掷一点，则该点落在阴影部分的概率为(　　)‎ A.　　　　　 B．1－ C. D．1－ B　[SRt△ABC＝×2×3＝3，S空白＝×π×12＝，所求概率P＝1－＝1－，故选B.]‎ ‎2．在面积为S的平行四边形ABCD内任取一点P，则△PBD的面积大于的概率为(　　)‎ A.　　　B. C.　　　D. A　[如图，平行四边形ABCD的面积为S，则△BCD的面积为，当△PBD的面积大于时，＝，则＝.∴＝.∴在面积为S的平行四边形ABCD内任取一点P，则△PBD的面积大于的概率为，故选A.]‎ ‎3．已知以原点O为圆心，1为半径的圆以及函数y＝x3的图像如图所示，则向圆内任意投掷一粒小米(视为质点)，该小米落入阴影部分的概率为________．‎ 　[由图形的对称性知，S阴影＝S圆，‎ 从而所求概率P＝＝.]‎ ‎4．(2019·宁乡模拟)函数f(x)＝，且a∈[0,1]，b∈(1,2]，则满足f(a)≥f(b - 6 -‎ ‎)的概率是________．‎ 　[依题意，所有试验结果构成的区域为a∈[0,1]，b∈(1,2]的正方形区域，面积为1，满足f(a)≥f(b)的区域即满足a2＋(b－1)2≤1的区域为以(0,1)为圆心，以1为半径的圆与正方形的公共区域，即为个圆，所以满足f(a)≥f(b)的概率是：P＝＝＝.‎ ‎]‎ ‎1．若a∈[1,6]，则函数y＝在区间[2，＋∞)上单调递增的概率是(　　)‎ A.　　　　B.　　　　C.　　　　D. C　[因为函数y＝＝x＋在区间(0，)上单调递减，在区间(，＋∞)上单调递增，而1≤a≤6，所以1≤≤.要使函数y＝在区间[2，＋∞)上单调递增，则≤2，即1≤a≤4，所以P(1≤a≤4)＝＝.故选C.]‎ ‎2．某校早上8：00开始上课，假设该校学生小张与小王在早上7：30～7：50之间到校，且每人在该时间段的任何时刻到校是等可能的，则小张比小王至少早5分钟到校的概率为________．(用数字作答)．‎ 　[设小张到校的时间为x，小王到校的时间为y，(x，y)可以看成平面中的点，试验的全部结果所构成的区域为Ω＝{(x，y)|30≤x≤50,30≤y≤50}是一个矩形区域，对应的面积S＝20×20＝400，‎ 则小张比小王至少早5分钟到校为事件A＝{x|y－x≥5}，作出符合题意的图像，则符合题意的区域为△ABC，‎ - 6 -‎ 联立得C(45,50)，联立得B(30,35)，则S△ABC＝×15×15，由几何概率模型可知小张比小王至少早5分钟到校的概率为＝.]‎ - 6 -‎