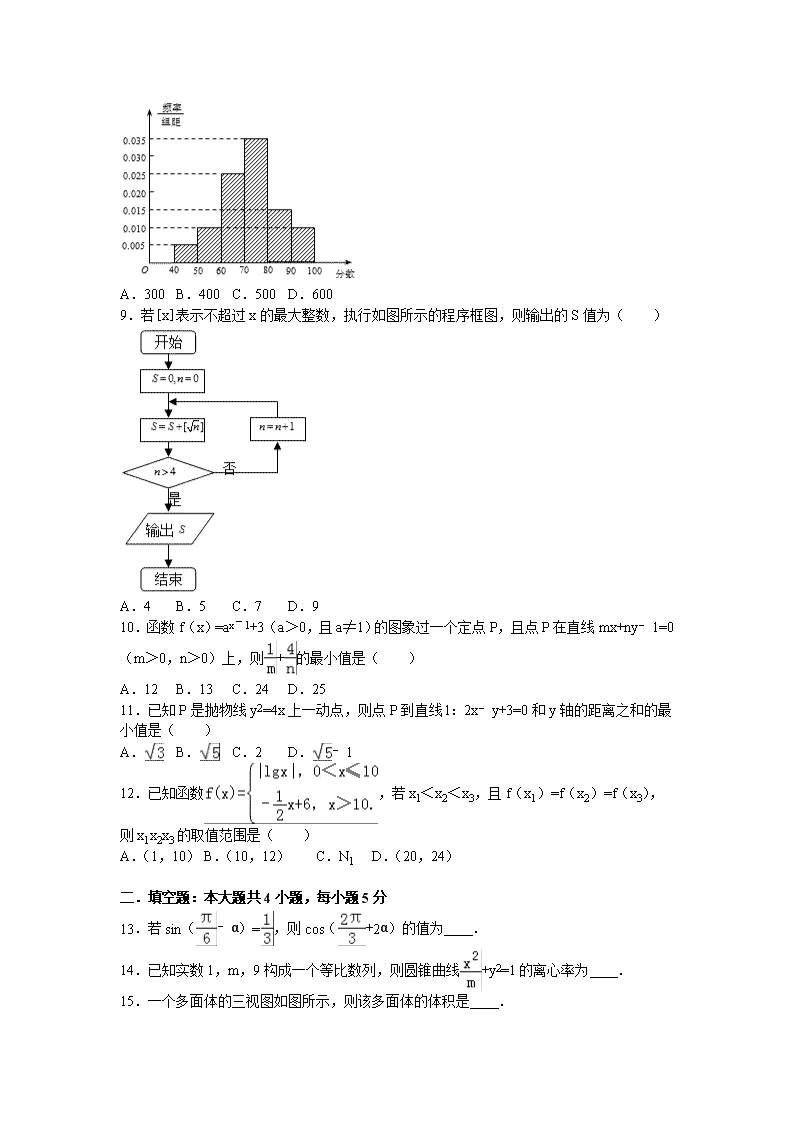数学卷·2018届辽宁省大连市瓦房店高中高二上学期期中数学试卷（文科） （解析版） 17页

‎2016-2017学年辽宁省大连市瓦房店高中高二（上）期中数学试卷（文科）‎ ‎　‎ 一．选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．设全集U={1，2，3，4，5}，集合A={1，2}，B={2，3，5}，则（∁UA）∪B=（　　）‎ A．{3，5} B．{3，4，5} C．{2，3，4，5} D．{1，2，3，4}‎ ‎2．已知向量=（﹣3，4），=（1，m），若⊥（﹣），m=（　　）‎ A． B．7 C．﹣7 D．﹣‎ ‎3．某高级中学有高一、二、三三个年级的学生共1600名，其中高三学生400名，如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本，则应从高三年级学生中抽取的人数是（　　）‎ A．40 B．30 C．20 D．10‎ ‎4．北宋 欧阳修在《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆其扣，徐以杓酌油沥之，自钱孔入，而钱不湿．因曰：‘我亦无他，唯手熟尔．’”可见技能都能透过反复苦练而达至熟能生巧之境的．若铜钱是半径为1cm的圆，中间有边长为0.5cm的正方形孔，你随机向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率为（　　）‎ A． B． C． D．‎ ‎5．直线x﹣y+3=0被圆（x+2）2+（y﹣2）2=2截得的弦长等于（　　）‎ A． B． C．2 D．‎ ‎6．某公司为确定明年投入某产品的广告支出，对近5年的广告支出m与销售额y（单位：百万元）进行了初步统计，得到下列表格中的数据：‎ y ‎30‎ ‎40‎ p ‎50‎ ‎70‎ m ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 经测算，年广告支出m与年销售额y满足线性回归方程=6.5m+17.5，则p的值为（　　）‎ A．45 B．50 C．55 D．60‎ ‎7．下列结论正确的是（　　）‎ A．“x≠1”是“x2≠1”的充分不必要条件 B．若“p∧q”与“¬p∨q”都是假命题，则p真q假 C．命题“∃x∈R，x2﹣x＞0”的否定是“∀x∈R，x2﹣x＜0”‎ D．命题“能被2整除的数是偶数”的逆否命题是“不能被2整除的数不是偶数”‎ ‎8．某大学对1000名学生的自主招生水平测试成绩进行统计，得到样本频率分布直方图（如图），则这1000名学生在该次自主招生水平测试中成绩不低于70分的学生数是（　　）‎ A．300 B．400 C．500 D．600‎ ‎9．若[x]表示不超过x的最大整数，执行如图所示的程序框图，则输出的S值为（　　）‎ A．4 B．5 C．7 D．9‎ ‎10．函数f（x）=ax﹣1+3（a＞0，且a≠1）的图象过一个定点P，且点P在直线mx+ny﹣1=0（m＞0，n＞0）上，则+的最小值是（　　）‎ A．12 B．13 C．24 D．25‎ ‎11．已知P是抛物线y2=4x上一动点，则点P到直线l：2x﹣y+3=0和y轴的距离之和的最小值是（　　）‎ A． B． C．2 D．﹣1‎ ‎12．已知函数，若x1＜x2＜x3，且f（x1）=f（x2）=f（x3），则x1x2x3的取值范围是（　　）‎ A．（1，10） B．（10，12） C．N1 D．（20，24）‎ ‎　‎ 二．填空题：本大题共4小题，每小题5分 ‎13．若sin（﹣α）=，则cos（+2α）的值为　　．‎ ‎14．已知实数1，m，9构成一个等比数列，则圆锥曲线+y2=1的离心率为　　．‎ ‎15．一个多面体的三视图如图所示，则该多面体的体积是　　．‎ ‎16．某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为　　元．‎ ‎　‎ 三．解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17．已知函数f（x）=sin（2x﹣）+2cos2x﹣1．‎ ‎（Ⅰ）求函数f（x）的单调增区间；‎ ‎（Ⅱ）在△ABC中，a、b、c分别是角A、B、C的对边，且a=1，b+c=2，f（A）=，求△ABC的面积．‎ ‎18．如图，在四棱锥P﹣ABCD中，侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，AD∥BC，PA=AB=BC=2AD，E是PC的中点．‎ ‎（Ⅰ）求证：DE∥平面PAB；‎ ‎（Ⅱ）求证：平面PCD⊥平面PBC．‎ ‎19．某家电专卖店试销A，B，C三种新型空调，销售情况记录如下：‎ 第一周 第二周 第三周 第四周 第五周 A型数量（台）‎ ‎10‎ ‎10‎ ‎15‎ A4‎ A5‎ B型数量（台）‎ ‎10‎ ‎12‎ ‎13‎ B4‎ B5‎ C型数量（台）‎ ‎15‎ ‎8‎ ‎12‎ C4‎ C5‎ ‎（1）求A型空调前三周的平均周销售量；‎ ‎（2）为跟踪调查空调的使用情况，根据销售记录，从该家电专卖店前三周售出的所有空调中随机抽取一台，求抽到的空调“是B型空调或是第一周售出空调”的概率；‎ ‎（3）根据C型空调连续3周销售情况，预估C型空调连续5周的平均周销量为10台．当C型空调周销售量的方差最小时，求C4，C5的值．‎ 参考公式：‎ 样本数据x1，x2，…，xn的方差是：，其中为样本平均数．‎ ‎20．已知数列{an}的前n项和Sn=n2﹣2n．‎ ‎（1）求数列{an的通项公式an；‎ ‎（2）令bn=，求数列{bn}的前n项和Tn．‎ ‎21．垂直于x轴的直线l与椭圆C：相交于M、N两点，A是C的左顶点．‎ ‎（1）求的最小值；‎ ‎（2）设点P是C上异于M、N的任意一点，且直线MP、NP分别与x轴交于R、S两点，O是坐标原点，求△OPR和△OPS的面积之积的最大值．‎ ‎22．已知函数f（x）=lnx，．‎ ‎（1）若f（x）与g（x）在x=1处相切，试求g（x）的表达式；‎ ‎（2）若在[1，+∞）上是减函数，求实数m的取值范围；‎ ‎（3）证明不等式： ．‎ ‎　‎ ‎2016-2017学年辽宁省大连市瓦房店高中高二（上）期中数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一．选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．设全集U={1，2，3，4，5}，集合A={1，2}，B={2，3，5}，则（∁UA）∪B=（　　）‎ A．{3，5} B．{3，4，5} C．{2，3，4，5} D．{1，2，3，4}‎ ‎【考点】交、并、补集的混合运算．‎ ‎【分析】根据全集U及A，求出A的补集，找出A补集与B的并集即可．‎ ‎【解答】解：∵全集U={1，2，3，4，5}，集合A={1，2}，B={2，3，5}，‎ ‎∴∁UA={3，4，5}，‎ 则（∁UA）∪B={2，3，4，5}．‎ 故选C ‎　‎ ‎2．已知向量=（﹣3，4），=（1，m），若⊥（﹣），m=（　　）‎ A． B．7 C．﹣7 D．﹣‎ ‎【考点】平面向量数量积的运算．‎ ‎【分析】令•（﹣）=0列方程解出m．‎ ‎【解答】解：∵若⊥（﹣），∴若•（﹣）=0，即=．‎ ‎∴25=﹣3+4m，‎ 解得m=7．‎ 故选：B．‎ ‎　‎ ‎3．某高级中学有高一、二、三三个年级的学生共1600名，其中高三学生400名，如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本，则应从高三年级学生中抽取的人数是（　　）‎ A．40 B．30 C．20 D．10‎ ‎【考点】分层抽样方法．‎ ‎【分析】设应当从高三年级的学生中抽取的人数是x，则由分层抽样的定义可得，由此求出x的值．‎ ‎【解答】解：设应当从高三年级的学生中抽取的人数是x，则由分层抽样的定义可得，解得x=20，‎ 故选：C．‎ ‎　‎ ‎4．北宋 ‎ 欧阳修在《卖油翁》中写道：“（翁）乃取一葫芦置于地，以钱覆其扣，徐以杓酌油沥之，自钱孔入，而钱不湿．因曰：‘我亦无他，唯手熟尔．’”可见技能都能透过反复苦练而达至熟能生巧之境的．若铜钱是半径为1cm的圆，中间有边长为0.5cm的正方形孔，你随机向铜钱上滴一滴油，则油（油滴的大小忽略不计）正好落入孔中的概率为（　　）‎ A． B． C． D．‎ ‎【考点】几何概型．‎ ‎【分析】分别计算圆和正方形的面积，由几何概型概率公式可得．‎ ‎【解答】解：由题意可得半径为1cm的圆的面积为π×12=π，‎ 而边长为0.5cm的正方形面积为0.5×0.5=0.25，‎ 故所求概率P==，‎ 故选：B．‎ ‎　‎ ‎5．直线x﹣y+3=0被圆（x+2）2+（y﹣2）2=2截得的弦长等于（　　）‎ A． B． C．2 D．‎ ‎【考点】直线和圆的方程的应用．‎ ‎【分析】先根据点到直线的距离公式求出圆心到弦的距离即弦心距OD，然后根据垂径定理得到垂足为弦长的中点D，根据勾股定理求出弦长的一半BD，乘以2即可求出弦长AB．‎ ‎【解答】解：连接OB，过O作OD⊥AB，根据垂径定理得：D为AB的中点，‎ 根据（x+2）2+（y﹣2）2=2得到圆心坐标为（﹣2，2），半径为．‎ 圆心O到直线AB的距离OD==，而半径OB=，‎ 则在直角三角形OBD中根据勾股定理得BD==，所以AB=2BD=‎ 故选D．‎ ‎　‎ ‎6．某公司为确定明年投入某产品的广告支出，对近5年的广告支出m与销售额y（单位：百万元）进行了初步统计，得到下列表格中的数据：‎ y ‎30‎ ‎40‎ p ‎50‎ ‎70‎ m ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ 经测算，年广告支出m与年销售额y满足线性回归方程=6.5m+17.5，则p的值为（　　）‎ A．45 B．50 C．55 D．60‎ ‎【考点】线性回归方程．‎ ‎【分析】求出，代入回归方程计算，从而得出p的值．‎ ‎【解答】解： ==5，‎ ‎∴=6.5×5+17.5=50，‎ ‎∴=50，解得p=60．‎ 故选：D．‎ ‎　‎ ‎7．下列结论正确的是（　　）‎ A．“x≠1”是“x2≠1”的充分不必要条件 B．若“p∧q”与“¬p∨q”都是假命题，则p真q假 C．命题“∃x∈R，x2﹣x＞0”的否定是“∀x∈R，x2﹣x＜0”‎ D．命题“能被2整除的数是偶数”的逆否命题是“不能被2整除的数不是偶数”‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】A，x=﹣1时，x2=1； B，¬p∨q是假命题时，则p真q假，则 p∧q 是假命题； C，命题“∃x∈R，x2﹣x＞0”的否定是“∀x∈R，x2﹣x≤0；‎ D，命题“能被2整除的数是偶数”的逆否命题是“若一个数不是偶数 则不能被2整除；‎ ‎【解答】解：对于A，x=﹣1时，x2=1也成立，故错； ‎ 对于 B，¬p∨q是假命题时，则p真q假，则 p∧q 是一定是假命题，故正确； ‎ 对于C，命题“∃x∈R，x2﹣x＞0”的否定是“∀x∈R，x2﹣x≤0，故错；‎ D，命题“能被2整除的数是偶数”的逆否命题是“若一个数不是偶数 则不能被2整除，故错； ‎ 故选：B．‎ ‎　‎ ‎8．某大学对1000名学生的自主招生水平测试成绩进行统计，得到样本频率分布直方图（如图），则这1000名学生在该次自主招生水平测试中成绩不低于70分的学生数是（　　）‎ A．300 B．400 C．500 D．600‎ ‎【考点】频率分布直方图．‎ ‎【分析】根据频率分布直方图，算出成绩不低于70分的3个组的面积之和为0.6，从而得到成绩不低于70分的学生的频率为0.6，由此即可得到这1000名学生在该次自主招生水平测试中不低于70分的学生数．‎ ‎【解答】解：根据频率分布直方图，可得 成绩在70﹣80的小组的小矩形面积为S1=10×0.035=0.35；在80﹣90的小组的小矩形面积为S2=10×0.015=0.15‎ 在90﹣100的小组的小矩形面积为S3=10×0.010=0.10‎ ‎∴成绩不低于70分的学生所在组的面积之和为S=S1+S2+S3=0.6‎ 即成绩不低于70分的学生的频率为0.6，由此可得 这1000名学生在该次自主招生水平测试中不低于70分的学生数是1000×0.6=600‎ 故选：D．‎ ‎　‎ ‎9．若[x]表示不超过x的最大整数，执行如图所示的程序框图，则输出的S值为（　　）‎ A．4 B．5 C．7 D．9‎ ‎【考点】程序框图．‎ ‎【分析】根据题意，模拟程序框图的运行过程，求出该程序运行后输出的S的值．‎ ‎【解答】解：模拟程序框图的运行过程，如下；‎ S=0，n=0，S=0+[]=0，0＞4，否；‎ n=1，S=0+[]=1，1＞4，否；‎ n=2，S=1+[]=2，2＞4，否；‎ n=3，S=2+[]=3，3＞4，否；‎ n=4，S=3+[]=5，4＞4，否；‎ n=5，S=5+[]=7，5＞4，是；‎ 输出S=7．‎ 故选：C．‎ ‎　‎ ‎10．函数f（x）=ax﹣1+3（a＞0，且a≠1）的图象过一个定点P，且点P在直线mx+ny﹣1=0（m＞0，n＞0）上，则+的最小值是（　　）‎ A．12 B．13 C．24 D．25‎ ‎【考点】基本不等式．‎ ‎【分析】函数f（x）=ax﹣1+3（a＞0，且a≠1）的图象过一个定点P（1，4），可得m+4n=1．再利用“乘1法”与基本不等式的性质即可得出．‎ ‎【解答】解：函数f（x）=ax﹣1+3（a＞0，且a≠1）的图象过一个定点P（1，4），‎ ‎∵点P在直线mx+ny﹣1=0（m＞0，n＞0）上，‎ ‎∴m+4n=1．‎ 则+=（m+4n）=17+≥17+4×2=25，当且仅当m=n=时取等号．‎ 故选：D．‎ ‎　‎ ‎11．已知P是抛物线y2=4x上一动点，则点P到直线l：2x﹣y+3=0和y轴的距离之和的最小值是（　　）‎ A． B． C．2 D．﹣1‎ ‎【考点】抛物线的简单性质．‎ ‎【分析】作图，化点P到直线l：2x﹣y+3=0和y轴的距离之和为PF+PA﹣1，从而求最小值．‎ ‎【解答】解：由题意作图如右图，‎ 点P到直线l：2x﹣y+3=0为PA；‎ 点P到y轴的距离为PB﹣1；‎ 而由抛物线的定义知，‎ PB=PF；‎ 故点P到直线l：2x﹣y+3=0和y轴的距离之和为PF+PA﹣1；‎ 而点F（1，0）到直线l：2x﹣y+3=0的距离为 ‎=；‎ 故点P到直线l：2x﹣y+3=0和y轴的距离之和的最小值为﹣1；‎ 故选D．‎ ‎　‎ ‎12．已知函数，若x1＜x2＜x3，且f（x1）=f（x2）=f（x3），则x1x2x3的取值范围是（　　）‎ A．（1，10） B．（10，12） C．N1 D．（20，24）‎ ‎【考点】函数的值．‎ ‎【分析】作函数的图象，从而结合图象可知lgx1=lgx2=﹣x3+6，从而求得．‎ ‎【解答】解：作函数的图象如下，‎ ‎，‎ ‎∵x1＜x2＜x3，f（x1）=f（x2）=f（x3），‎ ‎∴﹣lgx1=lgx2=﹣x3+6，‎ ‎∴x1x2=1，10＜x3＜12，‎ ‎∴10＜x1x2x3＜12．‎ 故选：B．‎ ‎　‎ 二．填空题：本大题共4小题，每小题5分 ‎13．若sin（﹣α）=，则cos（+2α）的值为　　．‎ ‎【考点】二倍角的余弦；角的变换、收缩变换．‎ ‎【分析】利用二倍角的余弦公式把要求的式子化为2﹣1，再利用诱导公式化为2﹣1，将条件代入运算求得结果．‎ ‎【解答】解：∵=cos2（+α）=2﹣1=2﹣1 ‎ ‎=2×﹣1=，‎ 故答案为：．‎ ‎　‎ ‎14．已知实数1，m，9构成一个等比数列，则圆锥曲线+y2=1的离心率为　或2　．‎ ‎【考点】椭圆的简单性质；双曲线的简单性质．‎ ‎【分析】由1，m，9构成一个等比数列，得到m=±3．当m=3时，圆锥曲线是椭圆；当m=﹣3时，圆锥曲线是双曲线，由此入手能求出离心率．‎ ‎【解答】解：∵1，m，9构成一个等比数列，‎ ‎∴m=±3．‎ 当m=3时，圆锥曲线+y2=1是椭圆，它的离心率是=；‎ 当m=﹣3时，圆锥曲线+y2=1是双曲线，它的离心率是2．‎ 故答案为：或2．‎ ‎　‎ ‎15．一个多面体的三视图如图所示，则该多面体的体积是　　．‎ ‎【考点】由三视图求面积、体积．‎ ‎【分析】判断几何体的形状，结合三视图的数据，求出几何体的体积．‎ ‎【解答】解：由三视图可知，该多面体是由正方体截去两个正三棱锥所成的几何体，如图，‎ 正方体棱长为2，正三棱锥侧棱互相垂直，侧棱长为1，‎ V=V正方体﹣2V三棱锥=2×2×2=．‎ 故答案我：‎ ‎　‎ ‎16．某高科技企业生产产品A和产品B需要甲、乙两种新型材料．生产一件产品A需要甲材料1.5kg，乙材料1kg，用5个工时；生产一件产品B需要甲材料0.5kg，乙材料0.3kg，用3个工时，生产一件产品A的利润为2100元，生产一件产品B的利润为900元．该企业现有甲材料150kg，乙材料90kg，则在不超过600个工时的条件下，生产产品A、产品B的利润之和的最大值为　216000　元．‎ ‎【考点】简单线性规划的应用．‎ ‎【分析】设A、B两种产品分别是x件和y件，根据题干的等量关系建立不等式组以及目标函数，利用线性规划作出可行域，通过目标函数的几何意义，求出其最大值即可；‎ ‎【解答】解：（1）设A、B两种产品分别是x件和y件，获利为z元．‎ 由题意，得，z=2100x+900y．‎ 不等式组表示的可行域如图：由题意可得，解得：，A（60，100），‎ 目标函数z=2100x+900y．经过A时，直线的截距最大，目标函数取得最大值：2100×60+900×100=216000元．‎ 故答案为：216000．‎ ‎　‎ 三．解答题：解答应写出文字说明，证明过程或演算步骤.‎ ‎17．已知函数f（x）=sin（2x﹣）+2cos2x﹣1．‎ ‎（Ⅰ）求函数f（x）的单调增区间；‎ ‎（Ⅱ）在△ABC中，a、b、c分别是角A、B、C的对边，且a=1，b+c=2，f（A）=，求△ABC的面积．‎ ‎【考点】正弦函数的单调性；余弦定理．‎ ‎【分析】（Ⅰ）函数f（x）展开后，利用两角和的公式化简为一个角的一个三角函数的形式，结合正弦函数的单调增区间求函数f（x）的单调增区间．‎ ‎（Ⅱ）利用f（A）=，求出A的大小，利用余弦定理求出bc的值，然后求出△ABC的面积．‎ ‎【解答】解：（Ⅰ）因为=‎ ‎=‎ ‎=‎ 所以函数f（x）的单调递增区间是〔〕（k∈Z）‎ ‎（Ⅱ）因为f（A）=，所以 又0＜A＜π所以 从而故A=‎ 在△ABC中，∵a=1，b+c=2，A=‎ ‎∴1=b2+c2﹣2bccosA，即1=4﹣3bc．‎ 故bc=1‎ 从而S△ABC=‎ ‎　‎ ‎18．如图，在四棱锥P﹣ABCD中，侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，AD∥BC，PA=AB=BC=2AD，E是PC的中点．‎ ‎（Ⅰ）求证：DE∥平面PAB；‎ ‎（Ⅱ）求证：平面PCD⊥平面PBC．‎ ‎【考点】平面与平面垂直的判定；直线与平面平行的判定．‎ ‎【分析】（Ⅰ）取PB中点F，连接EF，AF，推导出四边形DEFA是平行四边形，由此能证明DE∥平面PAB． ‎ ‎（Ⅱ）由已知推导出AF⊥BC，AF⊥PB，从而AF⊥平面PBC，再由DE∥AF，能证明平面PCD⊥平面PBC．‎ ‎【解答】证明：（Ⅰ）取PB中点F，连接EF，AF，‎ 由已知EF∥BC∥AD，且2EF=2AD=BC，‎ 所以，四边形DEFA是平行四边形，‎ 于是DE∥AF，AF⊂平面PAB，DE⊄平面PAB，‎ 因此DE∥平面PAB． …‎ ‎（Ⅱ）侧面PAB⊥底面ABCD，且∠PAB=∠ABC=90°，‎ 所以BC⊥平面PAB，AF⊂平面PAB，所以AF⊥BC，‎ 又因为PA=AB，F是PB中点，于是AF⊥PB，‎ PB∩BC=B，所以AF⊥平面PBC，‎ 由（Ⅰ）知DE∥AF，故DE⊥平面PBC，‎ 而DE⊂平面PCD，‎ 因此平面PCD⊥平面PBC． …‎ ‎　‎ ‎19．某家电专卖店试销A，B，C三种新型空调，销售情况记录如下：‎ 第一周 第二周 第三周 第四周 第五周 A型数量（台）‎ ‎10‎ ‎10‎ ‎15‎ A4‎ A5‎ B型数量（台）‎ ‎10‎ ‎12‎ ‎13‎ B4‎ B5‎ C型数量（台）‎ ‎15‎ ‎8‎ ‎12‎ C4‎ C5‎ ‎（1）求A型空调前三周的平均周销售量；‎ ‎（2）为跟踪调查空调的使用情况，根据销售记录，从该家电专卖店前三周售出的所有空调中随机抽取一台，求抽到的空调“是B型空调或是第一周售出空调”的概率；‎ ‎（3）根据C型空调连续3周销售情况，预估C型空调连续5周的平均周销量为10台．当C型空调周销售量的方差最小时，求C4，C5的值．‎ 参考公式：‎ 样本数据x1，x2，…，xn的方差是：，其中为样本平均数．‎ ‎【考点】极差、方差与标准差．‎ ‎【分析】（1）根据数表中的数值计算平均数即可；‎ ‎（2）方法1：根据概率的定义进行计算即可；‎ 方法2：利用对立事件的概率公式进行计算也可；‎ ‎（3）根据方差的定义可得S2的解析式，再根据二次函数性质求出 c4=7或c4=8时，S2取得最小值，从而求出c5的值．‎ ‎【解答】解：（1）A型空调前三周的平均销售量为 ‎（台）；…‎ ‎（2）方法1：从前三周售出的所有空调中随机抽取一台，有105种可能，‎ 其中“是B型或是第一周售出空调”有35+35﹣10=60；…‎ 因此抽到的空调“是B型或是第一周售出空调”的概率是；…‎ 方法2：设抽到的空调“不是B型也不是第一周售出空调”的事件是M，‎ 抽到的空调“是B型或是第一周售出空调”的事件是N，‎ 则，‎ ‎；…‎ 故抽到的空调“是B型或是第一周售出空调”的概率是；…‎ ‎（3）因为C型空调平均周销售量为10台，‎ 所以c4+c5=10×5﹣15﹣8﹣12=15；…‎ 又，‎ 化简得．…‎ 因为c4∈N，‎ 所以c4=7或c4=8时，S2取得最小值，‎ 此时C5=8或C5=7…‎ ‎　‎ ‎20．已知数列{an}的前n项和Sn=n2﹣2n．‎ ‎（1）求数列{an的通项公式an；‎ ‎（2）令bn=，求数列{bn}的前n项和Tn．‎ ‎【考点】数列的求和．‎ ‎【分析】（1）由题意得，当n=1时a1=s1=﹣1，当n≥2时an=sn﹣sn﹣1=2n﹣3，再验证n=1时是否成立即可；‎ ‎（2）由（1）和题意求出bn，利用错位相减法求出数列{bn}的前n项和Tn．‎ ‎【解答】解：（1）当n=1时，a1=s1=1﹣2=﹣1…‎ 当n≥2时，an=sn﹣sn﹣1=n2﹣2n﹣[（n﹣1）2﹣2（n﹣1）]=2n﹣3…‎ 又a1=﹣1=2﹣3，也符合上式，…‎ 因此，an=2n﹣3…‎ ‎（2）由（1）得，bn==，‎ 所以Tn= ①，‎ Tn= ②，‎ ‎①﹣②得， Tn=+2（）﹣‎ ‎=+2×﹣=‎ 所以Tn=．‎ ‎　‎ ‎21．垂直于x轴的直线l与椭圆C：相交于M、N两点，A是C的左顶点．‎ ‎（1）求的最小值；‎ ‎（2）设点P是C上异于M、N的任意一点，且直线MP、NP分别与x轴交于R、S两点，O是坐标原点，求△OPR和△OPS的面积之积的最大值．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】（1）点M、N关于x轴对称，设M（x1，y1）（y1＞0），则N（x1，﹣y1），利用数量积运算性质、二次函数的单调性即可得出．‎ ‎（2）利用点与椭圆的位置关系、三角形面积计算公式即可得出．‎ ‎【解答】解：（1）点M、N关于x轴对称，设M（x1，y1）（y1＞0），则N（x1，﹣y1），‎ ‎∵A（﹣2，0），∴，，‎ ‎∵点M在C上，∴，‎ ‎∴，‎ ‎∵x1∈（﹣2，2），∴时，取最小值．‎ ‎（2）设P（x0，y0），则直线MP的方程为：，‎ 令y=0，得，同理，‎ ‎∵点M、P在C上，∴，，‎ ‎∴，‎ ‎，‎ ‎∵y0∈[﹣1，1]，∴y0=±1时，S△OPS•S△OPR取最大值1．‎ ‎　‎ ‎22．已知函数f（x）=lnx，．‎ ‎（1）若f（x）与g（x）在x=1处相切，试求g（x）的表达式；‎ ‎（2）若在[1，+∞）上是减函数，求实数m的取值范围；‎ ‎（3）证明不等式： ．‎ ‎【考点】利用导数研究函数的单调性；利用导数研究曲线上某点切线方程．‎ ‎【分析】（1）求导数，利用f（x）与g（x）在x=1处相切，可求g（x）的表达式；‎ ‎（2）在[1，+∞）上是减函数，可得导函数小于等于0，在[1，+∞）上恒成立，分离参数，利用基本不等式，可求实数m的取值范围；‎ ‎（3）当x≥2时，证明，当x=2时，当x=3时，当x=4时，…，当x=n+1时，利用叠加法，即可得到结论．‎ ‎【解答】解：（1）∵f（x）=lnx，∴，∴，得：a=2．‎ 又∵，∴b=﹣1，‎ ‎∴g（x）=x﹣1；‎ ‎（2）=在[1，+∞）上是减函数，‎ ‎∴在[1，+∞）上恒成立．‎ 即x2﹣（2m﹣2）x+1≥0在[1，+∞）上恒成立，由，x∈[1，+∞），‎ ‎∵，‎ ‎∴2m﹣2≤2得m≤2；‎ 证明：（3）由（1）可得：当x≥2时：，∴得：，‎ ‎∴．‎ 当x=2时：，‎ 当x=3时：，‎ 当x=4时：，‎ ‎…‎ 当x=n+1时：，n∈N+，n≥2，‎ 上述不等式相加得： ，‎ 即： ．‎ ‎　‎