数学理卷·2018届黑龙江省实验中学高三上学期12月月考（2017 8页

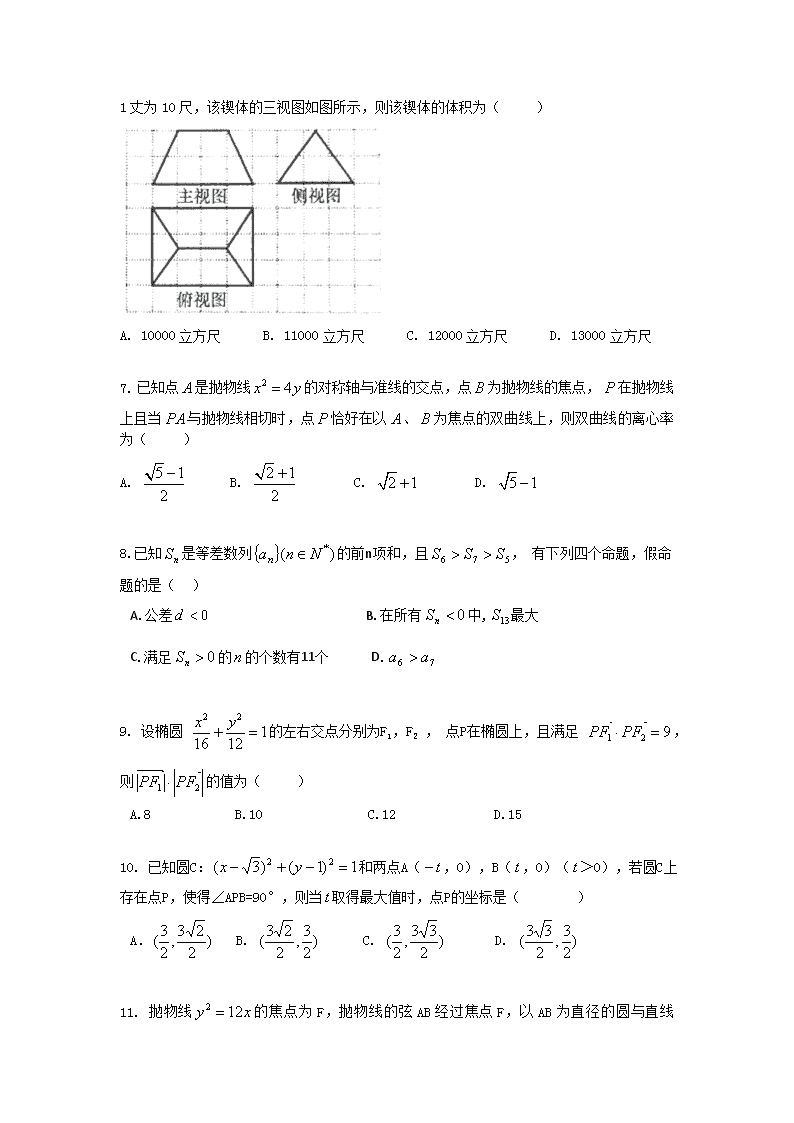
黑龙江省实验中学高三学年12月月考 数学理科 考试时间120分钟 总分150分 命题人：王晓红 审题人：李庆亮 一、选择题（每题5分，共60分）‎ ‎1．已知集合，集合，则等于（ ）‎ A. B. C. D. ‎ ‎2．给出下列三个命题：‎ 或是“”的必要不充分条件 若，则 那么，下列命题为真命题的是（ ）‎ A. B. C. D. ‎ ‎3．若i为虚数单位，设复数z满足| z |=1，则|z-1+i|的最小值为（ ）‎ A. -1 B. 2- C. +1 D. 2+‎ ‎4．已知为两条不同的直线， 为两个不同的平面，且， ，则下列命题中的假命题是（ ）‎ A. 若∥，则∥ B. 若，则 C. 若相交，则相交 D. 若相交，则相交 ‎5．设变量，满足，若直线经过该可行域，则的最大值为（ ）‎ A． B． C． D．‎ ‎ ‎ ‎6．‎ ‎《九章算术》是我国古代内容极为丰富的数学名著，书中有如下问题：“今有刍甍，下广三丈，袤四丈，上袤二丈，无广，高二丈，问积几何？”其意思为：“今有底面为矩形的屋脊状的锲体，下底面宽3丈，长4丈，上棱长2丈，高2丈，问：它的体积是多少？”已知1丈为10尺，该锲体的三视图如图所示，则该锲体的体积为（ ）‎ A. 10000立方尺 B. 11000立方尺 C. 12000立方尺 D. 13000立方尺 ‎7. 已知点是抛物线的对称轴与准线的交点，点为抛物线的焦点， 在抛物线上且当与抛物线相切时，点恰好在以、为焦点的双曲线上，则双曲线的离心率为（ ）‎ A. B. C. D. ‎ ‎8.已知是等差数列的前n项和，且， 有下列四个命题，假命题的是（     ） ‎ A.公差 B.在所有中,最大 C.满足的的个数有11个 D.‎ ‎9. 设椭圆 的左右交点分别为F1，F2 ， 点P在椭圆上，且满足 ，则的值为（   ） ‎ A.8 B.10 C.12 D.15‎ ‎10. 已知圆C：和两点A（，0），B（，0）（＞0），若圆C上存在点P，使得∠APB=90°，则当取得最大值时，点P的坐标是（   ） ‎ A． B. C. D. ‎ ‎11. 抛物线的焦点为F，抛物线的弦AB经过焦点F，以AB为直径的圆与直线 相切于，则线段AB的长为（ ）‎ A. 24 B. 18 C. 16 D. 12 ‎ ‎12. 当 时， 恒成立，则的取值范围为（ ）‎ A. B. C. D. ‎ 二、填空题（每题5分共20分）‎ ‎13. 已知，若，则的最小值为__________．‎ ‎14．已知焦距为的双曲线的左右顶点分别为是双曲线上异于的任意两点，若 依次成等比数列，则双曲线的标准方程是__________.‎ ‎15．若， ，则__________.‎ ‎16．在中， , .若为的外心，则______．‎ 三、解答题(共计70分)‎ ‎17．（本题满分10分）(1)设，且，求证：. ‎ ‎(2)设 为不全相等的正数，且，求证：.‎ ‎18.（本题满分12分）如图，四棱锥中，⊥平面,是矩形，，‎ 直线与底面所成的角等于30°,， .‎ ‎(1)若∥平面，求的值；‎ ‎(2)当等于何值时，二面角的大小为45°？‎ A P D C B E F ‎19.（本题满分12分）在中， 是边的中点，记 ‎（1）求的大小；‎ ‎（2）当取最大值时，求的值.‎ ‎20. （本题满分12分）设为数列的前项和， ，且，记为数列的前项和，（1）求证：数列{ }是等比数列，并求得通项公式；（2）求。‎ ‎21. （本题满分12分）设是椭圆的左焦点，直线为，直线与轴交于点，、为椭圆的左右顶点．已知，且．‎ ‎（Ⅰ）若过点的直线与椭圆相交于不同的两点，求证：；‎ ‎（Ⅱ）求的面积的最大值． ‎ ‎22. （本题满分12分）已知函数 （1） 若曲线在处的切线与直线垂直，求的值；并判断此时的单调性；‎ （2） 若有两个极值点，且，当恒成立时，求m的取值范围。‎ 数学：‎ ‎1． D 2． C 3． A 4．D 5． A 6．A 7. C 8.C 9. D 10．D 11.A 12． A ‎13．96 14． 15． 16．288‎ ‎17．(1) 方法一(分析法)：要证 a3+b3>a2b+ab2 成立，即需证(a+b)(a2-ab+b2) >ab(a+b) 成立.又因 a+b>0 ，故只需证a2-ab+b2>ab 成立，即需证 a2-ab+b2>0 成立，即需证 (a-b)2>0 成立.而依题设 ，则 (a-b)2>0 显然成立.由此命题得证.‎ 方法二(综合法)：.‎ 注意到 ， a+b>0 ，由上式即得 ‎(a+b)(a2-ab+b2) >ab(a+b) . 所以 a3+b3>a2b+ab2 . ‎ ‎（2）解：∵a ， b ， c为不全相等的正数，且 abc=1 ，‎ ‎∴ .‎ 又  ，‎ ‎，  ，且a ， b ， c不全相等，∴上述三个不等式中的“=”不能同时成立.‎ ‎∴  ，即  .‎ 故 . ‎ ‎18． 解：（1）∵平面PBC平面PAC=AC，EF平面PBC，若EF∥平面PAC，‎ 则EF∥PC，又F是PB的中点，∴E为BC的中点，∴‎ ‎(2)以A为坐标原点，分别以AD、AB、AP所在直线为轴、轴、轴 建立空间直角坐标系，则P（0，0，1），B（0，1，0），F（0，，），‎ D（，0，0）, 设，则E（，1，0）‎ 求得平面PDE的法向量（，平面ADE的法向量，‎ ‎∴，‎ 解得或（舍去）,所以当时，二面角的大小45°。‎ ‎19．（1）因为，所以，即，整理得，又，所以，即 ‎（2），令，‎ 因为,所以，在中， ，‎ 所以，当且仅当时取等号，此时， 为正，所以当取最大值时， ‎ ‎20．（1）由2an﹣an﹣1=3•2n﹣1（n≥2），得 ∴ ，‎ 由2an﹣an﹣1=3•2n﹣1（n≥2），且3a1=2a2， 可得2a2﹣a1=6，即2a1=6，得a1=3．‎ ‎∴数列{ }是以为首项，以为公比的等比数列，‎ 则 ‎ ‎（2）∴+（2+22+23+…+2n）= =2•2n﹣21﹣n ‎ ，根据等比数列求和公式： ‎ 故答案为： 。‎ ‎21．解：（Ⅰ）因为，所以．又因为，所以，即，‎ 所以或（舍去），所以，，‎ 所以椭圆方程为．‎ 当直线的斜率为时，显然，满足题意．‎ 当直线的斜率不为时，设，此时设直线的方程为，代入椭圆方程，整理得则，即． 由韦达定理知，‎ 所以，从而．‎ ‎（Ⅱ） ‎ ‎，当且仅当，即（此时满足的条件）时取得等号，故的面积的最大值是． ‎ ‎22.（1）解：，所以在为增函数。 ‎ （2） 令 所以，为减函数，所以 ‎