- 361.50 KB
- 2021-07-01 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
2018-2019学年湖南省长沙市长郡中学高一上学期期中考试数学试题
时量:120分钟 满分:100分
一、选择题(本大题共15小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图中阴影部分用集合可表示为
2.下列四组函数,表示同一函数的是
3.已知00时,,则f(-1)=
A.-2 B.0 C.1 D.2
6.奇函数f(x)在区间[3,6]上是增函数,在区间[3,6]上的最大值为8,最小值为-2,则的值为
A.10 B.-10 C.9 D.15
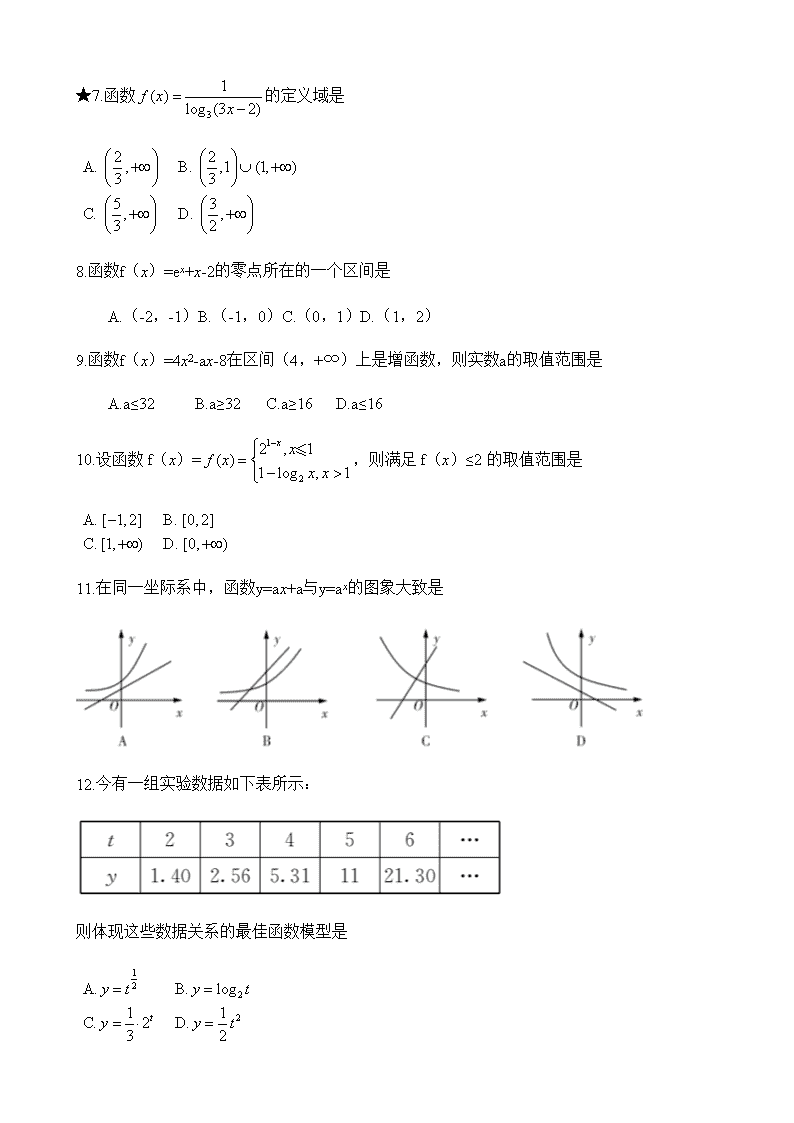
★7.函数的定义域是
8.函数f(x)=ex+x-2的零点所在的一个区间是
A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)
9.函数f(x)=4x2-ax-8在区间(4,+∞)上是增函数,则实数a的取值范围是
A.a≤32 B.a≥32 C.a≥16 D.a≤16
10.设函数f(x)=,则满足f(x)≤2的取值范围是
11.在同一坐际系中,函数y=ax+a与y=ax的图象大致是
12.今有一组实验数据如下表所示:
则体现这些数据关系的最佳函数模型是
13.在直角梯形ABCD中,AB⊥BC,AD=DC=2,CB=,动点P从点A出发,由A→D→C→B沿边运动(如图所示),P在AB上的射影为Q,设点P运动的路程为x,△APQ的面积为y,则y=f(x)的图象大致是
14.已知偶函数f(x)在(-∞,0)上单调递减,且f(2)=0,则关于x的不等式xf(x)<0的解集是
A.(-2,2)
B.(-2,0)∪(0,2)
C.(-2,0)∪(2,+∞)
D.(-∞,-2)∪(0,2)
15.用C(A)表示非空集合A中元素的个数,定义A*B=,若A={1,2},B={x(x2+ax)(x2+ax+2)=0},且A*B=1,设实数a的所有可能取值构成集合S,则C(S)=
A.4B.3C.2D.1
二、填空题(本大题共5小题,每小题3分,共15分.)
16.计算:2-1+lg 100-ln=_____.
★17.已知幂函数f(x)的图象经过点(2,),且f(x0)=3,则x0=____.
18.设f(x)=ax2+bx+2是定义在[1+a,2]上的偶函数,则f(x)的值域是____.
19.已知函数y=6+c2+2x(a,b是常数,且a>0.a≠1)在区间[-,0]上有ymax=3,ymax=号,则常数a的值等于_____.
20.已知m∈R,函数,若函数y=f(g(x))- m有6个零点,则实数m的取值范围是_____。三、解答题(本大题共5小题,每小题8分,共40分.解答应写出文字说明,证明过程或演算步骤.)
21.(本小题满分8分)已知集合.
(1)若a=1,求M∩N;
(2)若,求实数a的取值范围.
★22.(本小题满分8分)
对于函数.
(1)判断并证明函数的单调性;
(2)是否存在实数a,使函数f(x)为奇函数?证明你的结论.
23.(本小题满分8分)
一次函数f(x)是R上的增函数,g(x)=f(x)(x+m),已知f[f(x)]=16x+5.
(1)求f(x);
(2)当x∈[-1,3]时,g(x)有最大值13,求实数m的值.
24.(本小题满分8分)
某公司为提高员工的综合素质,聘请专业机构对员工进行专业技术培训,其中培训机构费用成本为12000元.公司每位员工的培训费用按以下方式与该机构结算:若公司参加培训的员工人数不超过30人时,每人的培训费用为850元;若公司参加培训的员工人数多于30人,则给予优惠:每多一人,培训费减少10元.已知该公司最多有60位员工可参加培训,设参加培训的员工人数为x人,每位员工的培训费为y元,培训机构的利润为Q元.
(1)写出y与x(x>0,x∈N*)之间的函数关系式:
(2)当公司参加培训的员工为多少人时,培训机构可获得最大利润?并求最大利润,
25.(本小题满分8分)
设f(x)是R上的奇函数,且当x>0时,f(x)=lg(x2-ax+17),a∈R.
(1)若f(1)=1,求f(x)的解析式;
(2)若a=0,不等式f(k·2x)+f(4x+k+1)>0恒成立,求实数k的取值范围;
(3)若f(x)的值域为R,求a的取值范围.
数学参考答案
一、选择题(本大题共15小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1-15.ABADA ABCAD BCDDB
14.D
15.B
二、填空题(本大题共5小题,每小题3分,共15分.)
16.2
17.9
18.[-10,2]
19.2或
20.(0.)
三、解答题(本大题共5小题,每小题8分,共40分.解答应写出文字说明,证明过程或演算步骤.)
21.【解析】
(1)
(2),若,则a≥2.