2021版高考化学一轮复习热点突破微课7晶体综合计算练习含解析鲁科版 6页

晶体综合计算 ‎1.金属晶胞结构的相关计算 ‎(1)晶胞质量=晶胞占有的微粒的质量=晶胞占有的微粒数×。‎ ‎(2)晶体中体心立方堆积、面心立方堆积中的几组公式(设棱长为a)‎ ‎①面对角线长=a。‎ ‎②体对角线长=a。‎ ‎③体心立方堆积4r=a(r为原子半径)。‎ ‎④面心立方堆积4r=a(r为原子半径)。 ‎ ‎(3)空间利用率=。‎ ‎2.涉及晶胞图的相关计算步骤 ‎(1)计算晶胞中的粒子数目或计算化学式。‎ ‎(2)计算晶胞参数,如密度、摩尔质量、粒子在空间的坐标点。‎ ‎(3)计算晶胞中粒子之间的距离。‎ ‎【典例】(2019·全国卷Ⅰ)图(a)是MgCu2的拉维斯结构,Mg以金刚石方式堆积,八面体空隙和半数的四面体空隙中,填入以四面体方式排列的Cu。‎ 图(b)是沿立方格子对角面取得的截图。可见,Cu原子之间最短距离x=__________pm,Mg原子之间最短距离y=______________pm。 ‎ 设阿伏加德罗常数的值为NA,则MgCu2的密度是__________g·cm-3(列出计算表达式)。 ‎ - 6 -‎ 思维建模计算晶体密度和晶体中微粒间距离的思维模式 ‎(1)计算晶体密度的计算流程 ‎(2)晶体中微粒间距离的计算流程 ‎【解析】根据晶胞结构可知Cu原子之间最短距离为面对角线的,由于边长是 a pm,则面对角线是a pm,则x=a pm;Mg原子之间最短距离为体对角线的,由于边长是a pm,则体对角线是a pm,则y=a;根据晶胞结构可知晶胞中含有镁原子的个数是8×+6×+4=8,则Cu原子个数为16,晶胞的质量是 ‎ g。由于边长是a pm,则MgCu2的密度是 g·cm-3。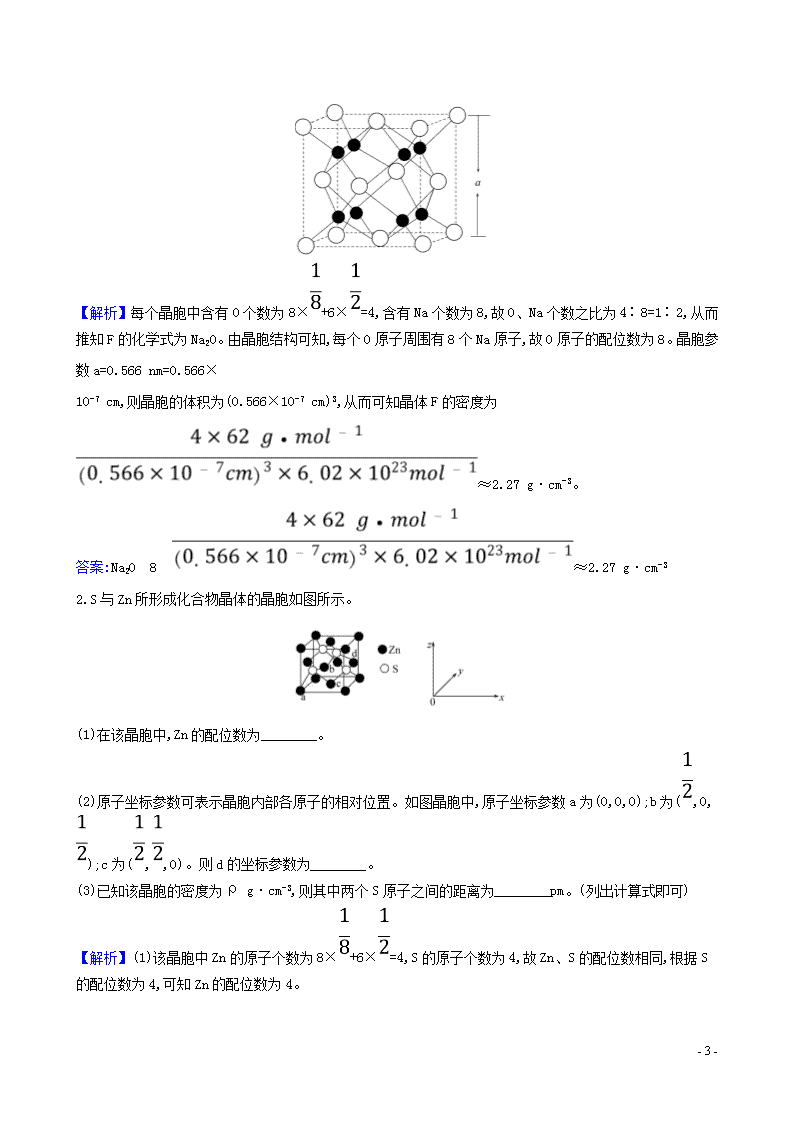‎ 答案:a　　a　　‎ ‎1.O和Na能够形成化合物F,其晶胞结构如图所示,晶胞参数a=0.566 nm,F的化学式为________;晶胞中O原子的配位数为________________;列式计算晶体F的密度(g·cm-3):____________________。 ‎ - 6 -‎ ‎【解析】每个晶胞中含有O个数为8×+6×=4,含有Na个数为8,故O、Na个数之比为4∶8=1∶2,从而推知F的化学式为Na2O。由晶胞结构可知,每个O原子周围有8个Na原子,故O原子的配位数为8。晶胞参数a=0.566 nm=0.566×‎ ‎10‎-7 cm,则晶胞的体积为(0.566×10‎-7 cm)3,从而可知晶体F的密度为≈‎2.27 g·cm-3。‎ 答案:Na2O　8　≈‎2.27 g·cm-3‎ ‎2.S与Zn所形成化合物晶体的晶胞如图所示。‎ ‎(1)在该晶胞中,Zn的配位数为________。 ‎ ‎(2)原子坐标参数可表示晶胞内部各原子的相对位置。如图晶胞中,原子坐标参数a为(0,0,0);b为(,0,);c为(,,0)。则d的坐标参数为________。 ‎ ‎(3)已知该晶胞的密度为ρ g·cm-3,则其中两个S原子之间的距离为________pm。(列出计算式即可) ‎ ‎【解析】(1)该晶胞中Zn的原子个数为8×+6×=4,S的原子个数为4,故Zn、S的配位数相同,根据S的配位数为4,可知Zn的配位数为4。‎ - 6 -‎ ‎(2)根据d的位置,可知其坐标参数为(1,,)。‎ ‎(3)根据S原子的位置可知,两个S原子之间的距离为晶胞边长的,设晶胞边长为a pm,则该晶胞的质量为 g=ρ g·cm-3×(a×10‎-10 cm)3,解得a=×1010,故两个S原子之间的距离为××1010 pm。‎ 答案:(1)4　(2)(1,,)　(3)××1010‎ ‎【加固训练】‎ ‎1.按要求回答下列问题:‎ ‎(1)立方氮化硼晶胞结构如图所示,若晶胞边长为361.5 pm,则立方氮化硼的密度是________ g·cm-3(只要求列算式,不必计算出数值,阿伏加德罗常数的值为NA)。 ‎ ‎(2)F跟Ca可形成离子化合物,其晶胞结构如图。该离子化合物晶体的密度为 ρ g·cm-3,则晶胞的体积是________(用含ρ的代数式表示)。 ‎ ‎(3)Cu与F形成的化合物的晶胞结构如图所示,若晶体密度为a g·cm-3,则Cu与F最近距离为__________ pm。 ‎ ‎(阿伏加德罗常数用NA表示,列出计算表达式,不用化简;图中为Cu,为F)‎ - 6 -‎ ‎【解析】(1)一个立方氮化硼晶胞中含有4个N原子和4个B原子。一个晶胞的质量为×‎4 g,一个立方氮化硼晶胞的体积是(361.5 pm)3,因此立方氮化硼的密度是 g·cm-3。(2)根据晶胞结构可以知道一个CaF2晶胞中有4个Ca和8个F,氟化钙的摩尔质量为‎78 g·mol-1,一个晶胞的质量为 g,则晶胞的体积为 cm3,代入NA的值可求得为 cm3。(3)设晶胞的棱长为x cm,在晶胞中,Cu:8×+6×=4;F:4,其化学式为CuF。a·x3·NA=‎4M(CuF), x=。最短距离为小立方体体对角线的,小立方体的体对角线为x。所以最短距离为·×1010 pm。‎ 答案:(1)　(2) cm3‎ ‎(3)·×1010‎ ‎2.Ni和La的合金是目前使用广泛的储氢材料,具有大容量、高寿命、耐低温等特点,在我国已实现了产业化。该合金的晶胞结构如图所示。‎ - 6 -‎ ‎(1)该晶体的化学式为________________。 ‎ ‎(2)已知该合金的摩尔质量为M g·mol-1,密度为d g·cm-3,设NA为阿伏加德罗常数的值,则该晶胞的体积是______ cm3(用含M、d、NA的代数式表示)。 ‎ ‎(3)该晶体的内部具有空隙,且每个晶胞的空隙中储存6个氢原子时比较稳定。已知:a=511 pm,c=397 pm;标准状况下氢气的密度为8.98×10‎-5 g·cm-3;储氢能力=。若忽略储氢前后晶胞的体积变化,则该储氢材料的储氢能力为____________。 ‎ ‎【解析】(1)由晶胞结构图可知,1个晶胞中La的原子个数为8×=1,Ni的原子个数为8×+1=5,则该晶体的化学式为LaNi5。(2)1个晶胞的质量m=,由V=可知1个晶胞的体积V= cm3。‎ ‎(3)LaNi5合金储氢后氢气的密度ρ==‎ ‎ g·cm-3≈‎0.111 g·cm-3,由定义式可知,储氢能力=≈1 236。‎ 答案:(1)LaNi5　(2)‎ ‎(3)1 236‎ - 6 -‎